Akademik

в электродинамике- теорема, утверждающая, что поток вектора электрич. индукции D через замкнутую поверхность S пропорционален полному свободному заряду Q, заключённому внутри объёма V, охватываемого S. В Гаусса системе единиц:

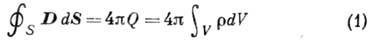
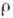(- объёмная плотность свободного заряда); в СИ множитель 4p отсутствует. Это соотношение получено К. Ф. Гауссом в 1830 для чисто эл.-статич. полей. Оно связано, по существу, с установленным ранее (1785) законом взаимодействия неподвижных электрич. зарядов - Кулона законом. Согласно (1), поле Е ₁ на расстоянии r₁ от точечного заряда q₁ в среде с пост. скалярной диэлектрич. проницаемостью равно E₁=, что и приводит к кулоновской ф-ле для силы взаимодействия F₁₂ двух точечных зарядов q₁ и q₂: 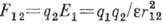. С помощью Гаусса - Остроградского формулы Г. т. можно записать в дифференц. форме:

В случае потенциального (напр., эл.-статич.) поля из ур-ния (2) в среде с постоянной е получается Пуассона уравнение . В 1864 Дж. К. Максвелл (J. С. Maxwell) постулировал (1) в качестве одного из фундам. ур-ний электродинамики [в традиц. нумерации, идущей от Г. Герца (H. Hertz) и О. Хевисайда (О. Heaviside), это четвёртое Максвелла уравнение], распространив тем самым Г. т. на случай переменных во времени полей.

Лит.:Tамм И. E., Основы теории электричества, 9 изд., M., 1976; Джексон Дж.. Классическая электродинамика, пер. с англ., M., 1965; Сивухин Д. В., Общий курс физики, 2 изд., [т. 3] - Электричество, M., 1983.

И. Г. Кондратьев, M А. Миллер.