Akademik

ЛИНЗА

ЛИНЗА: (нем. Linse, от лат. lens — чечевица), прозрачное тело, ограниченное двумя поверхностями, преломляющими световые лучи, способное формировать оптич. изображения предметов, светящихся собственным или отражённым светом. Л. явл. одним из осн. элементов оптич. систем. Наиболее употребительны Л., обе поверхности к-рых обладают общей осью симметрии, а из них — Л. со сферич. поверхностями, изготовление к-рых наиболее просто. Менее распространены Л. с двумя взаимно перпендикулярными плоскостями симметрии; их поверхности цилиндрич. или тороидальные. Таковы Л. в очках, предписываемых при астигматизме глаза, Л. для анаморфотных насадок и т. д.

Материалом для Л. обычно служит оптич. и органич. стекло. Спец. Л., предназначенные для работы в УФ области спектра, изготовляют из кристаллов кварца, флюорита, фтористого лития и др., в ИК — из особых сортов стекла, кремния, германия, флюорита, фтористого лития, йодистого цезия и др.

Описывая оптич. св-ва осесимметричной Л., чаще всего рассматривают лучи, падающие на неё под малым углом к оси, т. н. параксиальный пучок лучен.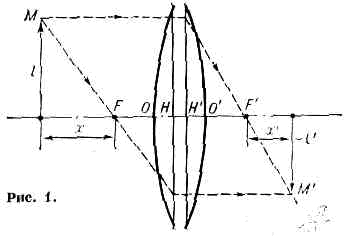

Действие Л. на эти лучи определяется положением её кардинальных точек — т. н, главных точек Н и Н', в к-рых пересекаются с осью главные плоскости Л., а также переднего и заднего главных фокусов F и F' (рис. 1). Отрезки HF=f и H'F'=f наз. фокусными расстояниями Л. (если среды, с к-рыми граничит Л., обладают одинаковыми показателями преломления, всегда f=f'); точки пересечения О и О' поверхностей Л. с осью наз. её вершинами, а расстояния между вершинами — толщиной Л. d.

Если направления фокусного расстояния совпадают с направлением лучей света, то его считают положительным, так, напр., на рис. 1 лучи проходят через Л. направо и так же ориентирован отрезок Н'F'. Поэтому здесь f'>0, а f0.

Л. изменяют направления падающих на неё лучей. Если Л. преобразует параллельный пучок в сходящийся, её называют собирающей; если параллельный пучок превращается в расходящийся, Л. называют рассеивающей. В главном фокусе F' собирающей Л. пересекаются лучи, к-рые до преломления были параллельны её оси. Для такой Л. f' всегда положительно. В рассеивающей Л. F' — точка пересечения не самих лучей, а их воображаемых продолжений в сторону, противоположную направлению распространения света. Поэтому для них всегда f'0. У тонких собирающих Л. толщина краёв меньше толщины в центре Л., у рассеивающих — наоборот.

Мерой преломляющего действия Л. служит её оптическая сила Ф — величина, обратная фокусному расстоянию (Ф=1/f') и измеряемая в диоптриях (м-1). У собирающих Л. Ф>0, поэтому их ещё именуют положительными, рассеивающие Л. (Ф0) называют отрицательными. Употребляют и Л. с Ф=0 — т. н. а ф о к а л ь н ы е Л. (их фокусное расстояние равно бесконечности). Они не собирают и не рассеивают лучей, но создают аберрации (см. АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ) и применяются в зеркально-линзовых (а иногда и в линзовых) объективах как компенсаторы аберраций.

Все параметры, определяющие оптич. св-ва Л., ограниченной сферич. поверхностями, могут быть выражены через радиусы кривизны r1 и r2 её поверхностей, толщину Л. по оси d и показатель преломления n её материала. Напр., оптич. сила и фокусное расстояние Л. задаются соотношением (верным лишь для параксиальных лучей) :

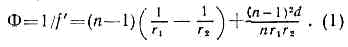Радиусы r1 и r2 считаются положительными, если направление от вершин Л. до центра соответствующей поверхности совпадает с направлением лучей (на рис. 1 r1=OF'>0, r2=O'F0). При одной и той же оптич. силе и том же материале форма Л. может быть различной. На рис. 2 показано неск. Л. одинаковой оптич. силы и разл. формы.

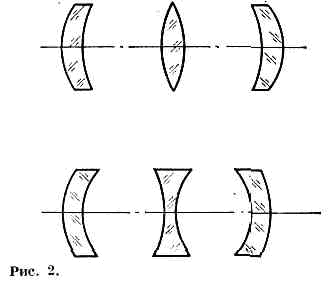Первые три — положительны, последние три — отрицательны. Л. наз. тонкой, если её толщина d мала по сравнению с r1 и r2. Достаточно точное выражение для оптич. силы такой Л. получают и без учёта второго члена в (1).

Положение гл. плоскостей Л. относительно её вершин (расстояния ОН и О'Н') тоже можно определить, зная r1, r2, n и d. Расстояние между главными плоскостями мало зависит от формы и оптич. силы Л. и приблизительно равно d(n-1)/n. В случае тонкой Л. это расстояние мало и практически можно считать, что главные плоскости совпадают.

Когда положение кардинальных точек известно, положение оптич. изображения точки, даваемого Л. (рис. 1), определяется ф-лами:

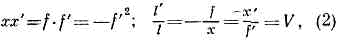где V — линейное увеличение Л. (см. УВЕЛИЧЕНИЕ ОПТИЧЕСКОЕ); l и l' — расстояния от точки и её изображения до оси (положительные, если они расположены выше оси); х — расстояние от переднего фокуса до точки; х' — расстояние от заднего фокуса до изображения. Если t и t' — расстояния от главных точек до плоскостей предмета и изображения соответственно, то

т. к. x=t-f, x'=t'-f')

f'/t'+f/t=1 или 1/t'-1/t=1/f'. (3)

В тонких Л. t и t' можно отсчитывать от соответствующих поверхностей Л.

Из (2) и (3) следует, что по мере приближения точки (действительного источника) к фокусу Л. расстояние от изображения до Л. увеличивается; собирающая Л. даёт действительное изображение точки в тех случаях, когда эта точка расположена перед фокусом; если точка расположена между фокусом и Л., её изображение будет м н и м ы м; рассеивающая Л. всегда даёт мнимое изображение действительной светящейся точки (подробнее см. в ст. (см. ИЗОБРАЖЕНИЕ ОПТИЧЕСКОЕ)).

ЛИНЗА

(нем. Linse, от лат. lens - чечевица) - простейший оптич. элемент, изготавливаемый из прозрачного материала, ограниченный двумя преломляющими поверхностями, имеющими общую ось либо две взаимно перпендикулярные плоскости симметрии. При изготовлении Л. для видимой области применяют оптическое стекло или органическое стекло (массовое тиражирование непрецизионных деталей), в УФ-диапазоне - кварц, флюорит и др., в ИК-диапазоне - спец. сорта стёкол, кремний, германий, сапфир, ряд солей и т. д.

Рабочие поверхности Л. обычно имеют сферич. форму, реже - цилиндрическую, тороидальную, конусообразную или с заданными небольшими отступлениями от сферы (асферическую). Л. со сферич. поверхностями наиб. просты в изготовлении и являются осн. элементами большинства оптич. систем.

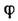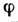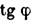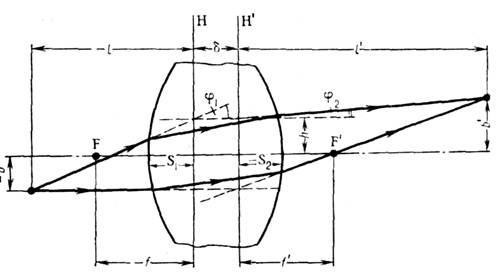
В параксиальном приближении (углы между лучами и оптич. осью столь малы, что можно заменить sinи на 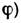свойства Л. со сферич. поверхностями могут быть однозначно охарактеризованы положением главных плоскостей и оптической силой Ф, представляющей собой выражаемую в диоптриях величину, обратную фокусному расстоянию (в м). Связь этих характеристик с геом. параметрами Л. ясны из рис., в к-ром для наглядности углы наклона лучей изображены преувеличенно большими. Расстояния от первой по ходу лучей поверхности линзы до первой гл. плоскости Я и от второй поверхности до второй гл. плоскости H' равны соответственно

S_{1, 2}

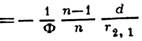
фокусное расстояние от H до переднего фокуса (F)f= -1/Ф, от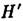 до заднего фокуса I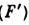 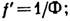оптич. сила Л., являющаяся мерой её преломляющего действия, равна

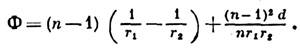
Здесь п - показатель преломления вещества Л. (или отношение этого показателя к показателю преломления окружающей среды, если последний 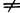1), d - измеренная вдоль оси толщина Л., r₁ и r₂ - радиусы кривизны её поверхностей (считаются положительными, если центры кривизны расположены дальше по ходу лучей; так, у изображённой на рис. двояковыпуклой Л. r₁>0, r₂<0), расстояния отсчитываются вдоль направления распространения света.

Способ построения и расчёта траекторий проходящих через Л. меридиональных (лежащих в осевой плоскости) лучей с использованием гл. плоскостей ясен из рис. После прохождения Л. луч кажется исходящим из точки на 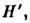удалённой от оси на то же расстояние h, что и точка пересечения исходного луча с Я. Угол между лучом и осью изменяется на 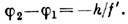Для нахождения траектории произвольного немеридионального луча последний проецируется на две взаимно перпендикулярные осевые плоскости. Каждая проекция является по существу меридиональным лучом и ведёт себя указанным выше образом.

Положение даваемого Л. изображения точки определяется ф-лами

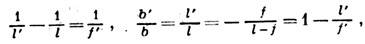
где l и 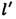- расстояния от гл. плоскостей до плоскостей предмета и изображения соответственно (рис.), b и 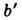- расстояния точки и её изображения от оси (отсчитываемые вверх).

Если 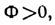Л. наз. положительной или собирающей, при 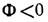- отрицательной или рассеивающей; линзы с Ф=0 наз. афокальными и используются гл. обр. для исправления аберраций др. оптич. элементов. Положительные Л. дают действительные изображения всех действительных объектов, находящихся до переднего фокуса (на рис.- левее F), и всех мнимых объектов, находящихся за Л. Рассеивающие Л. дают расположенное между Л. и передним фокусом прямое, мнимое, уменьшенное изображение действит. объектов.

Расстояние 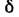между гл. плоскостями Л. почти не зависит от её оптич. силы и формы и примерно равно d(1-1/n). Когда 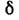пренебрежимо мало по сравнению с 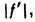Л. наз. тонкой. У тонких Л. знак оптич. силы Ф совпадает со знаком разности 1/r₁-1/r₂; при этом толщина собирающих Л. по мере удаления от оси уменьшается, а рассеивающих - возрастает. Обе гл. плоскости тонких Л. можно считать совпадающими с плоскостью Л. и отсчитывать введённые выше расстояния /, 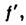l,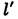прямо от последней. Чёткой границы между толстыми Л. (когда 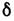нельзя пренебречь) и тонкими не существует - всё зависит от конкретных применений.

Для преобразования высококогерентных световых пучков (обычно лазерного происхождения) используются преим. тонкие Л. Их часто наз. квадратичными фазовыми корректорами: при прохождении когерентного пучка через тонкую Л. к распределению фазы по его сечению добавляется величина 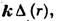где k= 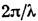- волновой вектор, 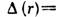= ( п-1) 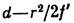- вносимая Л. дополнит. разность хода, являющаяся квадратичной ф-цией удаления r от оси. Распределение комплексной амплитуды поля в фокальной плоскости Л. с точностью до фазового множителя является фурье-образом распределения амплитуды поля перед Л., вычисленным для пространственных частот 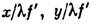(х, у - поперечные координаты на фокальной плоскости). Распределение интенсивности в той же плоскости подобно угл. распределению излучения с коэф. подобия 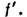Поэтому Л. широко применяются в системах пространственной фильтрации излучения, обычно представляющих собой комбинацию Л. с установленными в их фокальных плоскостях диафрагмами, растрами, и в устройствах для измерения угл. расходимости излучения.

Л. обладают всеми аберрациями, присущими цент-риров. оптич. системам (см. Аберрации оптических систем). Проблема аберраций особенно важна при использовании широкополосных и обладающих большими угл. апертурами световых пучков обычных (некогерентных) источников. Сферич. и хроматич. аберрации, а также кома могут быть в значит. степени исправлены путём комбинирования двух Л. разл. формы и из материалов с разл. дисперсией. Такие двухлинзовые системы широко используются в качестве объективов для зрительных труб и т. п. Иногда сферич. аберрации уничтожаются с помощью Л. с асферической, в частности параболоидальной, формой поверхности.

Для коррекции разл. дефектов глаза применяются Л. не только со сферическими, но также с цилиндрич. и торич. поверхностями. Цилиндрич. Л. сравнительно часто используются в тех случаях, когда изображение точечного источника должно быть "растянуто" в полосу или линию (напр., в спектральных приборах).

Лит.: Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973; Гудмен Д ж., Введение в Фурье-оптику, пер. с англ.. М.. 1970. Ю. А. Ананьев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.