Akademik

FONCTIONS ANALYTIQUES

DEPUIS l’Antiquité, on connaît en substance la série géométrique suivante:

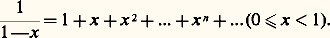
Une des grandes découvertes qui jalonnèrent la formation du calcul infinitésimal au milieu du XVII^e siècle fut la possibilité de représenter les fonctions «usuelles» (logarithme, exponentielle, fonctions trigonométriques, etc.) par des développements en série analogues. Au XVIII^e siècle, la plupart des mathématiciens en étaient arrivés à ne plus guère considérer comme dignes d’intérêt que les fonctions dites «analytiques», égales à la somme d’une série convergente du type:

au voisinage de chacun des points x ⁰ de leur domaine d’existence.

La plupart des fonctions considérées au XVIII^e siècle étaient implicitement supposées analytiques, et J. L. Lagrange, dans sa Théorie des fonctions analytiques (1797), tente de fonder une théorie formelle de la dérivation, indépendante de la notion d’infiniment petit ou de limite, sur le concept de développement en série entière.

Si, depuis le début du XIX^e siècle, il a fallu abandonner ce point de vue trop exclusif, et donner droit de cité à des fonctions bien moins «régulières» que les fonctions analytiques, le rôle de ces dernières reste fondamental dans toutes les parties des mathématiques. En fait, le concept d’analyticité s’est même élargi depuis le début du XX^e siècle; la définition d’une série entière:

et le calcul sur ces séries gardent en effet un sens lorsque les coefficients c ⁿ et la variable x ne sont plus nécessairement des nombres réels ou complexes, mais plus généralement appartiennent à un corps valué complet , par exemple le corps des nombres p -adiques (cf. théorie des NOMBRES – Nombres p -adiques): il ne s’agit pas là d’une généralisation sans motivation, car ce qu’on appelle maintenant l’analyse p-adique a pris dans ces dernières années une importance de plus en plus grande dans toutes les questions touchant la théorie des nombres algébriques (cf. théorie des NOMBRES – Nombres algébriques).

Toutefois, une étude plus poussée révèle que la possibilité de donner une définition de la notion de «fonction analytique» sur un corps valué complet quelconque K masque en réalité de profondes différences de comportement pour ces fonctions, selon la nature du «corps de base» K considéré. Déjà, entre le cas réel (K = R) et le cas complexe (K = C), il y a un clivage abrupt, la théorie des fonctions analytiques de variables complexes étant incomparablement plus riche et plus simple que celle des fonctions analytiques de variables réelles (cf. représentation et approximation des FONCTIONS, chap. 1): pour ne citer qu’un exemple, la seule existence de la dérivée première pour une fonction d’une variable complexe la rend ipso facto analytique. La raison de cette différence doit être cherchée dans la théorie de Cauchy , fondée sur le merveilleux outil que constitue l’intégrale curviligne des fonctions de variable complexe, d’une souplesse et d’une puissance incomparables.

C’est seulement de cette théorie et de ses extensions qu’il est question dans les articles qui suivent. Jusqu’à la fin du XIX^e siècle, on ne s’est guère occupé que de la théorie des fonctions d’une seule variable complexe, qui offrait aux recherches un champ aussi vaste que riche (d’ailleurs loin d’être épuisé même à l’époque actuelle): en dehors de ses innombrables applications dans toute l’analyse, la théorie de Cauchy rejoignait la géométrie différentielle par ses liens avec la représentation conforme et les surfaces minimales, la théorie du potentiel (en mathématiques et en physique) par ses étroites relations avec les fonctions harmoniques de deux variables, et (ce qui est sans doute le plus inattendu) l’arithmétique supérieure avec la théorie analytique des nombres (séries de Dirichlet, méthode de Hardy-Littlewood).

Les conceptions les plus profondes qui se font jour pendant cette période sont celles de Riemann, qui parvint à maîtriser les difficultés que créaient depuis Bernoulli et Euler les prétendues «fonctions multiformes» par l’invention géniale des «surfaces de Riemann», premier exemple de ce que l’on appelle maintenant les «variétés holomorphes», et point de départ de la topologie moderne. La nécessité d’admettre comme domaines de définition des fonctions holomorphes des variétés plus générales que les ouverts des espaces Cⁿ devait apparaître avec encore plus de netteté dans les études sur les fonctions de plusieurs variables complexes. Cette étude ne commença guère qu’au début du XX^e siècle; dès les premiers travaux sur la question, on se rendit compte des différences profondes qui la distinguaient de la théorie des fonctions d’une seule variable complexe, qui apparaît maintenant comme un cas d’exception; de ce fait, il fallut forger de nouveaux moyens d’attaque, qui ont surtout été l’œuvre de H. Cartan et K. Oka dans les années 1930-1955. La tournure essentiellement géométrique qu’a prise cette théorie lui vaut le nom amplement justifié de géométrie analytique sous lequel on la désigne aujourd’hui, et la rapproche étroitement de la géométrie algébrique moderne: le parallélisme des énoncés dans ces deux théories est tout à fait remarquable, mais les méthodes de démonstration sont en général très différentes, et beaucoup plus délicates pour la géométrie analytique.

Les liens entre la théorie des fonctions analytiques et la géométrie algébrique remontent d’ailleurs beaucoup plus haut, avec la théorie des fonctions elliptiques et des intégrales abéliennes, qui constituèrent dans la première moitié du XIX^e siècle un des triomphes de la théorie de Cauchy et furent au centre des recherches de Riemann. La théorie des fonctions elliptiques conduisit un peu plus tard à l’étude de la fonction modulaire, premier exemple des fonctions automorphes d’une variable complexe, brillamment développée par Felix Klein et surtout Henri Poincaré. Par là même, la théorie des fonctions analytiques entrait en contact avec la théorie des groupes; les rapports entre ces théories sont devenus encore plus étroits à l’époque moderne, lorsque Siegel, en généralisant aux fonctions de plusieurs variables complexes la notion de fonction automorphe, a placé la théorie de ces dernières dans ce qui semble son cadre naturel, la théorie des espaces symétriques d’Élie Cartan.