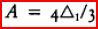because any value of A unequal to 4Δ1/3 can be refuted by
summing sufficiently many triangles Δ1,…,Δn. The method ‘exhausts all possibilities’
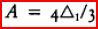except and, more importantly, each incorrect possibility is eliminated by
reasoning about the finite sum of Δ1,…,Δn.
Figure 1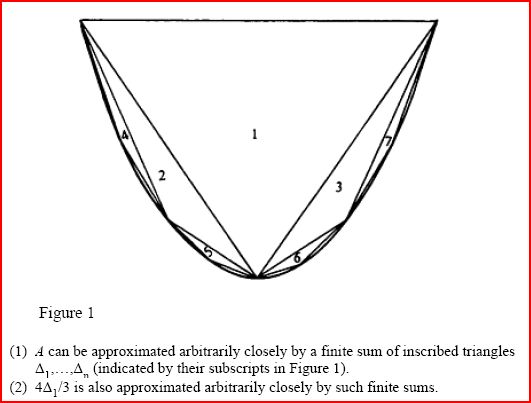 
The theory of proportions and the method of exhaustion enabled mathematicians to
sidestep their first encounter with infinity. It was not necessary to sum infinitely many
triangles to determine A, for example; the sum of Δ1,…,Δn was sufficient, provided n was
arbitrary. One might say that infinity is present in the arbitrariness of n, but only
‘potentially’ so. The Greeks (and most mathematicians until the nineteenth century) drew
a sharp distinction between the potential infinity which supplies natural numbers one by
one, and the actual infinity which delivers them all at once. The concept of natural
number is in fact potential infinity in a nutshell; the process of beginning with 0 and
adding 1 ‘indefinitely’ is what the natural numbers are all about. The idea that this
process could ever be completed seems at first as unnatural and uncalled for as a last
natural number.
However, the distinction between potential and actual infinity is not so easy to
maintain in other cases. Consider the following example. To travel a distance of one
kilometer, say, one first has to reach the 0.9 kilometer mark, then the 0.99 kilometer
mark, then the 0.999 kilometer mark…, and in general the 1–1/10n kilometer mark for
each n. One seemingly cannot complete the journey without also completing the infinity
of values 1–1/10n. A similar example is discussed in Aristotle’s Physics, 239b, 14, under
the name of Zeno’s paradox of Achilles and the tortoise. Aristotle refutes it by appealing
to the (potentially) infinite divisibility of space and time. The kilometer can be
subdivided at 0.9, 0.99, 0.999,…and the time interval required for the journey can be
subdivided similarly, so completion of the journey involves only the potential infinity of
subdivisions.
We do not know the purpose of Zeno (c. 450 BC) in formulating his paradoxes, since
they are known to us only through Aristotle, who wished to debunk them. Nevertheless,
Zeno does seem to have put the fear of infinity into Greek mathematics. It is otherwise
hard to understand the rejection of irrational numbers, and the restriction to potential
infinity even in cases where actual infinity seems harmless. We now know, in fact, that
Archimedes used actual infinity to discover his results on areas and volumes. His original
methods were uncovered only in 1906, thanks to some extraordinary detective work by
Heiberg ([9.26], 5). By then, it was too late for them to have any effect on mathematical
practice.
After the classical era, the next major encounter with infinity was in the seventeenth
century. The occasion was the invention of the calculus, a resurgence of Archimedes’
theory of curved figures powered by the new algebraic geometry of Fermat and
Descartes. Algebra made an enormous difference to geometry. Whereas Archimedes had
to make an ingenious new approach to each new figure—for example, the approach to the
parabolic segment using specially placed triangles—calculus dealt with a great variety of
figures in the same way, via their equations. That was the whole point. Calculus was a
method of calculating results, rather than proving them. If pressed, mathematicians could
justify their calculations by the method of exhaustion, but it seemed impractical if not
unnecessary to do so. Even before the stream of new results reached full flood with
Newton and Leibniz (from 1665 onward) Huygens had warned:
Mathematicians will never have enough time to read all the discoveries in
Geometry (a quantity which is increasing from day to day and seems likely in
this scientific age to develop to enormous proportions) if they continue to be
presented in a rigorous form according to the manner of the ancients.
([930], 337)
In fact, Huygens was probably the only major mathematician who stuck to the ‘methods
of the ancients’. The methods of calculus were so much more powerful and efficient that
rigour became secondary. Hobbes and Berkeley wrote scathing attacks on the illogical
language of ‘infinitesimals’ used by mathematicians as a substitute for exhaustion, but
they could not deny that it got results. And what results! By the middle of the eighteenth
century, calculus had solved almost all the problems of classical geometry, and new ones
the ancients had not dreamed of. It had also revealed the secrets of the heavens,
explaining the motions of the moons and planets with uncanny precision. Apart from a
few marginal controversies over such things as the infinite series 1−1+1−1+…, all the
results of calculus stood up to rigorous scrutiny.
The confidence inspired by the success of calculus was infectious. During the
eighteenth century, mathematicians pushed their luck even further, using some concepts
they did not know how to justify. They freely used √-1 while calling it ‘imaginary’ or
‘impossible’. They assumed that arbitrary continuous functions were expressible as
infinite sums of sine waves. And once again their faith was rewarded, with an avalanche
of new discoveries in mathematics and physics by d’Alembert, the Bernoullis, Euler and
Lagrange. With this much success, mathematicians could afford to ignore philosophical
questions about the meaning and rigour of their work. Only a direct contradiction in the
heart of mathematics could give them pause. When it came, all the forgotten fears of
irrationality and infinity would come back to the surface.
THE CRISIS IN GEOMETRY
Before 1800, geometry was thought to be part of physics. Its simplest elements—straight
lines and circles—were idealizations of the simplest physical curves, constructed by the
simplest drawing instruments, the straight edge and compasses. However, what set
geometry apart from the rest of physics was its logical structure. It appeared that all
properties of straight lines and circles (in the plane) were logical consequences of five
axioms postulated by Euclid in his Elements (c. 300 BC):
Let the following be postulated
1. To draw a straight line from any point to any point.
2. To produce a finite straight line continuously in a straight line.
3. To describe a circle with any centre and distance.
4. That all right angles are equal to one another.
5. That, if a straight line falling on two straight lines make the interior angles on the
same side less than two right angles, the lines, if produced indefinitely, meet on that
side on which are the angles less than the two right angles.
([9.27], 154)
Euclid’s axioms were physically plausible, at least within the limits of measurement
possible before 1800, though of course the fifth axiom could not be tested properly with
finite lines. What was more important, in the opinion of most mathematicians and
philosophers, was that no alternatives to Euclid’s axioms could be imagined. In
particular, it seemed impossible to imagine either of the following alternatives to axiom
5:
5+. Two straight lines, if produced indefinitely, meet on both sides.
5−. There are straight lines which fail to meet even though a straight line falling on them
makes interior angles on the same side less than two right angles. (Or the following
logical equivalent: given a line L and point P not on L there is more than one line
through P not meeting L.)
The strongest statement of the a priori nature of geometry was made by Kant in his
Critique of Pure Reason. Kant believed that the fact that we cannot imagine alternatives
such as 5+ and 5− made Euclid’s geometry the only one logically possible or meaningful:
It is therefore, solely from the human standpoint that we can speak of space, of
extended things, etc. If we depart from the subjective condition under which
alone we can have outer intuition, namely, liability to be affected by objects, the
representation of space stands for nothing whatsoever.
([9.31], 71)
Kant’s philosophy was the high-water mark of intuitive geometry. The tide turned during
the nineteenth century when mathematicians became increasingly absorbed with the
construction of geometries contradicting Euclid, and later with the reconstruction of
Euclidean geometry itself.
These investigations stemmed from dissatisfaction with Euclid’s axiom 5, the so-called
parallel axiom. Gauss, Bolyai and Lobachevsky realized that it was impossible to
confirm the parallel axiom by physical experiment, and in fact conceivable that one could
refute it. This was because the parallel axiom has the consequence that the angle sum (in
radians) of any triangle is π. Since perfectly accurate measurement is impossible, one
could never be sure that an angle sum measured to be π was in fact equal to π; and
conceivably a triangle could be found with angle sum definitely not equal to π, i.e.
differing from π by more than experimental error. While no physical refutation of the
parallel axiom succeeded at the time (success was not achieved until 1919, as part of the
confirmation of general relativity theory) its very possibility was enough to encourage
Gauss, Bolyai and Lobachevsky to explore an alternative to Euclidean geometry. Their
investigations were made independently, roughly between 1800 and 1830, and reached
similar conclusions.
Each of them studied the replacement of the parallel axiom by the axiom 5−. The
geometry that results from this replacement is now called hyperbolic geometry. It is in
some ways more complicated than Euclidean geometry. For example, there are no similar
figures of different sizes. There are no squares. Equilateral triangles of different sizes
have different angles (always less than the angle π/3 of a Euclidean equilateral triangle).
However, in other ways hyperbolic geometry is extremely elegant and convenient. The
fact that equilateral triangles of different sizes have different angles yields an absolute
unit of length. One could define the unit to be, say, the side of the equilateral triangle with
angle π/4, since there is only one size of equilateral triangle with this angle. Likewise,
the fact that the angle sum of a triangle is less than π makes it possible to show that the
area of a triangle is proportional to the difference between π and the triangle’s angle
sum. Thus, in hyperbolic geometry, area can be measured by angles.
These beautiful consequences of axiom 5−, and the non-appearance of any
contradictory consequences, convinced Gauss, Bolyai and Lobachevsky that hyperbolic
geometry was meaningful and worth pursuing. However, there was no immediate threat
to the authority of Euclid and Kant. Gauss was too afraid of controversy to publish his
results. Bolyai gave up soon after publication of his work in 1832, discouraged by the
lack of response from other mathematicians and troubled by the possibility that
contradictions might yet emerge. Lobachevsky published doggedly from the obscurity of
Kazan from 1829 until 1856, the year of his death, without any encouragement from the
outside world. (Gauss in fact admired Lobachevsky’s work, but communicated his
feelings only to his friend Schumacher in a letter [9.24].
But in 1855 Gauss died, and his interest in hyperbolic geometry became known to the
mathematical world through the release of his unpublished papers. This led to a more
widespread interest in hyperbolic geometry, particularly in the light of differential
geometry, a field also pioneered by Gauss with his book on curved surfaces [9.23], and
invigorated by the ideas of Riemann [9.38] on curved space of arbitrary dimensions.
On any smooth surface there are curves called geodesics which are ‘as straight as
possible’ and hence can be regarded as the ‘lines’ of a ‘geometry’. On the sphere, for
example, the geodesics are the great circles, because a great circle gives the shortest
distance between any two points on the sphere. The corresponding ‘geometry’ is
spherical geometry, which studies such things as spherical triangles. Spherical geometry
had in fact been studied since ancient times because of its applications to astronomy and
navigation, but the idea of its being a ‘geometry’ with theorems contrary to those of
Euclidean geometry had not come up, perhaps because its ‘lines’ are manifestly finite and
closed.
However, the curved ‘lines’ on the sphere can be made straight by projecting the
sphere from its centre on to a tangent plane (Figure 2). Admittedly, only half of each
spherical ‘line’ can be seen at a time this way, and spherical distance becomes distorted.
However, it does make spherical geometry look like a geometry of genuine lines, and it
raises an interesting question. For which surfaces is there a map to the plane carrying
geodesics to straight lines?
Figure 2 
Beltrami [9.2] found the answer in terms of the curvature of the surface, a concept
introduced in Gauss [9.22]. The surfaces whose geodesics can be mapped to straight lines
are precisely those of constant curvature. The plane itself is of zero curvature, a sphere
has constant positive curvature—which explained the known examples—but there are
also surfaces of constant negative curvature. The first of these to be discovered was the
pseudosphere, a trumpet-shaped surface (Figure 3) whose geometry had been
investigated by Gauss’s student Minding in 1840. Minding even made the pregnant
discovery that its triangles are governed by formulas like those for spherical triangles, but
with the circular functions sine and cosine replaced by their hyperbolic analogues sinh
and cosh (hence the name ‘pseudosphere’). The same formulas had already been found to
hold in hyperbolic geometry by Lobachevsky [9.34].
Figure 3 
Unfortunately the pseudosphere cannot be regarded as a complete
realization of hyperbolic geometry, because ‘lines’ on the pseudosphere do not extend
indefinitely. The rim of the trumpet is an impassable boundary, beyond which the
pseudosphere cannot be extended because its curvature becomes undefined there. In 1868
Beltrami [9.3] saw a way round this difficulty with his mapping of geodesics to straight
lines. The pseudosphere is mapped on to a portion of the disc (Figure 4) and the line
segments representing its geodesics have a natural exten-
sion to the whole interior of the disc. (The boundary of the disc is infinitely far away, in
the sense of distance on the pseudosphere. In particular, the point E represents the
infinitely distant end of the trumpet.) Thus the whole interior of the disc has a geometry,
inherited from the pseudosphere, and it is the complete hyperbolic geometry of Gauss,
Bolyai and Lobachevsky. The validity of the hyperbolic parallel axiom 5− is particularly
clear, as Figure 5 shows.
Figure 4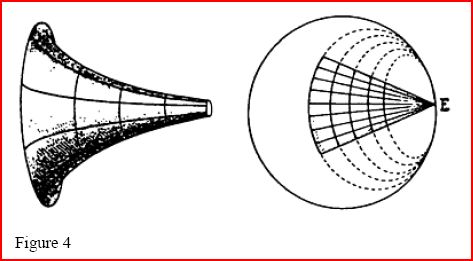 
Figure 5 
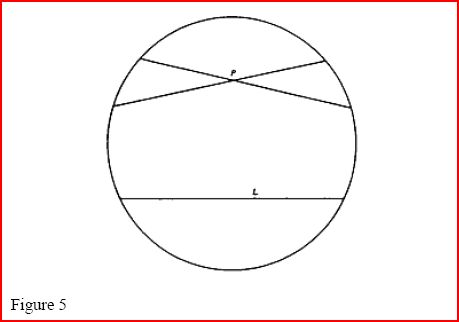Beltrami had found what we now call a model of hyperbolic geometry—an
interpretation of the terms ‘point’, ‘line’, etc. within Euclidean geometry under which the
axioms 1, 2, 3, 4, 5− are satisfied.
It follows that the Gauss-Bolyai-Lobachevsky axioms cannot lead to a contradiction,
unless there is a contradiction in Euclidean geometry itself. This was Beltrami’s great
contribution to the philosophy of geometry. As he put it (rather modestly) in his 1868
paper:
In recent times the mathematical public has begun to take an interest in some
new concepts which seem destined, if they prevail, to change profoundly the
whole complexion of classical geometry.
These concepts are not particularly recent. The master Gauss grasped them at
the beginning of his scientific career, and although his writings do not contain
an explicit exposition, his letters confirm that he had always cultivated them and
attest to his full support for the doctrine of Lobachevsky.
…we have sought, to the extent of our ability, to convince ourselves of the
results of Lobachevsky’s doctrine; then, following the tradition of scientific
research, we have tried to find a real substrate for this doctrine, rather than
admit the necessity for a new order of entities and concepts. We believe we
have attained this goal for the planar part of the doctrine.
(Beltrami 1868 in [9.17], 533)
Beltrami’s model showed that Euclid’s axioms 1, 2, 3, 4, 5 are not the only logical
possibility. It was therefore admissible to doubt that they were true of physical space.
If Euclid’s geometry was not about physical space, what was it about?
ARITHMETIZATION
With the discovery of non-Euclidean geometry the nature and existence of geometric
objects was called into question. It was time to take up an option which had been
available for two centuries, but held back out of respect for the Greek tradition of
separating the concepts of number and length—the arithmetization of geometry. Around
1630, Fermat and Descartes independently discovered the method of co-ordinates which
makes it possible to describe curves by equations in variables x and y. Given two lines OX
and OY in the plane (Figure 6), any point P is determined by its distances x and y from
them. (It is convenient, though not necessary, to take OX and OY to be perpendicular, and
to let y and x be the perpendicular distances from P to them.) As P traverses a curve in the
plane, x and y enter a certain relationship, which Fermat and Descartes found they could
easily describe in many important cases.
Figure 6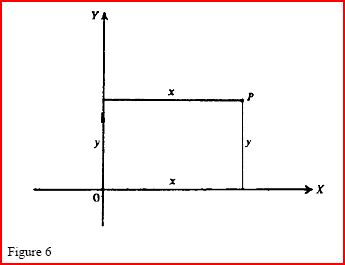 
For example, if P describes the straight line passing through O and equidistant from OX
and OY, then y=x. More generally, any straight line is described by an equation of the
form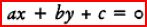 
where a, b, c are constants,
and which we now call a linear equation for that reason. Conversely, any such
equation (provided a, b are not both zero) represents a straight line, so there is a
correspondence between lines and linear equations.
Linear equations are recognizable algebraically as those in which x and y occur to the
first power. The next simplest equations, called quadratic, include terms in x2, y2 and xy
as well as linear terms. Fermat and Descartes discovered that the curves described by
quadratic equations are precisely the conic sections (ellipses, parabolas, hyperbolas),
which had been studied by the Greeks, particularly by Apollonius, c. 200 BC. Apollonius
even knew the relationship between x and y for a conic section, but he expressed it in
words (taking about half a page!) and not as an equation. Lacking algebraic notation, the
Greeks could hardly form the idea of equations, let alone manipulate them so as to be
able to recognize the curves they described. Fermat and Descartes had the advantage of a
well developed notation and technique for algebra, thanks to the efforts of their
compatriot Viète (1540–1603) and the Italians del Ferro, Tartaglia, Cardano,
Ferrari and Bombelli in the sixteenth century. In turn, Descartes’ Geometry (1637,
[9.15]) made a big impression on Newton, who carried the analysis of equations beyond
the range of classical geometry with a classification of cubic curves [9.37]. Thus by the
end of the seventeenth century it was well established that curves could be studied by
algebra, at least the curves expressed by polynomial equations, i.e. equations formed by
applying arithmetic operations to x and y.
However, these developments did not prompt any reassessment of the nature of curves.
No one said that curves were equations. Moreover, the variables x and y were regarded as
lengths rather than numbers. Thanks to Eudoxus’ theory of proportions (see Introduction
above), x and y could be regarded as lengths while only arithmetic operations were
applied to them, so the Greek segregation of geometry from number remained in force.
The inadequacies of the theory of proportions (and indeed the theory of numbers) were
not exposed until questions about curves in general began to be asked in the eighteenth
century. Perhaps the turning point was Gauss’s proof of the fundamental theorem of
algebra [9.22].
The exact statement proved by Gauss does not concern us here (the modern equivalent
is that any polynomial equation has a solution in the complex numbers). The point of
interest is the following statement assumed by Gauss in his proof. If K1 and K2 are curves
inside a circle, and the endpoints A1, B1 of K1 separate the endpoints A2, B2 of K2 on the
circle (Figure 7), then K1 and K2 have a common point. The only justification Gauss
offered for this statement was that ‘no one, to my knowledge, has ever doubted it’. This
was probably true, but
Figure 7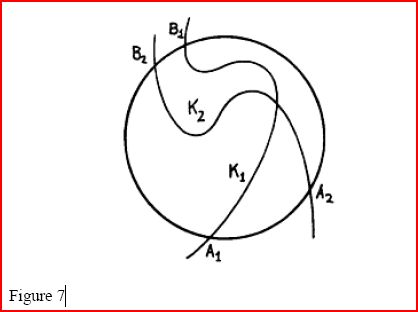 
nevertheless a poor excuse, particularly since Gauss was well aware of gaps in previous
attempts to prove the fundamental theorem, and at pains to point them out. Quite likely,
the only reason the statement had never been doubted is that it had never previously been
used in a mathematical proof. Gauss’s proof was probably the first existence proof in the
history of mathematics—one where the existence of a point was proved without a means
of constructing it—and probably the first to use topological reasoning. The basic concept
of topology, namely continuity, had not even been defined in 1799, and Gauss’s claim is
not easy to prove even when the notion of continuous curve has been made clear.
It seems that Gauss realised the seriousness of the gap in his proof, because in 1816 he
offered another proof of the fundamental theorem of algebra in which the role of
continuity was minimized. In his second proof he assumed only that if p(x) is a
polynomial such that 
for some real numbers a and b then p(c)=o for
some c between a and b. This assumption, known as the intermediate value theorem (for
polynomials) can be viewed as a special case of the assumption in the first proof, namely,
where K1 is part of OX and K2 is part of the curve y=p(x) (Figure 8).
Figure 8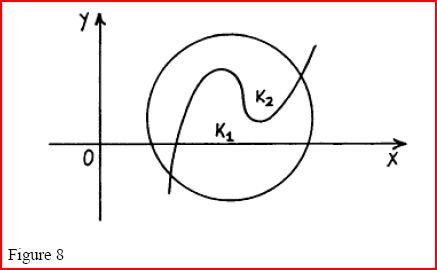 
The intermediate value theorem is needed even to show the existence of 
, which is the
value for which 
becomes zero between, say, x=1 and x=2. Thus any
proof of the fundamental theorem of algebra involves the intermediate value theorem, at
least implicitly.
This point was recognized by Bolzano in 1817 [9.5], immediately after the appearance
of Gauss’s proof. Bolzano gave a proof of the continuity of polynomial curves y=p(x),
and attempted a proof of the intermediate value theorem for arbitrary continuous curves
y= f(x). His definition of continuity was essentially the modern one:
a function fx varies according to the law of continuity for all values of x inside
or outside certain limits means just that: if x is some such value, the difference
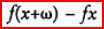can be made smaller than any given quantity provided ω can
be taken as small as we please.
(Bolzano 1817 in [9.17], 565)
However, his proof of the intermediate value theorem assumes the following least upper
bound property of real numbers:
whenever a certain property M belongs to all values of a variable quantity i
which are smaller than a given value and yet not for all values in general, then
there is always some greatest value u, for which it can be asserted that all i<u
possess property M
([9.17], 565)
Actually, the value u is greatest lower bound of the values not having property M. It is
now more usual to consider the equivalent least upper bound property: every bounded set
of real numbers has a least upper bound. Bolzano was unable to prove this property
rigorously because he did not have a definition of real number. Nevertheless, identifying
the property was an important step. It set a requirement that any future definition of real
number would have to meet, and was the first indication that further clarification of
geometric concepts would depend on clarification of the concept of number.
WHAT IS A REAL NUMBER
In 1858, the last student of Gauss, Richard Dedekind, found himself teaching elementary
calculus at the Polytechnic School in Zurich. He later wrote:
In discussing the notion of the approach of a variable magnitude to a fixed
limiting value, and especially in proving the theorem that every magnitude
which grows continually, but not beyond all limits, must approach a limiting
value, I had recourse to geometric evidences. Even now such resort to geometric
intuition… I regard as exceedingly useful… But that this form of introduction
into the differential calculus can make no claim to being scientific, no one will
deny.
([9.14], 1)
Dedekind, too, had glimpsed the elusive least upper bound property. He was determined
to capture it.
I made the fixed resolve to keep meditating on the question until I should find a
purely arithmetic and perfectly rigorous foundation for the principles of
infinitesimal analysis. The statement is so frequently made that the differential
calculus deals with continuous magnitude, and yet an explanation of this
continuity is nowhere given; even the most rigorous expositions of the
differential calculus do not base their proofs on continuity…they either appeal
to geometric notions…or depend upon theorems which are never established in
a purely arithmetic manner. Among these, for example, belongs the abovementioned
theorem, and a more careful investigation convinced me that this
theorem, or any one equivalent to it, can be regarded in some way as a sufficient
basis for infinitesimal analysis
([9.14], 7)
Having seen clearly what the difficulty was: ‘It then only remained to discover its true
origin in the elements of arithmetic and thus at the same time to secure a real definition of
the essence of continuity. I succeeded Nov. 24, 1858’ ([9.14], 2).
What then was Dedekind’s definition that captured the essence of continuity? In a
nutshell, it was what Eudoxus would have said if he had believed in actual infinity. Like
Eudoxus, Dedekind determined a length by comparison with rational numbers, but,
unlike Eudoxus, Dedekind considered the totality of rational numbers to be an actual
object—a set—and he declared the length being determined to be a number.
The length √2, for example, is greater than a positive rational m/n if and only if
2n2>m2, as we observed in the Introduction above. This gives a numerical process for
comparing m/n with √2, essentially Eudoxus’ theory of proportions. Dedekind sought a
numerical object he could identify with √2, and found it in the completed outcome of
the comparison process, namely the pair of sets of positive rationals
\m/n : 2n2 < m2 and \m/n:2n2 > m2
In general, Dedekind defined a real number to be a partition of the rationals into two
sets A1, A2 such that each member of A1 is less than every member of A1. He called such
a partition a cut. Each rational number r itself produces a cut, or rather two cuts (one with
r the maximum member of A1, the other with r the minimum member of A2), so the
rationals are naturally absorbed into this more comprehensive concept of number. The
real numbers also inherit natural operations of sum, product, etc. from the rational
numbers. For example, if α is the cut (A1, A2) and (β is the cut (B1, B2) then α + β is
the cut (C1, C2), where C1 is the set of sums a1+b1 where a1 is in A1 (i.e. a1 < α) and
b1 is in B1 (i.e. b1 < β), and C2 consists of the rationals not in C1. In this way it
becomes possible to prove results such as √2√3=√6, which Dedekind believed
had not been proved rigorously before. (It would, however, have been possible to prove
√2√3=√6 rigorously for lengths √2√3=√6 by the theory of proportions.)
Finally, it was easy to prove the least upper bound property. If a real quantity α grows
continually but not beyond a limit β say, consider the set L1 of all rationals belonging to
lower sets A1 of values of α. Then if L2 is the set of rationals not in L1 (in particular L2
includes the rationals greater than β) it is easily seen that (L1, L2) is a cut and it is the
least upper bound of the variable quantity α.
The least upper bound property is one of several equivalent statements of what
Dedekind called the continuity of the real numbers (nowadays called the completeness of
the real numbers). Another is that there is no gap, that is, no partition of the real numbers
into sets A1, A2 with each member of A1 less than every member of A2, no maximum
member of A1 and no minimum member of A2. This property is an almost immediate
consequence of Dedekind’s definition, which essentially fills each gap in the rational
numbers by a real number.
As Dedekind pointed out, the continuity of the real numbers enables them to serve as a
model of points on the line. Thus the key step in the arithmetization of geometry was
finally achieved. With the line defined as the set of real numbers x, it is natural to define
the plane as the set of ordered pairs of real numbers, (x, y), and then curves can be
defined by equations in x and y. This programme was completed in the Grundlagen der
Geometrie of Hilbert (1899, [9.26]). Incidentally, the pair (x, y) is also used as a concrete
representative of the complex number x+y√-I, thus giving a meaning to
‘imaginary’ numbers (see Introduction above).
In the meantime, several other definitions of real number had been proposed, notably
by Meray [9.32], Weierstrass [9.29] and Cantor [9.9]. Weierstrass [9.37] also gave the
first rigorous proofs of the fundamental theorems on continuous functions, in particular
the intermediate value theorem anticipated by Bolzano [9.5]. Meray, Weierstrass and
Cantor all defined real numbers as sets of convergent infinite sequences—definitely a
more complicated approach than Dedekind’s, but one more suited to modern analysis,
where convergent sequences (of objects which are not necessarily numbers) are the stock
in trade. All these definitions are equivalent, as it happens, so it does not matter which
one is used to define the line.
The important question is whether it is necessary to accept completed infinities to
arithmetize the concept of line. With hindsight, one can see how the cut defining √2,
say, might be explained away as a potential infinity (see the next section). But can the
infinity of real numbers be regarded as merely potential? This was one of the profound
questions answered by Cantor in the next episode of our story—the development of set
theory.
SETS
Cantor, like Dedekind, was drawn into accepting actual infinities in order to clarify the
meaning of points on the line. In Cantor’s case the problem was more technical (though
with a pedigree going back to the Pythagorean investigation of vibrating strings),
concerning the points of discontinuity of infinite sums of sine waves [9.9]. He found that
such a set of points could be very complicated. So complicated, in fact, that an operation
he used to ‘thin’ the set could be repeated infinitely often without removing all of it. He
therefore decided to apply his thinning operation ‘more than an infinite number of times’,
or rather, to continue applying it after the first infinity of applications was complete. The
implication was, of course, that this infinity of operations was actual.
To count the number of applications of the thinning operation, Cantor [9.11]
introduced ordinal numbers, a generalization of natural numbers to infinity and beyond.
The first infinite ordinal number, following the complete series 0, 1, 2, 3,…, is called ω.
It is followed by ω+1, ω+2, ω+3,…, and this second infinity of ordinal numbers
is followed by a number called ω'2. Any ordinal number α, like a natural number, has a
successor α+1. Cantor [9.11] called this the ‘first principle of generation’ of ordinal
numbers. He also introduced a second principle, which generates, ω, ω'2 and further
ordinals by wholesale actualization of infinities:
If any definite succession of defined whole real [i.e. ordinal] numbers exists, for
which there is no largest, then a new number is created, by means of this second
principle of generation, which is thought of as the limit of these numbers, i.e. it
is defined as the next number larger than all of them.
([9.11], 196)
In calling his ordinal numbers whole real numbers Cantor wished to stress their reality,
i.e. the reality of infinite sets, rather than any analogy with the real numbers (which is
reell in German and not the word real used by Cantor). There is a much better analogy
with the natural numbers, of course, though it is striking that the ordinals share the least
upper bound property with the real numbers. The relationship between the ordinals and
the real numbers was in fact an unsolved problem of Cantor’s set theory, the continuum
problem, and it remains today one of the great mysteries of mathematics. As will become
clearer below, the real numbers are generated by a principle which is possibly even more
powerful than Cantor’s second principle of generation for ordinal numbers.
Cantor’s investigation of sets of real numbers led him to another generalization of the
concept of natural number, the concept of cardinal number. Two sets A and B are said to
have the same cardinal number if there is a one-to-one correspondence or pairing
between the members of A and the members of B. The cardinal number of a finite set A is
simply the (natural) number of members of A, because if A has, say, seventeen members
then any set B whose members can be paired with the members of A will also have
seventeen members. The set of all natural numbers has an infinite cardinal number which
Cantor called ℵ₀
Cantor found that many seemingly ‘larger’ × sets can be put in one-to-one
correspondence with the natural numbers, and hence also have cardinal number ℵ₀. One
such set is the rational numbers. Another, as Cantor [9.10], found, is the algebraic
numbers. A number is called algebraic if it is the solution of an equation 
where a0, a1,…, an are integers. Cantor observed that if each such equation is assigned
the ‘height’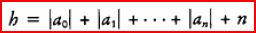 
then there are only finitely many equations with height h less than a given natural number
i. It is therefore possible to make a (potentially infinite) list consisting of all equations of
height ≤ 1, then all equations of height ≤ 2, then all equations of height ≤ 3…, thus
obtaining a list of all equations (*), in which each equation has some natural number
position j. This puts the equations (*) in one-to-one correspondence with the natural
numbers j. Finally, if each equation is replaced by the (finite) list of its solutions we get a
list of all algebraic numbers, on which each algebraic number appears at some natural
number position k.
The listing of the algebraic numbers is a very strong result, since it includes listings of
many other sets, in particular the integers and the rational numbers. It follows that all
these sets have cardinal number ℵ₀. However, it does not follow that the set of all real
numbers has cardinal number ℵ₀. It was already known, from the work of Liouville
[9.33], that certain real numbers are not algebraic. Cantor [9.10] discovered the more
dramatic result that almost all real numbers are not algebraic. He showed that the cardinal
number of the reals is not ℵ₀, by showing that the reals cannot be paired with the natural
numbers. This result is known as the non-denumerability or uncountability of the set of
real numbers.
Non-denumerability was so unprecedented that Cantor initially attempted to downplay
it as far as possible, calling his paper ‘On a Property of the Collection of All Real
Algebraic Numbers’ and using non-denumerability only to give a new proof of
Liouville’s result. (The algebraic numbers have cardinal number ℵ₀, the reals do not, so
not all reals are algebraic, QED.) He soon realized, however, that non-denumerability
was the gateway to a new world. It revealed the existence of cardinal numbers beyond
ℵ₀, so mathematics was able to distinguish different kinds of infinity. It also showed that
the real numbers could not be explained away as a potential infinity. For what is a
potential infinity but one whose members can be paired with the natural numbers?
As pointed out in the Introduction above, the natural numbers 0, 1, 2,…are the epitome
of a potential infinity—a list which includes any given member, if carried sufficiently far.
The non-denumerability of the reals means that any proposed listing of real numbers is
doomed to incompleteness—certain numbers (depending on the list, of course) will never
appear on it, no matter how long the list is continued.
In 1891 [9.12] Cantor gave a second proof of non-denumerability which makes the
futility of listing real numbers crystal clear. Suppose that x1, x2, x3,… is a list of real
numbers, and let xi be expanded as a decimal up to and including the ith decimal place.
For example, the list may begin like this: x1=17.7..., x2=0.16..., x3=2.131..., x4=0.7474..., x5=11.11312
… No matter how the list continues, a number x not
on it may be constructed by making x different from x1 in the first decimal place,
different from x2 in the second decimal place, different from x3 in the third decimal
place…, and so on. An explicit way to do this (which avoids getting an expansion which
is ultimately all 9s or all 0s, and hence expressible in two ways) is to let the ith decimal
place of x be 1 if the ith decimal place of x1, is not 1, and otherwise let it be 2. Thus no list
includes all the real numbers.
Since the number x is constructed from the sequence of digits along the diagonal of the
list, this technique came to be known as the diagonal argument. It was actually used
before Cantor by du Bois Reymond [9.16], though in a less transparent way. Cantor
[9.12] was the first to see that the diagonal argument was not simply a trick with numbers
but actually a fundamental insight into the relationship between sets and their subsets,
showing that any set has more subsets than members. This yields the astonishing
conclusion that there is no largest set.
To apply the diagonal argument in the general case let S be any set, and let Sx be a
sub-set paired with element x. (You may like to think of Sx laid out in a ‘row’ beside
element x, which is in a ‘column’ of the members of S.) Then one sub-set of S which is
not among the sets Sx is the ‘diagonal sub-set’ D defined as follows:
x belongs to D if and only if x does not belong to Sx.
This ensures that D is different from each Sx, with respect to the element x in fact, and
hence there are more sub-sets of S than members of S. The operation of forming all subsets
of a given set is called the power set operation. This is the operation, mentioned
above, which is possibly more powerful than the second principle of generation of ordinal
numbers. While the generation of ordinal numbers admits a larger number only when
there is some way of ‘approaching’ it, the power set operation creates a new set without
offering any means of approach.
In the case where S is the set of natural numbers it is easy to show (though a little
technical) that the power set of S has the same cardinal number as the set of real numbers.
Thus the continuum problem, which asks how big an ordinal number is required to count
the real numbers, is about the size of the power set of the natural members.
WHAT IS A NATURAL NUMBER?
With the help of the set concept, Dedekind had reduced the concept of real number to the
concept of rational number, as explained on pp. 255–7. Since relations between rational
numbers are equivalent to relations between natural numbers, this meant that all the
concepts of geometry and analysis were definable in terms of sets and the natural
numbers 0, 1, 2, 3,… Most mathematicians felt that this was as solid a foundation as it
was necessary or possible to have. After all, statements about the natural numbers were
not contested (the way the parallel axiom, or the intermediate value theorem had been, for
example) and no simpler concept than natural number seemed likely as a basis for
mathematics.
In taking this view, mathematicians tended to overlook the fact that the foundation was
not just the natural numbers, but natural numbers and sets. Sets were unavoidable, as
experience with the real numbers made clear, so if there was a simpler basis for
mathematics than natural numbers and sets it had to be just sets.
The first to grasp this possibility was Gottlob Frege, who developed a definition of
natural numbers in terms of sets, or more precisely in terms of properties, in his 1884
book Die Grundlagen der Arithmetik [9.19]. There is a subtle but important difference
between sets and properties (or concepts, as Frege called them). Corresponding to each
set S there is the property of belonging to S, and for each property P there is the extension
of P, consisting of all things with property P (or of all things which fall under concept P,
as Frege put it). However, the extension of a property can have paradoxical behaviour if
one assumes it to be a set (see pp. 266–8). This was not known in 1884, so there is no
distinction between sets and extensions of properties in the Grundlagen. To make a
distinction possible, and at the same time to give a concise description of Frege’s original
idea, we shall use the term class for the extension of a property.
Frege began with a highly entertaining demolition of previous attempts to define the
notion of number, then opened his own investigation by defining what it means for two
classes to have the same number. Like Cantor, he said that this is the case when there is a
one-to-one correspondence between their members, though he pointed out that for finite
classes this criterion had already been given by Hume (A Treatise of Human Nature,
Book I, part III, section I). Note that it is not necessary to use the number 1 to define one-to-
one correspondence. A relation ϕ(x,y) between the elements x of a class X and the
elements y of a class Y is a one-to-one correspondence if
for each x in X there is a y in Y such that ϕ(x,y),
for each y in Y there is an x in X such that ϕ(x,y),
if x≠x' and ϕ(x,y) and ϕ(x',y') then y≠y',
if y≠y' and ϕ(x,y) and ϕ(x',y') then x≠x'
The number of a class X may then be defined as the property of admitting a one-to-one
correspondence with X, i.e. the class of all classes that admit a one-to-one correspondence
with X ([9.19], 79).
Frege spent some time discussing the numbers 0 and 1. Any contradictory property
serves to define a class with number 0, and Frege used the property ‘not identical with
itself’. Thus 0 is the class of classes admitting a one-to-one correspondence with the
(empty) class of things not identical with themselves. The concept of the empty class was
novel, and Frege felt he would have to overcome some resistance to the idea:
Some may find it shocking that I should speak of a concept in this connection.
They will object, very likely, that it contains a contradiction and is reminiscent
of our old friends the square circle and the wooden iron. Now I believe that
these old friends are not so black as they are painted. To be of any use is, I
admit, the last thing we should expect of them; but at the same time, they cannot
do any harm, if only we do not assume that there is anything that falls under
them.
([9.19], 87).
Frege proceeded to show that the empty class is not only harmless, but wonderfully
fertile, by pulling the natural numbers out of it, one by one. First
1 is the number which belongs to the concept ‘identical with 0’.
([9.19], 90)
That is, 1 is the class of classes which admit one-to-one correspondence with the class
whose member is 0. Then to define n+1,
we shall choose the concept ‘number of the series of natural numbers ending
with n’.
([9.19], 92)
That is, n+1 is the class of classes which admit one-to-one correspondence with the class
whose members are 0, 1,…, n. Admittedly, there is something to be proved before we
know that ‘the series of natural numbers ending with n’ is well defined. However, this
was a matter of pure logic, which Frege already understood. As we shall see in the next
section, he had laid the foundations of mathematical logic in 1879.
Thus Frege’s work in 1884 was essentially the last step in a reduction of mathematics
to pure logic, the previous steps being the definition of the real numbers in terms of
rationals and the arithmetization of geometry and analysis. This stunning achievement
went unnoticed at the time, even by Frege himself. Strange as it may seem, Frege rejected
the arithmetization of geometry, so he missed the opportunity to extend his ideas beyond
the field of number. When Hilbert’s Grundlagen der Geometrie [9.28] appeared in 1899,
Frege wrote him several long letters ([9.20], 34) protesting against Hilbert’s definitions of
‘point’ and ‘line’ and insisting on spatial intuition as the source of geometric axioms. He
seemed oblivious to all that had happened in geometry since Kant. The opportunity Frege
missed was taken up by Bertrand Russell (with due credit to Frege) only after the turn of
the century.
WHAT IS LOGIC?
Logic has been a part of mathematics since ancient times, but until the nineteenth century
it was the least understood part. In mathematics there was no ‘theory’ of logic the way
there was a theory of numbers, for example, no attempt to analyse the content of logic
and to describe it completely. It is true that Leibniz and others had dreamed of making
logic as exact and mechanical as calculation, but little progress resulted from these
speculations. The proper understanding of logic arose from the attempt to understand the
foundations of mathematics, and eventually encompassed it.
The first important, though small, step was taken by George Boole. In his
Mathematical Analysis of Logic (1847, [9.6]) and The Laws of Thought (1854, [9.7]) he
introduced a logic of classes which is now known as Boolean algebra. In a deliberate
imitation of algebraic notation, he used x, y, z,…to denote classes, and let xy, x+y and
x−y denote intersection, union and relative complement respectively. Since a thing
belongs to
xy if and only if it belongs to x and to y, to x+y if and only if it belongs to x or
to y, to x−y if and only if it belongs to x and not to y,
the algebra of Boole’s product, sum and difference reflects the logic of ‘and’, ‘or’ and
‘not’, or propositional logic as it is now called. This algebra is not exactly the same as
ordinary algebra—for example, x2= x for any class x—but it was near enough for Boole
to venture the opinion that
There is not only a close analogy between the operations of the mind in general
reasoning and its operations in the particular science of Algebra, but there is to a
considerable extent an exact agreement in the laws by which the two classes of
operations are conducted.
([9.7], 6)
He was correct in thinking that his algebra was similar to ordinary algebra in its
operations and laws, but quite mistaken in thinking that such an algebra could reflect
‘general reasoning’. If thought was really as simple as Boole’s algebra we should not be
able to grasp very much mathematics, not even the concept of number, as Frege realized
in 1879. By reflecting on this difficulty, Frege was able to discover a vastly more
powerful system of logic.
The difference between Boole and Frege was that Boole was looking for a mathematics
of logic, whereas Frege was looking for a logic of mathematics. Boole’s search was less
fruitful, because the mathematics of his time contained a reflection of only a small part of
logic—the logic of ‘and’, ‘or’ and ‘not’. We can now see that Frege made a better choice,
but still it is astounding that he was able to succeed so completely at his first attempt.
Frege’s logical system came to life fully grown in his Begriffsschrift (Concept Writing)
of 1879 [9.18]. Unlike the Grundlagen of 1884, the Begriffsschrift is not a masterpiece of
clear and persuasive writing; in particular, most of its logical content is expressed in a
strange, labyrinthine symbolism of Frege’s own invention. Frege believed that the
structure of deduction is best revealed by displaying it in a two-dimensional, treelike
form. He managed to overcome his printer’s objections to this typographical nightmare,
but apparently forgot that readers, too, prefer symbols to follow one another in a
sequence. Fortunately it is now possible to translate the Begriffsschrift into a widely
accepted notation, and I shall do so in what follows.
The first difference one sees between Frege and Boole is that Frege regards the laws of
logic not as algebraic identities but as theorems derivable from axioms by certain rules of
inference. In the part of Frege’s logic that coincides with Boole’s, namely prepositional
logic, the difference shows itself as follows. Instead of Boole’s ‘and’, ‘or’ and ‘not’,
Frege uses ‘if…then’ and ‘not’, which we shall denote by ➙ and \Logic and the philosophy of mathematics in the nineteenth century respectively. This
difference is not really important, since ‘and’, ‘or’, ‘not’ are expressible in terms of ‘if…
then’, ‘not’ and vice versa, but ‘if…then’ and ‘not’ more naturally reflect the processes of
deduction. In terms of ➙, \Logic and the philosophy of mathematics in the nineteenth century, Frege’s axioms are:
It is one of the expository defects of the Begriffsschrift that Frege does not announce his
axioms. He does say, at the beginning of his section II, that ‘a small number of laws’ (the
axioms) ‘contain all of them’ (the theorems), but the reader finds the axioms only by
searching through a long series of sample derivations. His rules of inference have to be
found the same way; they are
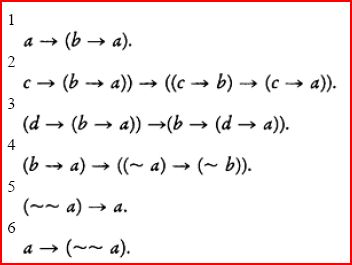Modus ponens: from theorems B and B B➙A A derive the theorem A (for
any formulae A, B). Substitution: from theorem A derive the result of
substituting, for each occurrence of a variable x in A, a formula ϕ(x).
Since it is very easy to confuse a rule of inference with a theorem of logic—for example,
modus ponens can be confused with the theorem b➙((b➙a)➙a) —Frege let
his readers down badly by not making these rules explicit in section II. It seems clear that
he did understand the difference between a theorem and a rule of inference. In his section
I he discusses the idea of a ‘mode of inference’ and mentions modus ponens in particular.
However, this was not clear enough for the logicians of his time, and they were still
confused thirty years later (see, for example, the indiscriminate mixture of axioms, rules
of inference and rules for the construction of formulae in Whitehead and Russell’s
Principia Mathematica, vol. I, part I, section A*1 [9.41]).
Frege offers no explanation for his claim that all laws of logic are consequences of his
axioms. In fact for prepositional logic this is not difficult to prove, though proofs did not
appear until around 1920. The claim is much more remarkable for his system as a whole,
which is a logic of properties and relations now known as predicate logic. (Here
‘predicate’ is used as a synonym for ‘relation’, and a property is a special case of a
relation.) The consideration of relations is the second, and major, difference between
Frege and Boole.
As we know from his analysis of the concept of number (pp. 261–3 above), Frege
recognized that reasoning about properties and relations was fundamental to mathematics.
He therefore decided to build the formulae of his logic from atomic formulae such as
P(x) ‘x has property P’
R(x, y) ‘x and y are in relation R’
etc. All mathematical statements can be built from such atomic formulae with the help of
the equality sign, =, the universal quantifiers, ∀ x (‘for all x’), ∀ y (‘for all y’), etc., and
the connectives , \Logic and the philosophy of mathematics in the nineteenth century of prepositional logic. The task then was to find all the laws of this
logic. Frege claimed that they could be obtained as theorems from the prepositional
axioms 1–6, plus the following rules and axioms specific to predicate logic.
➙ introduction rules: from theorem A(x) derive ∀; from theorem ∀xA(x)
derive B➙A(x) (when x does not occur in B). Axioms:
7B ➙ ∀xA(x), where f is any formula
8 c=c
9 (c=d) ➙ (f(c) ➙ f(d)), where c is any letter not in f.
Quite amazingly, he was right! However, this is a deep theorem, first proved by Gödel
[9.25], and it is doubtful that Frege fully understood the meaning of his claim, let alone
knew why it was true. It was enough that he had captured logic in a system, of axioms
and rules of inference—proving theorems about such a system was a task for a later
generation of logicians.
A FEW CLOUDS ON THE HORIZON
In the last decades of the nineteenth century, mathematicians enjoyed a period of
satisfaction with the foundations of their discipline, rather like that enjoyed by their
colleagues in physics (before the discovery of relativistic and quantum effects). Geometry
and analysis had been reduced to the theory of real numbers, the real numbers had been
reduced to sets of natural numbers, and nearly everybody was satisfied with the natural
numbers. If Frege’s work had been generally known the satisfaction could have been
even greater (despite Frege’s personal objection to the arithmetization of geometry),
because everything was wrapped up in his logic of classes. However, few were granted a
glimpse of this mathematical heaven, because Frege remained in obscurity until the turn
of the century. Then his logic became generally known only because Bertrand Russell
found something wrong with it.
The background to Russell’s discovery was this. In 1891 [9.12] Cantor introduced the
general diagonal argument which shows that any set S has more sub-sets than members,
as we saw on pp. 257–61 above. This obviously implies that there is no largest set, but it
has a more serious implication: there is no set of all sets. If there were, it would be the
largest set, by definition, yet the set of its sub-sets would be larger. Thus it is
contradictory to suppose that the class of all sets is itself a set. This was the first of the socalled
‘paradoxes’ of set theory. A similar paradox, involving the class of all ordinal
numbers, was published by Burali-Forti in 1897 [9.8]. Cantor did not discuss the
paradoxes in print, but he suggested a possible resolution of them in a letter to Dedekind
in 1899.
a multiplicity can be such that the assumption that all of its elements ‘are
together’ leads to a contradiction… If on the other hand the totality of elements
of a multiplicity can be thought of without contradiction as ‘being together’, so
that they can be gathered together into ‘one thing’, I call it a consistent
multiplicity or a ‘set’.
([9.13], 14).
In other words, to avoid contradictions, some classes should not be regarded as sets. This
in fact is the solution favoured today, but at the time it was not clear how to recognize the
inconsistent sets. Russell’s contribution was an analysis of the ‘set of all sets’ which
made its inconsistency more obvious.
Recall from pp. 257–61 how the diagonal construction is applied to a set S, with
members x and sub-sets Sx paired with the members. One constructs the diagonal sub-set
D of members x such that x does not belong to Sx. Then D differs from each Sx with
respect to x.
Now if S is the set of all sets x, then each subset y of S is also a member of S and we
can pair y (as a sub-set) with itself (as a member). The diagonal set D then consists of all
sets y such that y does not belong to y. Consequently, D differs from each set y with
respect to the member y: y belongs to D if and only if y does not belong to y. But D is
itself a member y of the set S of all sets, so D has the contradictory property of being
different from itself.
This is how Russell came to discover the inconsistency of the set D whose members
are the sets that do not belong to themselves. Of course, its inconsistency is obvious once
one has thought of it. Each of the two possibilities
(1) D belongs to D,
(2) D does not belong to D,
implies the other. However, it is not easy to see how to prevent logic from being infected
by such inconsistencies, and for this reason Russell’s discovery was a severe blow to
Frege (see Russell [9.39], Frege [9.21]). Most of the classes Frege used to define numbers
were inconsistent when regarded as sets, but if the logic of sets did not apply to them,
what did? Evidently logic would have to be overhauled, taking the properties of sets into
account, if inconsistencies were to be avoided.
Even if the paradoxical sets were successfully excluded, how could one be sure that
inconsistencies would not later arise in ‘indispensable’ parts of mathematics, such as
arithmetic and analysis? In view of the trouble arising from the diagonal construction,
one had to be suspicious of any field in which it was applicable, such as the theory of real
numbers.
Drastic cures for these ills were proposed by several mathematicians, especially those
who had not gone along with set theory in the first place. Kronecker refused to accept
completed infinities, and even denied the existence of irrational numbers. Poincaré and
Borel opposed the use of ‘self-referential’ definitions. However, Hilbert probably spoke
for the majority when he urged the construction of foundations to save as much as
possible of set-theoretic mathematics. In 1900 [9.29] he presented a list of twenty-three
problems to the mathematical community as tasks for the coming century. The first two
were concerned with foundations, and focused on the real numbers:
1 The continuum problem: decide whether each infinite set of real numbers
admits a one-to-one correspondence either with the set of natural numbers, or
with the set of all real numbers.
2 The consistency of arithmetic: prove that no contradiction can arise from
the axioms of arithmetic. (These axioms are essentially the basic properties of +,
× and < normally assumed for real numbers, together with the least upper bound
property.)
These two problems effectively exposed the two greatest difficulties in the nineteenthcentury
reduction of mathematics to logic. Firstly, the set concept was not clear. Between
the simplest infinite set (the set of natural numbers) and the set of all its sub-sets
(equivalently, the set of real numbers) was a gulf whose size and general nature was not
understood. Secondly, it was not clear that mathematical concepts were correctly
captured by axioms. The consequences of a given set of axioms were difficult to foresee
and they could conceivably include contradictions.
The answers to Hilbert’s problems 1 and 2 obtained so far do not boil down to a simple
yes or no. They reveal many aspects of the foundations of mathematics not anticipated in
the nineteenth century. The picture is no longer as simple as it once seemed, nevertheless
the general outline remains intact.
BIBLIOGRAPHY
9.1 Aubrey, J. Aubrey’s Brief Lives, Harmondsworth: Penguin, 1982.
9.2 Beltrami, E. ‘Risoluzione del problema: “Riportare i punti di una superficie sopra un
piano in modo che le linee geodetiche vengano rappresentate da linee rette”’, Opere
Matematiche, Milan, 1865:1 262–80.
9.3——‘Saggio di interpretazione della geometria non-euclidea’, Opere Matematiche,
Milan, 1868, 1:374–405.
9.4 Bolyai, J. Scientiam spatii absolute veram exhibens, Appendix to W.Bolyai,
Tentamen, Marosvásárhely 1832. English translation in R.Bonola, Noneuclidean
geometry, New York: Dover, 1955.
9.5 Bolzano, B. Rein analytischer Beweis des Lehrsatzes dass zwischen je zwey Werthen,
die ein entgegengesetzes Resultat gewähren, wenigstens eine reelle Wurzel der
Gleichung liege (1817), Ostwalds Klassiker, vol. 153, Leipzig: Engelmann, 1905.
9.6 Boole, G. The Mathematical Analysis of Logic, London and Cambridge, 1847.
9.7——An Investigation of the Laws of Thought, London, 1854.
9.8 Burali-Forti, C. ‘Una questione sui numeri tranfiniti’, Rendiconti del Circolo
matematico di Palermo, 11 (1897):154–64. English translation in From Frege to
Gödel, ed. J.van Heijenoort, Cambridge, Mass.: Harvard University Press, 1967:104–
11.
9.9 Cantor, G. ‘Über die Ausdehnung eines Satzes aus der Theorie der trigonometrischen
Reihen’, Mathematische Annalen, 5 (1872):123–32.
9.10——‘Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen’,
Journal für Mathematik 77 (1874):258–62.
9.11——Grundlagen einer allgemeinen Mannigfaltigkeitslehre, Leipzig, 1883.
9.12——Über eine elementare Frage der Mannigfaltigkeitslehre, Jahresbericht der
Deutsch. Math. Vereinigung 1 (1891):75–8.
9.13——Letter to Dedekind, 28 July 1899, in From Frege to Gödel, ed. J.van Heijenoort,
Cambridge, Mass.: Harvard University Press, 1967:113–17.
9.14 Dedekind, R. Stetigkeit und die Irrationalzahlen, Braunschweig, 1872, English
translation in Essays on the Theory of Numbers, Chicago: Open Court 1901.
9.15 Descartes, R. La Géométrie, Leyden, 1637, English translation, The Geometry, New
York: New York, 1954.
9.16 du Bois Reymond, P. ‘Über asymptotische Werthe, infinitäre Approximationen und
infinitäre Auflösungen von Gleichungen’, Mathematische Annalen, 7 (1874):363–7.
9.17 Fauvel, J. and Gray, J., eds, The History of Mathematics: a Reader, Basing-stoke,
Macmillan, 1987.
9.18 Frege, G. Begriffsschrift, Halle 1879. English translation in From Frege to Gödel,
Logic and the philosophy of mathematics in the nineteenth century 225
ed. J.van Heijenoort, Cambridge, Mass.: Harvard University Press, 1967:5–82.
9.19——Die Grundlagen der Arithmetik, Breslau, 1884. English translation, The
Foundations of Arithmetic, Oxford: Basil Blackwell 1953.
9.20——Letter to Hilbert, 27 December 1899, in Philosophical and Mathematical
Correspondence, Oxford: Basil Blackwell, 1980.
9.21——Letter to Russell, 22 June 1902, in From Frege to Gödel, ed. J.van Heijenoort,
Cambridge, Mass.: Harvard University Press, 1967:127–8.
9.22 Gauss, C.F. ‘Demonstratio nova theorematis omnem functionem algebraicum
rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi
posse’,Werke, Göttingen, 1799, 3:1–30.
9.23——Disquisitiones generales circa superficies curvas, Göttingen, 1827.
9.24——Letter to Schumacher, 28 November 1846, Briefwechsel mit H.C.Schumacher,
Hildesheim, Georg Olms Verlag, 1975 3:246–7.
9.25 Gödel, K. ‘Die Vollständigkeit der Axiome des logischen Funktionenkalküls’,
Monatshefte für Mathematik und Physik, 37 (1930):349–60. English translation in
From Frege to Gödel, ed. J.van Heijenoort, Cambridge, Mass.: Harvard University
Press, 1967:582–91.
9.26 Heath, T.L., ed., The Method of Archimedes, Cambridge: Cambridge University
Press, 1912.
9.27——The Thirteen Books of Euclid’s Elements, vol. 1, Cambridge, Cambridge
University Press, 1925.
9.28 Hilbert, D. Grundlagen der Geometrie, Leipzig: Teubner, 1899.
9.29——Mathematische Probleme, Göttinger Nachrichten, 1900:253–97.
9.30 Huygens, C. ‘Fourth part of a treatise on quadrature’, Oeuvres complètes, La Haye,
1659, 14:337.
9.31 Kant, I. Critique of Pure Reason, trans. N.K.Smith, London and Basingstoke,
Macmillan, 1929.
9.32 Kossak, E. Die Elemente der Arithmetik, Berlin: Programm Friedrichs-Werder.
Gymn., 1872.
9.33 Liouville, J. ‘Nouvelle démonstration d’un théorème sur les irrationelles
algébriques’, Comptes rendus de l’Acad. Sci. Paris, 18 (1844):910–11.
9.34 Lobachevsky, N.I. ‘Géométrie imaginaire,’ Journal für die reine und angewandte
Mathematik, 17 (1837):295–320.
9.35 Meray, C. ‘Remarques sur la nature des quantités définies par la condition de servir
de limites à des variables données,’ Revue des soc. savantes, sci. math. phys. nat., 4
(1869):280–9.
9.36 Minding, F. ‘Beiträge zur Theorie der kürzesten Linien auf krummen Flächen’,
Journal für die reine und angewandte Mathematik, 20(1840):323–7.
9.37 Newton, I. ‘Enumeratio linearum tertii ordinis’, Mathematical Papers, Cambridge,
1695, 7:588–645.
9.38 Riemann, G.F.B. ‘Über die Hypothesen, welche der Geometric zu Grunde liegen’,
Werke, Leipzig, 1854, 2nd edn: 272–87.
9.39 Russell, B. Letter to Frege, 16 June 1902, in From Frege to Gödel, ed. J.van
Heijenoort, Cambridge, Mass.: Harvard University Press, 1967:124–5.
9.40 Weierstrass, K. Einleitung in die Theorie der analytischen Funktionen, Göttingen:
Mathematische Institut der Universität Göttingen, 1874.
9.41 Whitehead, A.N. and B.Russell, Principia Mathematica, vol. 1, Cambridge:
Cambridge University Press, 1910.Routledge History of Philosophy. Taylor & Francis e-Library. 2005.