Akademik

комплексное многообразие, на к-ром можно ввести Кэлера метрику. Иногда такие многообразия на. з. многообразиями кэлерова типа, а термин "К. м." оставляется для многообразий, снабженных кэлеровой метрикой [1]. Всякое подмногообразие К. м. является К. м. В частности, все проективные комплексные алгебраич. многообразия без особых точек являются К. м., причем кэлерова метрика на них индуцируется Фубини - Штуди метрикой на комплексном проективном пространстве. Аналогично, всякое подмногообразие в аффинном пространстве (в частности, всякое Штейна многообразие).является кэлеровым. Другие примеры К. м. получаются, если рассматривать факторпространство М/Г К. м. Мпо дискретной группе аналитич. автоморфизмов Г, сохраняющих кэлерову метрику. В частности, любой комплексный тор есть К. м. Всякое одномерное комплексное многообразие кэлерово.

Теория гармония, форм на компактном К. м. дает следующие свойства групп когомологий де Рама и Дольбо на таком многообразии М(см. [1], [2], а также [5], где эти свойства были впервые доказаны для проективных алгебраич. многообразий):

Голоморфные формы на компактном К. м. замкнуты. В частности,

где А ¹- пространство всех голоморфных 1-форм на М. В случае число есть род компактной римановой поверхности М. На указанных выше свойствах основано построение примеров некэлеровых компактных многообразий, простейшим из к-рых является поверхность Хопфа, диффеомор-фная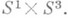

К. м. Мназ. многообразием Ходжа, если кэлерова метрика на Мявляется метрикой Ходжа. Всякое проективное алгебраич. многообразие без особых точек является многообразием Ходжа относительно метрики, индуцированной метрикой Фубини - Штуди. Обратно, всякое компактное комплексное многообразие М, снабженное кзлеровой метрикой Ходжа h, допускает биголоморфное вложение в комплексное проективное пространство, причем метрика на М, индуцированная метрикой Фубини - Штуди, имеет вид kh, где k - натуральное число [1], [3] (теорема Кодаиры о проективном вложении). Таким образом, компактное комплексное многообразие Мизоморфно проективному алгебраич. многообразию тогда и только тогда, когда М - многообразие Ходжа Другая форма этого критерия состоит в том что компактное комплексное многообразие Мявляется проективным алгебраич. многообразием тогда и только тогда, когда на Мсуществует отрицательное расслоение на комплексные прямые. Теорема Кодаиры допускает сообщение на комплексные пространства (см. [4], [6]). Компактные К. м., не являющиеся многообразиями Ходжа, можно найти среди двумерных комплексных торов. Напр., этим свойством обладает тор где Г - решетка, натянутая на векторы (1,0), (0,1), (см. [1], [3]). Другое необходимое и достаточное условие проективности re-мерного компактного кэлерова многообразия Мсостоит в наличии на М п алгебраически независимых мероморфных функций.

Всякое некомпактное полное К. м., имеющее положительную секционную кривизну, является многообразием Штейна. Тем же свойством обладает любое одно-связное полное К. м. неположительной секционной кривизны [7].

Лит.:[1] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [2] В е й л ь А., Введение в теорию кэлеровых многообразий, пер. с франц., М., 1961; [3] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [4] Ганнинг Р., Росси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969; [5] Hodge W. V. D., The theory and applications of harmonic integrals, 2 ed., Camb., 1952; 16] Грауэрт Г., в кн.: Комплексные пространства. Сб. пер., М., 1965, с. 45-104; [7] G r е е n е R. Е., W u H., в сб.: Value-Distribution Theory. Part A, N. Y., 1974, p. 145-67. А. Л. Онищик.