Akademik

расстояние на множестве X,- определенная на декартовом произведении функция р с неотрицательными действительными значениями, удовлетворяющая при. любых условиям:

1)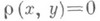тогда и только тогда, когда (аксиома тождества);

2)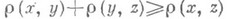 (аксиома треугольника);

3) (аксиома симметрии).

Множество X, на к-ром может быть введена М., наз. метризуемым. Множество X, наделенное некоторой М., наз. метрическим пространством.

Примеры. 1) На любом множестве имеется дискретная метрика:

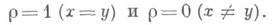
2) В пространстве возможны разные М., среди них:

здесь

3) В римановом пространстве М. определяется метрическим тензором или дифференциальной квадратичной формой (в нек-ром смысле это - аналог первой М. из примера 2)). Обобщение М. этого типа см. в ст. Финслерово пространство.

4) В функциональных пространствах над (би)компактом X также вводятся разные М., напр, равномерная метрика

(аналог второй М., из примера 2)), интегральная метрика

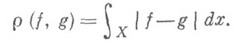
5) В нормированном пространстве над 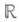М. определяется через норму :

В нормированном кольце - более сложная формула:

6) В метрич. пространстве вводится другая М.- т. н. внутренняя метрика.

7) В пространстве замкнутых подмножеств метрич. пространства определяется хаусдорфова метрика.

Следует заметить, что в традиционном определении М. условие 3) и требование неотрицательности излишни, т. е. вытекают уже из достаточности условия 1) и условия 2).

Если вместо 1) выполняется лишь условие: , если (так что при не всегда ), функция 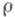наз. псевдометрикой [2], [3], или отклонением [4].

М. (и даже псевдометрика) позволяет определить ряд дополнительных структур на множестве X.

Прежде всего, это - топология (см. Топологическое пространство), кроме того - равномерная (см. Равномерное пространство )или близостная (см. Близости пространство )структуры. Термин М. используется также и для обозначения более общих понятий, к-рые не обладают всеми свойствами 1) - 3), таковы, напр., индефинитная метрика, симметрика и т. д.

Лит.:[1] Александров П. С, Введение в теорию множеств и общую топологию, М., 1977; [2] Келли Д ж.-Л., Общая топология, пер. с англ., М., 1968; [3] Куратовский К., Топология, [пер. с англ.], т. 1, М., 1966; [4] Бурбаки Н., Общая топология. Использование вещественных чисел в общей топологии. Функциональные пространства. Сводка результатов. Словарь, пер. с франц., М., 1975.

М. И. Войцеховский.