-1) О. т. аналитической функции f(z) - препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого-либо пути на плоскости этого переменного.
Пусть аналитическая функция f(z) определена некоторым вейерштрассовым элементом (U(z, R), fz), состоящим из степенного ряда

и его круга 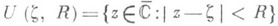 сходимости
сходимости
с центром 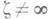 и радиусом сходимости R>0. Рассмотрим всевозможные пути
и радиусом сходимости R>0. Рассмотрим всевозможные пути 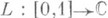 , т. е. непрерывные отображения
, т. е. непрерывные отображения 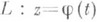 отрезка
отрезка  в расширенную комплексную плоскость
в расширенную комплексную плоскость 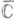 , начинающиеся в центре этого элемента
, начинающиеся в центре этого элемента  . Если аналитич. родолжение данного элемента возможно вдоль любого такого пути в любую точку
. Если аналитич. родолжение данного элемента возможно вдоль любого такого пути в любую точку  , то получающаяся при этом полная аналитич. ция f(z) сводится к константе: f(z)=const. Для нетривиальных же аналитич. ций f(z)
, то получающаяся при этом полная аналитич. ция f(z) сводится к константе: f(z)=const. Для нетривиальных же аналитич. ций f(z)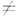 const характерно существование препятствии для аналитич. родолжения вдоль нек-рых путей L.
const характерно существование препятствии для аналитич. родолжения вдоль нек-рых путей L.
Пусть точка арасширенной плоскости С расположена на пути 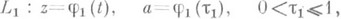
 , и на пути
, и на пути 
 , причем аналитич. родолжение вдоль L1 и L2 осуществимо во все предшествующие точки z=j1(t),
, причем аналитич. родолжение вдоль L1 и L2 осуществимо во все предшествующие точки z=j1(t),  , и
, и 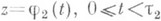 . Два таких пути L1 и L2 наз. эквивалентными по отношению аналитич. родолжению данного элемента (U(z, R), fz). в точку а, если для любой окрестности V(а).точки ав С существует такое число
. Два таких пути L1 и L2 наз. эквивалентными по отношению аналитич. родолжению данного элемента (U(z, R), fz). в точку а, если для любой окрестности V(а).точки ав С существует такое число  , что вейерштрассов элемент, получаемый из (U(z, R), fz) посредством аналитич. родолжения вдоль L1 до какой-либо точки
, что вейерштрассов элемент, получаемый из (U(z, R), fz) посредством аналитич. родолжения вдоль L1 до какой-либо точки 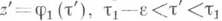 , может быть продолжен вдоль нек-рого пути, расположенного в V(a), в элемент, получаемый посредством продолжения вдоль L2 из (U(z, R), fz). до какой-либо точки z"=j2(t"), t2-e<t"<t2.
, может быть продолжен вдоль нек-рого пути, расположенного в V(a), в элемент, получаемый посредством продолжения вдоль L2 из (U(z, R), fz). до какой-либо точки z"=j2(t"), t2-e<t"<t2.
Если аналитич. родолжение в точку аосуществимо вдоль нек-рого пути L, то оно возможно и вдоль всех путей класса эквивалентности {L}, содержащего L. В этом случае пара (a, {L}).наз. регулярной, или правильной; она определяет однозначную регулярную ветвь аналитич. ции f(z) в окрестности точки V(а).
Если же аналитич. родолжение вдоль нек-рого пути 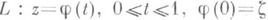 , проходящего через
, проходящего через  , осуществимо во все точки
, осуществимо во все точки  ,
, 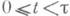 , предшествующие а, но не осуществимо в точку
, предшествующие а, но не осуществимо в точку 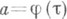 , то аесть особая точка при аналитическом продолжении элемента (U(z, R), fz) вдоль пути L. В этом случае она будет особой и при продолжении вдоль всех проходящих через апутей класса эквивалентности {L}. Пара (a, {L}), состоящая из точки
, то аесть особая точка при аналитическом продолжении элемента (U(z, R), fz) вдоль пути L. В этом случае она будет особой и при продолжении вдоль всех проходящих через апутей класса эквивалентности {L}. Пара (a, {L}), состоящая из точки  и класса эквивалентности {L} путей L, проходящих через а, для каждого из к-рых точка аособая, наз. особой точкой аналитической функции f(z), определяемой элементом (U(z, R), fz). Две О. т. (a, {L}).и (b, {M}).считаются совпадающими, если а=b и совпадают классы{L} и {М}. При этом точка арасширенной комплексной плоскости
и класса эквивалентности {L} путей L, проходящих через а, для каждого из к-рых точка аособая, наз. особой точкой аналитической функции f(z), определяемой элементом (U(z, R), fz). Две О. т. (a, {L}).и (b, {M}).считаются совпадающими, если а=b и совпадают классы{L} и {М}. При этом точка арасширенной комплексной плоскости  наз. проекцией, или z-коордииатой, О. т. (a, {L});говорят также, что О. т. (a, {L}).расположена над точкой
наз. проекцией, или z-коордииатой, О. т. (a, {L});говорят также, что О. т. (a, {L}).расположена над точкой  . В общем случае над одной и той же точкой
. В общем случае над одной и той же точкой  могут располагаться несколько и даже счетное множество различных особых и регулярных пар (a, {L}), получающихся при аналитич. родолжении одного и того же элемента (U(z, R), fz).
могут располагаться несколько и даже счетное множество различных особых и регулярных пар (a, {L}), получающихся при аналитич. родолжении одного и того же элемента (U(z, R), fz).
Если радиус сходимости исходного ряда (1)  , то на окружности
, то на окружности 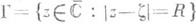 круга сходимости U(z, R).непременно имеется хотя бы одна особая точка аэлемента (U(z, R), fz), то есть О. т. аналитич. ции f(z) при продолжении вдоль путей
круга сходимости U(z, R).непременно имеется хотя бы одна особая точка аэлемента (U(z, R), fz), то есть О. т. аналитич. ции f(z) при продолжении вдоль путей  , класса {L} таких, что
, класса {L} таких, что  при
при 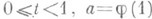 . Иначе говоря, О. т. элемента (U(z, R), fz) - это такая точка
. Иначе говоря, О. т. элемента (U(z, R), fz) - это такая точка  , что непосредственное аналитич. родолжение элемента (U(z, R), fz) из круга U(z, R).в любую окрестность V(а).невозможно. В этой ситуации и вообще во всех случаях, когда отсутствие явного описания класса путей {L} не может повести к недоразумениям, ограничиваются обычно только указанием z-координаты О. т. а. Изучение расположения О. т. аналитич. ции в зависимости от свойств последовательности коэффициентов
, что непосредственное аналитич. родолжение элемента (U(z, R), fz) из круга U(z, R).в любую окрестность V(а).невозможно. В этой ситуации и вообще во всех случаях, когда отсутствие явного описания класса путей {L} не может повести к недоразумениям, ограничиваются обычно только указанием z-координаты О. т. а. Изучение расположения О. т. аналитич. ции в зависимости от свойств последовательности коэффициентов 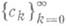 исходного элемента (U(z, R), fz) является одним из важных направлений исследований в теории функций (см. Адамара теорема мультипликационная, Звезда, элемента функции, а также [1], [3], [5]). Известно, напр., что О. т. ряда
исходного элемента (U(z, R), fz) является одним из важных направлений исследований в теории функций (см. Адамара теорема мультипликационная, Звезда, элемента функции, а также [1], [3], [5]). Известно, напр., что О. т. ряда

где  - натуральное число, заполняют всю границу
- натуральное число, заполняют всю границу 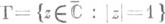 его круга сходимости U(0,1), хотя сумма этого ряда непрерывна всюду в замкнутом круге
его круга сходимости U(0,1), хотя сумма этого ряда непрерывна всюду в замкнутом круге 
Здесь окружность Г есть естественная граница аналитич. ции f0(z), аналитич. родолжение f0(z) за пределы круга U(0, 1). невозможно. Пусть в достаточно малой окрестности 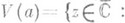
 точки
точки 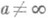 (или
(или  ) аналитич. родолжение элементов, получаемых вдоль путей определенного класса {L}, возможно во все точки, отличные от а, т. е. по всем путям, расположенным в проколотой окрестности V'(a) = =
) аналитич. родолжение элементов, получаемых вдоль путей определенного класса {L}, возможно во все точки, отличные от а, т. е. по всем путям, расположенным в проколотой окрестности V'(a) = =  (соответственно V'(
(соответственно V'(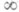 )=
)= ); тогда О. т. (a, {L}).наз. изолированной особой точкой. Если при этом аналитич. родолжение элементов, получаемых вдоль путей класса {L}, по всевозможным замкнутым путям, расположенным в V(а), не изменяет этих элементов, то изолированная О. т. (a, {L}).наз. особой точкой однозначного характера. Такая О. т. может быть полюсом или существенно особой точкой: если существует бесконечный предел lim f(z)=
); тогда О. т. (a, {L}).наз. изолированной особой точкой. Если при этом аналитич. родолжение элементов, получаемых вдоль путей класса {L}, по всевозможным замкнутым путям, расположенным в V(а), не изменяет этих элементов, то изолированная О. т. (a, {L}).наз. особой точкой однозначного характера. Такая О. т. может быть полюсом или существенно особой точкой: если существует бесконечный предел lim f(z)= при стремлении
при стремлении  вдоль путей класса {L}, то О. т. однозначного характера (a, {L}) наз. полюсом;если не, существует никакого конечного или бесконечного предела lim f(z) при стремлении z->a вдоль путей класса {L}, то (a, {L})-существенно особая точка;случай конечного предела соответствует регулярной паре (a, {L}). Если же аналитич. родолжение элементов, получаемых вдоль путей класса {L}, по замкнутым путям, окружающим в V' (а).точку а, изменяет эти элементы, то изолированная О. т. (a, {L}).наз. ветвления точкой, или особой точкой многозначного характера. Класс точек ветвления, в свою очередь, подразделяется на алгебраические точки ветвления и трансцендентные точки ветвления (включая логарифмические точки ветвления). Если после нек-рого конечного числа
вдоль путей класса {L}, то О. т. однозначного характера (a, {L}) наз. полюсом;если не, существует никакого конечного или бесконечного предела lim f(z) при стремлении z->a вдоль путей класса {L}, то (a, {L})-существенно особая точка;случай конечного предела соответствует регулярной паре (a, {L}). Если же аналитич. родолжение элементов, получаемых вдоль путей класса {L}, по замкнутым путям, окружающим в V' (а).точку а, изменяет эти элементы, то изолированная О. т. (a, {L}).наз. ветвления точкой, или особой точкой многозначного характера. Класс точек ветвления, в свою очередь, подразделяется на алгебраические точки ветвления и трансцендентные точки ветвления (включая логарифмические точки ветвления). Если после нек-рого конечного числа  однократных обходов точки ав одном и том же направлении в V' (а). элементы, получаемые вдоль путей класса {L}, принимают исходный вид, то ({a, {L}).есть алгебраич. точка ветвления и число т-1 наз. ее порядком. В противном случае, когда обходы точки a дают все новые и новые элементы, (a, {L}).есть трансцендентная точка ветвления.
однократных обходов точки ав одном и том же направлении в V' (а). элементы, получаемые вдоль путей класса {L}, принимают исходный вид, то ({a, {L}).есть алгебраич. точка ветвления и число т-1 наз. ее порядком. В противном случае, когда обходы точки a дают все новые и новые элементы, (a, {L}).есть трансцендентная точка ветвления.
Напр., для функции

точки 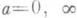 (для всех путей) являются алгебраич. точками ветвления порядка 5. Как однозначную функцию точки f(z) можно представить только на соответствующей римановой поверхности S, состоящей из 6 листов над
(для всех путей) являются алгебраич. точками ветвления порядка 5. Как однозначную функцию точки f(z) можно представить только на соответствующей римановой поверхности S, состоящей из 6 листов над 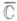 , определенным образом соединенных над точками
, определенным образом соединенных над точками 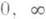 . Кроме того, над точкой а=1 расположены три правильные ветви f(z), однозначные на трех соответствующих листах S;на одном листе Sрасположен полюс второго порядка и на двух листах S - полюсы первого порядка. Вообще, привлечении понятия римановой поверхности оказывается весьма удобным и плодотворным при изучении характера О. т.
. Кроме того, над точкой а=1 расположены три правильные ветви f(z), однозначные на трех соответствующих листах S;на одном листе Sрасположен полюс второго порядка и на двух листах S - полюсы первого порядка. Вообще, привлечении понятия римановой поверхности оказывается весьма удобным и плодотворным при изучении характера О. т.
Если радиус сходимости исходного ряда (1)  , то он представляет целую функцию f(z), голоморфную во'всей конечной плоскости С. Такая функция в случае
, то он представляет целую функцию f(z), голоморфную во'всей конечной плоскости С. Такая функция в случае  имеет единственную изолированную О. т.
имеет единственную изолированную О. т.  однозначного характера; если при этом
однозначного характера; если при этом
 - полюс, то f(z) есть целая рациональная функция, или многочлен; если же
- полюс, то f(z) есть целая рациональная функция, или многочлен; если же
 - существенно особая точка, то f(z) есть целая трансцендентная функция.
- существенно особая точка, то f(z) есть целая трансцендентная функция.
Мероморфная функция f(z) в конечной плоскости С получается, когда аналитич. родолжение ряда (1) приводит к однозначной аналитич. ции f(z) в С, имеющей в С в качестве О. т. только полюсы. Если при этом и 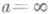 есть полюс или регулярная точка, то общее число всех полюсов f(z) в расширенной плоскости
есть полюс или регулярная точка, то общее число всех полюсов f(z) в расширенной плоскости 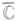 конечно и f(z) есть рациональная функция. Для трансцендентной мероморфной функции f(z) в
конечно и f(z) есть рациональная функция. Для трансцендентной мероморфной функции f(z) в 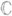 бесконечно удаленная точка
бесконечно удаленная точка  может оказаться предельной точкой полюсов - это простейший пример неизолированной О. т. однозначной аналитич. ции. Мероморфная функция в произвольной области
может оказаться предельной точкой полюсов - это простейший пример неизолированной О. т. однозначной аналитич. ции. Мероморфная функция в произвольной области  определяется аналогично.
определяется аналогично.
Вообще говоря, проекции неизолированных О. т. могут образовывать различные множества точек расширенной комплексной плоскости 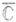 . В частности, какова бы ни была область
. В частности, какова бы ни была область  , существует аналитич. ция
, существует аналитич. ция 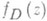 в D, для к-рой Dявляется ее естественной областью существования, а граница Г= дD - естественной границей, так что аналитич. родолжение функции fD(z) за пределы области Dневозможно. При этом естественная граница Г состоит из достижимых и недостижимых точек (см. Граничные элементы). Если точка
в D, для к-рой Dявляется ее естественной областью существования, а граница Г= дD - естественной границей, так что аналитич. родолжение функции fD(z) за пределы области Dневозможно. При этом естественная граница Г состоит из достижимых и недостижимых точек (см. Граничные элементы). Если точка  достижима вдоль путей класса {L} (таких классов может быть и несколько), расположенных целиком, кроме конечной точки а, в области D, то над ней необходимо расположены только О. т. функции, fD(z), т. к. в противном случае было бы возможно аналитич. родолжение fD(z) за пределы области Dчерез нек-рую часть Г в окрестности точки а; достижимые точки образуют плотное множество на Г.
достижима вдоль путей класса {L} (таких классов может быть и несколько), расположенных целиком, кроме конечной точки а, в области D, то над ней необходимо расположены только О. т. функции, fD(z), т. к. в противном случае было бы возможно аналитич. родолжение fD(z) за пределы области Dчерез нек-рую часть Г в окрестности точки а; достижимые точки образуют плотное множество на Г.
В качестве определяющего элемента аналитич. ции f(z) многих комплексных переменных z=(z1,...,zn), n>l, можно принять, напр., вейерштрассов элемент (Un(z, R), fz) в виде кратного степенного ряда

и поликруга сходимости этого ряда
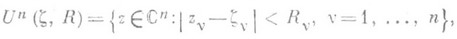
имеющего центр  и радиус сходимости R={R1>0, . . ., Rn>0}. Полагая в основу процесс аналитич. родолжения элемента (2) вдоль всевозможных путей
и радиус сходимости R={R1>0, . . ., Rn>0}. Полагая в основу процесс аналитич. родолжения элемента (2) вдоль всевозможных путей  , отображающих отрезок
, отображающих отрезок 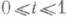 в комплексное пространство С n, получают общее определение О. т.
в комплексное пространство С n, получают общее определение О. т.  , функции f(z), формально вполне аналогичное приведенному выше для случая n=1.
, функции f(z), формально вполне аналогичное приведенному выше для случая n=1.
Однако вследствие переопределенности Ноши - Римана условий при n>1 и проистекающей отсюда "большей силы" аналитич. родолжения случай n>1 коренным образом отличается, по существу, от случая п=1. В частности, при n>1 существуют такие области  , к-рые не могут быть естественными областями существования никакой однозначной аналитической, или голоморфной, функции. Иначе говоря, определенные участки границы
, к-рые не могут быть естественными областями существования никакой однозначной аналитической, или голоморфной, функции. Иначе говоря, определенные участки границы  _ такой области свободны от О. т. любой голоморфной функции f(z), заданной в D, и через них возможно аналитич. родолжение. Напр., справедлива теорема Осгуда - Брауна: если компакт Красположен в ограниченной области
_ такой области свободны от О. т. любой голоморфной функции f(z), заданной в D, и через них возможно аналитич. родолжение. Напр., справедлива теорема Осгуда - Брауна: если компакт Красположен в ограниченной области 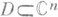 , причем
, причем  является также областью, и функция f(z) голоморфна в
является также областью, и функция f(z) голоморфна в  , то она голоморфно продолжается на всю область D(см. также Устранимое множество). Естественные области существования голоморфных функций наз. иначе голоморфности областями, они характеризуются определенными геометрич. свойствами. Аналитически продолжая голоморфную функцию f(z), заданную первоначально в области
, то она голоморфно продолжается на всю область D(см. также Устранимое множество). Естественные области существования голоморфных функций наз. иначе голоморфности областями, они характеризуются определенными геометрич. свойствами. Аналитически продолжая голоморфную функцию f(z), заданную первоначально в области  , и желая сохранить ее однозначность, приходят к необходимости введения, вообще говоря, многолистных над
, и желая сохранить ее однозначность, приходят к необходимости введения, вообще говоря, многолистных над  областей голоморфности на римановых областях- аналогах римановых поверхностей. В этой трактовке оказывается, что О. т. голоморфной функции f(z) - это точки границы
областей голоморфности на римановых областях- аналогах римановых поверхностей. В этой трактовке оказывается, что О. т. голоморфной функции f(z) - это точки границы 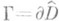 ее области голоморфности
ее области голоморфности 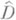 Теорема Осгуда - Брауна показывает, что связные компоненты Г не могут образовывать компактных множеств K таких, что в
Теорема Осгуда - Брауна показывает, что связные компоненты Г не могут образовывать компактных множеств K таких, что в 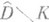 функция f(z) голоморфна. В частности, при n>1 не существует изолированных О. т. голоморфных функций.
функция f(z) голоморфна. В частности, при n>1 не существует изолированных О. т. голоморфных функций.
Простейшие типы О. т. аналитич. ций многих комплексных переменных доставляют мероморфные функции f(z) в области 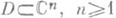 , характеризующиеся следующими свойствами: 1) f(z) голоморфна всюду в D, за исключением полярного множества Р, состоящего из О. т.; 2) для любой точки
, характеризующиеся следующими свойствами: 1) f(z) голоморфна всюду в D, за исключением полярного множества Р, состоящего из О. т.; 2) для любой точки 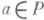 существуют окрестность V(a).и голоморфная в V(а) функция
существуют окрестность V(a).и голоморфная в V(а) функция  такие, что функция
такие, что функция  голоморфно продолжается в V(a). При этом О. т.
голоморфно продолжается в V(a). При этом О. т. 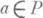 делятся на полюсы, в к-рых
делятся на полюсы, в к-рых  , и точки неопределенности, в к-рых
, и точки неопределенности, в к-рых  . В случае полюса
. В случае полюса  при стремлении
при стремлении  ; в любой окрестности точки неопределенности f(z) принимает все значения
; в любой окрестности точки неопределенности f(z) принимает все значения  . Напр., мероморфяая функция
. Напр., мероморфяая функция  в
в  имеет в качестве полярного множества прямую
имеет в качестве полярного множества прямую 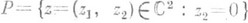 , все точки к-рой суть полюсы, за исключением одной точки неопределенности (0,0). Мероморфная функция f(z) в своей области голоморфности
, все точки к-рой суть полюсы, за исключением одной точки неопределенности (0,0). Мероморфная функция f(z) в своей области голоморфности  представима глобальна в
представима глобальна в 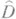 в виде отношения двух голоморфных функций, т. е. ее полярное множество Р. есть аналитическое множество.
в виде отношения двух голоморфных функций, т. е. ее полярное множество Р. есть аналитическое множество.
Точка  наз. точкой мероморфности функции f(z), если f(z) мероморфна в нек-рой ее окрестности; таким образом, если О. т. есть точка мероморфности, то она либо полюс, либо точка неопределенности. Все остальные О. т. аналитич. ции f(z), не являющиеся точками мероморфности, иногда наз. существенно особыми точками. К ним относятся, напр., точки ветвления f(z), т. о. точки ветвления ее (многолистной) области голоморфности
наз. точкой мероморфности функции f(z), если f(z) мероморфна в нек-рой ее окрестности; таким образом, если О. т. есть точка мероморфности, то она либо полюс, либо точка неопределенности. Все остальные О. т. аналитич. ции f(z), не являющиеся точками мероморфности, иногда наз. существенно особыми точками. К ним относятся, напр., точки ветвления f(z), т. о. точки ветвления ее (многолистной) области голоморфности  . Размерность множества всех О. т. голоморфной функции f(z) в общем случае равна 2n-1. При нек-рых дополнительных ограничениях на f(z) это множество оказывается аналитическим (и, следовательно, имеющим меньшую размерность; см. [2]).
. Размерность множества всех О. т. голоморфной функции f(z) в общем случае равна 2n-1. При нек-рых дополнительных ограничениях на f(z) это множество оказывается аналитическим (и, следовательно, имеющим меньшую размерность; см. [2]).
Лит.:[1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1-2, М., 1967-68; [2] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976; [3] Стоилов с., Теория функций комплексного переменного, пер. с рум., т. 1-2, М., 1962; [4] Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968; [5] Бибербах Л., Аналитическое продолжение, пер. с нем., М., 1967; [6] Bieberbach L., Lehrbuch der Funktionentheorie, 3 Aufl., Bd 1, Lpz.-В., 1930, Bd 2, Lpz.- В., 1927; [7] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [8] Ф у к с Б. А., Введение в теорию аналитических функций многих комплексных переменных, 2 изд., М., 1962; [9] Ганнинг Р.,Росси Х., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969; [10] Веhnkе Н., Thullen P., Theorie der Funktionen mehrerer komplexer Veranderlichen, В., 1934. Е. Д. Соломенцев.
2).О. т., особенность, алгебраического многообразия - точка, в к-рой нарушается гладкость. Точнее,, пусть X - алгебраич. многообразие или схема конечного типа над полем k, тогда точка  наз. особой, если соответствующее локальное кольцо
наз. особой, если соответствующее локальное кольцо 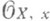 не регулярно (регулярность локального нётерова кольца Ас максимальным идеалом m означает равенство
не регулярно (регулярность локального нётерова кольца Ас максимальным идеалом m означает равенство  ). Множество О. т. алгебраич. многообразия Xзамкнуто в топологии Зариского и обозначается Sing X. Если X - приведенное многообразие, то Sing Xнигде не плотно в X. Если хявляется изолированной точкой в Sing X, то хназ. изолированной О. т. Для проверки того, будет ли точка
). Множество О. т. алгебраич. многообразия Xзамкнуто в топологии Зариского и обозначается Sing X. Если X - приведенное многообразие, то Sing Xнигде не плотно в X. Если хявляется изолированной точкой в Sing X, то хназ. изолированной О. т. Для проверки того, будет ли точка  особой или неособой, используется якобиев критерий (см. Гладкая схема).
особой или неособой, используется якобиев критерий (см. Гладкая схема).
Разрешением особенности (десингуляризацией) алгебраич. многообразия Xпаз. собственный бирациональный морфизм  , где
, где
 - гладкое многообразие. Существование разрешения особенностей доказано для широкого класса многообразий, в частности для всех многообразий над полем характеристики 0 (см. [13]); как правило, оно не единственно. Разрешение особенностей используется для введения различных инвариантов многообразия X;примером служат пространства когомологий
- гладкое многообразие. Существование разрешения особенностей доказано для широкого класса многообразий, в частности для всех многообразий над полем характеристики 0 (см. [13]); как правило, оно не единственно. Разрешение особенностей используется для введения различных инвариантов многообразия X;примером служат пространства когомологий  . Нормальное многообразие X, для к-рого
. Нормальное многообразие X, для к-рого  при всех i>0, наз. многообразием с рациональными особенностями. Рациональными являются тороидальные особенности [6] и особенности многообразий Шуберта [3]. Размерность пространства
при всех i>0, наз. многообразием с рациональными особенностями. Рациональными являются тороидальные особенности [6] и особенности многообразий Шуберта [3]. Размерность пространства 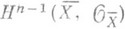 для п-мерного многообразия Xназ. геометрическим родом X. См. также Разрешение особенностей.
для п-мерного многообразия Xназ. геометрическим родом X. См. также Разрешение особенностей.
Теория деформаций особенностей, т. е. многообразий с О. т., строится параллельно теории деформаций (гладких) алгебраич. многообразий. Деформацией многообразия Х п наз. плоский морфизм 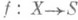 такой, что
такой, что  для нек-рой
для нек-рой  ; многообразие Sпри этом наз. базой деформации. Для многообразия Х 0 с изолированной О. т. существует версальная деформация, содержащая все деформации многообразия Х 0. Может оказаться, что особенность жесткая, т. е. база версальной деформации ее состоит из одной точки и все ее деформации тривиальны [4]. Противоположными к жестким являются сглаживаемые О. т., в базе Sверсальной деформации к-рых есть такие точки, что
; многообразие Sпри этом наз. базой деформации. Для многообразия Х 0 с изолированной О. т. существует версальная деформация, содержащая все деформации многообразия Х 0. Может оказаться, что особенность жесткая, т. е. база версальной деформации ее состоит из одной точки и все ее деформации тривиальны [4]. Противоположными к жестким являются сглаживаемые О. т., в базе Sверсальной деформации к-рых есть такие точки, что 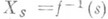 неособы. Множество Dточек
неособы. Множество Dточек  с особыми Xs наз. дискриминантным подмножеством.
с особыми Xs наз. дискриминантным подмножеством.
При изучении деформаций большую роль играет действие группы монодромии  на когомологиях слоев X.
на когомологиях слоев X.
Одновременным разрешением особенностей семейства  наз. собственный морфизм
наз. собственный морфизм  такой, что
такой, что 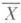 - гладкая S-схема и для любого
- гладкая S-схема и для любого  морфизм
морфизм  является разрешением особенностей. Нереальная деформация простых О. т. (см. ниже) допускает одновременное разрешение после нек-рого конченого накрытия ее базы, причем группой Галуа этого накрытия служит группа Вейля соответствующей корневой системы (см. [5], с. 179-203).
является разрешением особенностей. Нереальная деформация простых О. т. (см. ниже) допускает одновременное разрешение после нек-рого конченого накрытия ее базы, причем группой Галуа этого накрытия служит группа Вейля соответствующей корневой системы (см. [5], с. 179-203).
Особые точки комплексной гиперповерхности. Пусть гиперповерхность Xзадана в  одним уравнением f(x0,...,xn)=0, где f - многочлен (или росток аналитич. ции в точке 0). Якобиевым идеалом многочлена f наз. идеал
одним уравнением f(x0,...,xn)=0, где f - многочлен (или росток аналитич. ции в точке 0). Якобиевым идеалом многочлена f наз. идеал  в кольце
в кольце  {х 0,...,х п};изолированность О. т. О эквивалентна конечномерности пространства
{х 0,...,х п};изолированность О. т. О эквивалентна конечномерности пространства  {х 0,...,xn}/J(f). Размерность m этого пространства наз. числом Милнора многочлена f и совпадает с рангом свободной абелевой группы
{х 0,...,xn}/J(f). Размерность m этого пространства наз. числом Милнора многочлена f и совпадает с рангом свободной абелевой группы 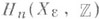 , где
, где 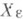 задается уравнением
задается уравнением  , при малых
, при малых  . Более точно, многообразие
. Более точно, многообразие  гомотопически эквивалентно букету m сфер размерности п(см. [12]). База версальной деформации этой особенности неособая и также имеет размерность
гомотопически эквивалентно букету m сфер размерности п(см. [12]). База версальной деформации этой особенности неособая и также имеет размерность  (см. [9]). Простейшим примером является невырожденная квадратичная особенность
(см. [9]). Простейшим примером является невырожденная квадратичная особенность  +...+
+...+  =0. для нее
=0. для нее 
Простой О. т. гиперповерхности наз. особенность, при деформации к-poй появляется лишь конечное число других особенностей [9]; гиперповерхность при этом задается одним из следующих уравнений:
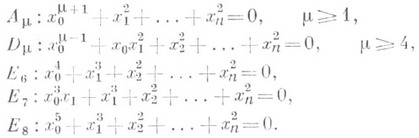
Нижний индекс m здесь - число Милнора особенности. В случае поверхностей ( п=2).эти особенности наз. особенностями дю Валя, или двойными рациональным и О. т. Эти О. т. можно также охарактеризовать тем, что форма пересечения на пространстве 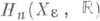 является определенной. Имеется классификация следующих по сложности, унимодальных особенностей [9]. Изучается вещественный аналог этих понятий, а также их связь с теорией катастроф [10]. Многие теоремы об О. т. гиперповерхностей распространяются на О. т. полных пересечений.
является определенной. Имеется классификация следующих по сложности, унимодальных особенностей [9]. Изучается вещественный аналог этих понятий, а также их связь с теорией катастроф [10]. Многие теоремы об О. т. гиперповерхностей распространяются на О. т. полных пересечений.
Особые точки кривых. Пусть А - локальное кольцо О. т. хкривой, а  - его нормализация; главным инвариантом О. т. является
- его нормализация; главным инвариантом О. т. является  . Для неприводимой кривой Xее арифметич. род равен геометрич. роду плюс
. Для неприводимой кривой Xее арифметич. род равен геометрич. роду плюс 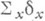 (суммирование по всем О. т. кривой X). Причем для плоской кривой
(суммирование по всем О. т. кривой X). Причем для плоской кривой 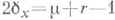 , где m - число Милнора, а r- число ветвей кривой в точке х.
, где m - число Милнора, а r- число ветвей кривой в точке х.
Пусть  - плоская неприводимая кривая, имеющая в точке 0 особенность кратности п(см. Кратность особой точки). Тогда Xдопускает параметризацию
- плоская неприводимая кривая, имеющая в точке 0 особенность кратности п(см. Кратность особой точки). Тогда Xдопускает параметризацию 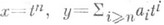 , к-рая записывается в виде
, к-рая записывается в виде

(разложение Пюизё). Характеристич. показателями этого разложения наз. числа
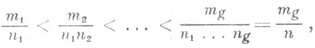
где  - первый нецелый показатель в разложении Пюизё,
- первый нецелый показатель в разложении Пюизё, 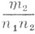 -первый показатель некратный
-первый показатель некратный  и т. д.
и т. д.
Последовательность  , где
, где 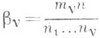
наз. характеристикой особенности. Плоские одномерные особенности топологически эквивалентны тогда и только тогда, когда их характеристики совпадают (см. [8]).
Особые точки поверхностей. Среди разрешений особенностей нормальных поверхностей однозначно выделяются минимальные разрешения p : 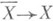 , через к-рые пропускаются все остальные разрешения. Если х - О. т. поверхности X, то кривая
, через к-рые пропускаются все остальные разрешения. Если х - О. т. поверхности X, то кривая  наз. исключительной. Комбинаторным инвариантом О. т. хявляется взвешенный граф Г кривой А, вершины которого соответствуют неприводимым компонентам А i кривой А, точки пересечения компонент А i и А j изображаются ребрами между соответствующими вершинами, вершине приписывается вес, равный роду кривой А i, а иногда еще
наз. исключительной. Комбинаторным инвариантом О. т. хявляется взвешенный граф Г кривой А, вершины которого соответствуют неприводимым компонентам А i кривой А, точки пересечения компонент А i и А j изображаются ребрами между соответствующими вершинами, вершине приписывается вес, равный роду кривой А i, а иногда еще
и индекс самопересечения 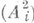 . Матрица
. Матрица 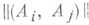 пересечений компонент кривой Аотрицательно определена, граф Г связен. Наименьший положительный дивизор
пересечений компонент кривой Аотрицательно определена, граф Г связен. Наименьший положительный дивизор  такой, что
такой, что  для всех i, наз. фундаментальным циклом особенности. Он всегда существует, и его арифметич. род
для всех i, наз. фундаментальным циклом особенности. Он всегда существует, и его арифметич. род 
неотрицателен. О. т. рациональна тогда и только тогда, когда р(Z)=0 в этом случае кратность ее равна - (Z2), а размерность касательного пространства Зариского на единицу больше [1]. Исследуются также [71 эллиптические особенности (то есть О. т. cp(Z)=l). Лит.:[1] Artin М., "Amer. J. Math.", 1966, v. 68, p. 129-36; 12] Groupes de nionodromie en geometric algebrique, B.- Hdlb.- N. Y., 1972; [3] Kempt G., "Invent, math.", 1976, v. 37, p. 229-39; [4] Schlessinger M., "Invent, math.", 1971, v. 14, p. 17-26; [5] Seminaire sur les singularites des surfaces, В.-Hdlb.-N. Y., 1980; [6] Toroidal embeddings, [v. 1], В.- Hdlb.-N. Y., 1973; [7] Yau S. S.-Т., "Trans. Amer. Math. Soc.", 1980, V. 257, p. 269-329; [8] Zariski O., "Amer. J. Math.", 1968, v. 90, p. 961 - 1023; [9] Apнольд В. И., "Успехи матем. наук", 1975, т. 30, в. 5, с. 3-65; [10] Голубицкий М., Гийемин В., Устойчивые отображения и их особенности, пер. с англ., М., 1977; [11] Гриффите Ф., Xаррис Дж., Принципы алгебраической геометрии, пер. с англ., т. 1-2, М., 1982; [12] Милнор Дж., Особые точки комплексных гиперповерхностей, пер. с англ., М., 1971; [13] Хиронак а X., "Математика", 1965, т. 9, № 6, с. 2-70; 1966, т. 10, № 1, с. 3-89. В. Я. Данилов.
3) О. т. векторного поля X - точка а, для к-рой Х(а)=0. О. т. наз. изолированной, если Xне обращается в нуль в отличных от аточках достаточно малой окрестности точки а. О. т. наз. невырожденной, если

Невырожденная О. т. всегда изолирована.
М. И. Войцеховский,
4) О. т. дифференциального уравнения
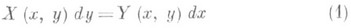
- любая точка 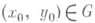 , удовлетворяющая условию
, удовлетворяющая условию

здесь  - непрерывные в иск-рой области
- непрерывные в иск-рой области  функции. Точки области G, не удовлетворяющие условию (2), наз. обыкновенными точками уравнения (1). Иногда точку
функции. Точки области G, не удовлетворяющие условию (2), наз. обыкновенными точками уравнения (1). Иногда точку  наз. О. т. уравнения (1) и в том случае, когда условие (2) не выполняется, но задача Коши для уравнения (1) с начальными данными (x0, y0) имеет более одного решения.
наз. О. т. уравнения (1) и в том случае, когда условие (2) не выполняется, но задача Коши для уравнения (1) с начальными данными (x0, y0) имеет более одного решения.
Уравнение (1) - частный случай системы дифференциальных уравнений в симметричной форме:

где  , функции Х[:
, функции Х[: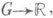 i=1, 2,...,n, непрерывны в нек-рой области
i=1, 2,...,n, непрерывны в нек-рой области 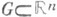 Точка
Точка  наз. особой точкой системы (3), если Х i(x0)=0, i=l,..., п. В противном случае x0 - обыкновенная точка этой системы.
наз. особой точкой системы (3), если Х i(x0)=0, i=l,..., п. В противном случае x0 - обыкновенная точка этой системы.
Пусть Н - множество О. т. системы (3) в области G. Если 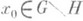 , то существуют индекс
, то существуют индекс  и окрестность Uточки x0 такие, что в Uсистема (3) представима в нормальной форме:
и окрестность Uточки x0 такие, что в Uсистема (3) представима в нормальной форме:

Таким образом, поведение интегральных кривых системы (3) в окрестности обыкновенной точки описывается теоремами общей теории обыкновенных дифференциальных уравнений. В частности, справедлива следующая теорема о выпрямлении: если через любую точку х 0 множества  проходит единственная интегральная кривая системы (3), то каждая точка этого множества имеет окрестность Vтакую, что семейство дуг интегральных кривых системы (3), заполняющих V, гомеоморфно (а если
проходит единственная интегральная кривая системы (3), то каждая точка этого множества имеет окрестность Vтакую, что семейство дуг интегральных кривых системы (3), заполняющих V, гомеоморфно (а если  , i=l,..., п, то диффеоморфно) семейству параллельных прямых.
, i=l,..., п, то диффеоморфно) семейству параллельных прямых.
Если же 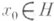 , то пары (i0, U), обладающей указанным выше свойством, не существует, и интегральные кривые системы (3) могут образовывать вблизи х 0 различные конфигурации. Так, для уравнения
, то пары (i0, U), обладающей указанным выше свойством, не существует, и интегральные кривые системы (3) могут образовывать вблизи х 0 различные конфигурации. Так, для уравнения
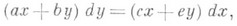
где 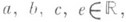 а матрица
а матрица  - невырожденная, расположение интегральных кривых в окрестности точки (0, 0) может относиться к типу седло, узел, центр пли фокус. Соответствующее название закрепляется при атом и за самой точкой (0, 0).
- невырожденная, расположение интегральных кривых в окрестности точки (0, 0) может относиться к типу седло, узел, центр пли фокус. Соответствующее название закрепляется при атом и за самой точкой (0, 0).
Систему (3) можно рассматривать как результат исключения времени tиз автономной системы дифференциальных уравнений
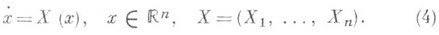
Если (4) - система класса ( , единственность) в G, то есть
, единственность) в G, то есть  , и через каждую точку области G проходит единственная траектория системы, что далее и предполагается, то точки множества Нбудут для нее точками покоя ( равновесия положениями). Часто их наз. О. т. и для этой системы, поскольку они являются таковыми (по определению) для векторного поля X. Интегральные кривые системы (3), расположенные в
, и через каждую точку области G проходит единственная траектория системы, что далее и предполагается, то точки множества Нбудут для нее точками покоя ( равновесия положениями). Часто их наз. О. т. и для этой системы, поскольку они являются таковыми (по определению) для векторного поля X. Интегральные кривые системы (3), расположенные в  , представляют собою траектории системы (4), отличные от состояний покоя.
, представляют собою траектории системы (4), отличные от состояний покоя.
Таким образом, задачи о поведении интегральных кривых системы (3) в окрестности О. т. и о расположении траекторий системы (4) в окрестности положений равновесия эквивалентны. Исследования этих задач ведутся по двум основным направлениям.
Одно направление, берущее свое начало в трудах А. Пуанкаре [1], ставит своей целью выяснение возможных топологич. типов расположения траекторий системы (4) в окрестности изолированной точки покоя (к-рую всегда ложно считать совпадающей с началом координат 0( х=0)). и отыскание аналитич. ритериев их различения. Наиболее законченные результаты получены здесь для того случая, когда система (4) представима в виде

где А - постоянная невырожденная матрица, f(x).о(||x||) при 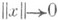 . В этом случае точка Оназ. простой, или невырожденной, особой точкой системы (4). Для системы (5) установлена следующая теорема о топологической эквивалентности: если матрица Ане имеет чисто мнимых собственных значений, а функция
. В этом случае точка Оназ. простой, или невырожденной, особой точкой системы (4). Для системы (5) установлена следующая теорема о топологической эквивалентности: если матрица Ане имеет чисто мнимых собственных значений, а функция 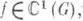 то существует гомеоморфизм hокрестности Uточки Она окрестность Vтой же точки, переводящий траектории системы (5) в траектории линейной системы
то существует гомеоморфизм hокрестности Uточки Она окрестность Vтой же точки, переводящий траектории системы (5) в траектории линейной системы

Гомеоморфизм  , осуществляющий топологич. соответствие между траекториями систем (5) и (6), в общем случае не является (и не может быть заменен) диффеоморфизмом.
, осуществляющий топологич. соответствие между траекториями систем (5) и (6), в общем случае не является (и не может быть заменен) диффеоморфизмом.
При условиях этой теоремы точка покоя Осистемы (5) относится к тому же топологич. типу, что и точка покоя Осистемы (6). В частности, для системы 2-го порядка она будет при этом седлом, если собственные значения l1,l2 матрицы Аудовлетворяют условию l1l2<0, топологическим узлом (узлом или фокусом), если l1l2>0 (при чисто мнимых l1,l2 точка Одля системы (6) - центр, а для системы (5) - центр, фокус или центро-фокус).
Если матрица Аимеет чисто мнимые или нулевые собственные значения, то топологич. эквивалентности между системами (5) и (6) в окрестности точки Ов общем случае нет. При этих условиях поведение траекторий системы (5) в окрестности точки Овесьма детально изучено в тех случаях, когда матрица Аимеет не более двух собственных значений с нулевыми действительными частями, а функция f - аналитическая. В частности, для системы 2-го порядка с ненулевой матрицей Авыяснены все возможные топологич. типы расположения траекторий в окрестности точки Ои даны коэффициентные критерии их различения с точностью до различения центра и фокуса [9]. Здесь, кроме седла, топологич. узла и центра, точка Оможет быть: двухсепаратрисным седлом, седло-узлом (некрая окрестность Uточки Оразбивается тремя примыкающими к Отраекториями (сепаратрисами) на три сектора: два гиперболических, заполненных траекториями, к-рые обоими концами покидают U, и один параболический, заполненный траекториями, к-рые одним концом покидают U, а другим примыкают к О).и точкой (нек-рая ее окрестность Uразбивается сепаратрисами на 4 сектора: один гиперболический, два параболических и один эллиптический, заполненный траекториями, к-рые обоими концами примыкают к О, охватывая друг друга). Для системы 2-го порядка с нулевой матрицей Аразработаны алгоритмы расщепления особенности (см., напр., Фроммера метод), позволяющие с помощью конечного числа шагов процесса расщепления выяснить тоиологич. тип точки Ос точностью до решения задачи о различении центра и фокуса. Последняя задача (см. Центра и фокуса проблема).возникает для системы 2-го порядка вида (5) в случае, когда матрица Аимеет чисто мнимые собственные значения, и может возникать в случае двух нулевых собственных значении этой матрицы. Она решена для частных классов таких систем.
Важной характеристикой изолированной точки покоя Осистемы (4) является ее индекс Пуанкаре. Для п =2 он определяется как вращение векторного ноля Xпри обходе точки Опо окружности  достаточно малого радиуса р в положительном направленпп, измеренной в единицах полного оборота. Напр., индекс простого седла равен -1, индекс узла, фокуса и центра равен 1. При произвольном пиндекс точки Оопределяется как стеиенг, отображения hсферы
достаточно малого радиуса р в положительном направленпп, измеренной в единицах полного оборота. Напр., индекс простого седла равен -1, индекс узла, фокуса и центра равен 1. При произвольном пиндекс точки Оопределяется как стеиенг, отображения hсферы  достаточно малого радиуса р на себя, определенного формулой:
достаточно малого радиуса р на себя, определенного формулой:

Это направление развилось в обширную качественную теорию дифференциальных уравнений, а центр тяжести исследований переместился с локальных проблем на глобальные - изучение поведения траекторий системы (4) во всей области задания G, к-рая все чаще предполагается гладким многообразием той или иной природы.
Другое направление, заложенное трудами А. М. Ляпунова [2], занимается исследованном решений (в частности, состояний равновесия) систем вида (4), а также неавтономных систем дифференциальных уравнений на устойчивость. Оно представляет собою разветвленную теорию устойчивости движения (см. Устойчивости теория).
В комплексном анализе вводится понятие О. т. дифференциального уравнения

а также системы дифференциальных уравнений

где z - комплексная переменная, Р - рациональная функция от w, w', . . ., w(n-1) или от компонент w1,w2,...,wn вектора  , коэффициенты к-рой - известные аналитич. ции от z. Особой для уравнения (7) (системы (8)) наз. любая точка z0 комплексной плоскости, к-рая является О. т. хотя бы одного из коэффициентов функции Р(см. Особая точка аналитической функции). О. т. уравнения или системы, как правило, являются особыми и для их решений как аналитич. ций от z. Они наз. неподвижными особами точками решений. Кроме того, решения уравнения (7) (системы (8)) могут иметь подвижные особые точки, положение к-рых определяется начальными данными решений. Исследование различных классов уравнений вида (7), (8) с целью изучения аналитич. рироды решений в окрестности особых точек уравнений и с целью выяснения вопроса о наличии у решений этих уравнений подвижных О. т. различных типов составляет предмет аналитической теории дифференциальных уравнений.
, коэффициенты к-рой - известные аналитич. ции от z. Особой для уравнения (7) (системы (8)) наз. любая точка z0 комплексной плоскости, к-рая является О. т. хотя бы одного из коэффициентов функции Р(см. Особая точка аналитической функции). О. т. уравнения или системы, как правило, являются особыми и для их решений как аналитич. ций от z. Они наз. неподвижными особами точками решений. Кроме того, решения уравнения (7) (системы (8)) могут иметь подвижные особые точки, положение к-рых определяется начальными данными решений. Исследование различных классов уравнений вида (7), (8) с целью изучения аналитич. рироды решений в окрестности особых точек уравнений и с целью выяснения вопроса о наличии у решений этих уравнений подвижных О. т. различных типов составляет предмет аналитической теории дифференциальных уравнений.
Лит.:[1] Poincare IL, Sur les courbcs definies par unc equation differentiellc, Oeuvres, t. 1, P., 1892; рус. пер.- Пyанкаре А., О кривых, определяемых дифференциальными уравнениями, М.- Л., 1947; [2] Ляпунов А., Общая задача об устойчивости движения, М.- Л., 1950; [3] Немыцкий В. В., Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М.- Л., 1949; [4] Коддингтон 9. А., Левин со п Н., Теория обыкновенных дифференциальных уравнений, пер. сангл.,М., 1958; [5] Лефшец С., Геометрическая теория дифференциальных уравнений, пер. с англ., М., 1961; [6] Sansоnе О., Сеnti R., Non-linear differential equations, Oxf., 1964; [7] Хартман Ф., Обыкновенные дифференциальные уравнения, пер. с англ., М., 1970; [8] Арнольд В. И., Обыкновенные дифференциальные уравнения, М.,1971; [9] Баутин Н. Н., ЛеонтовичЕ. А., Методы и приемы качественного исследования динамических систем на плоскости, М., 1976; [10] Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, 2 изд., М.- Л., 1950; [11] Еругин Н. П., Книга для чтения по общему курсу дифференциальных уравнений, 2 изд., Минск, 1972; [12] Брюно А. Д., Локальный метод нелинейного анализа дифференциальных уравнений, М., 1979: [13] Андреев А. Ф., Особые точки дифференциальных уравнений, Минск, 1979.
А. Ф. Андреев.
5) О. т. дифференцируемого отображения f - точка, к-рая является для f нерегулярной (критической) и неправильной одновременно. Точнее, пусть М т и Nn- два дифференцируемых многообразия размерностей ти псоответственно, а  Nn- дифференцируемое отображение первого во второе, х i и yi=f(xj)- локальные координаты в них.
Nn- дифференцируемое отображение первого во второе, х i и yi=f(xj)- локальные координаты в них.
Если ранг матрицы в точке ,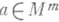 равен т,
равен т,
то отображение f наз.  регулярным в точке
регулярным в точке
а. Если ранг матрицы  равен пв точке
равен пв точке 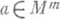 , то отображение f наз. правильным в точке а. В О. т. f ранг этой матрицы меньше обоих чисел т и н. См. также Особенности дифференцируемых отображений. М. И. Войцеховский.
, то отображение f наз. правильным в точке а. В О. т. f ранг этой матрицы меньше обоих чисел т и н. См. также Особенности дифференцируемых отображений. М. И. Войцеховский.
6) О. т. действительной кривой F(x,y)=0- точка ( х 0, у 0), в к-рой первые частные производные равны нулю (F'x)0=0,(F'y)0=0. О. т. наз. двоиной точкой, если по крайней мере одна из вторых частных производных функции F(x, у).не равна нулю. При исследовании строения кривой в окрестности О. т. рассматривают знак выражения

Если D>0, то О. т. является изолированной точкой (см. рис. , а); узловой точкой (или точкой самопересечения), если D<0 (см. рис.., б); если D=0, то О. т. является либо изолированной точкой, либо характеризуется тем, что различные ветви кривой имеют в этой точке общую касательную. Если ветви кривой расположены по разные стороны от общей касательной и по одну сторону от общей нормали, то О. т. наз. точкой возврата 1-го рода (см. рис. , в); если ветви кривой расположены по одну сторону от общей касательной и по одну сторону от общей нормали, то О. т. наз. точкой возврата 2-го рода (см. рис. , г); если ветви расположены по разные стороны от общей нормали и по разные стороны от общей касательной (см. рис. , д).или по одну сторону от общей касательной и по разные стороны от общей нормали (см. рис..,, е), то О. т. наз. точкой самоприкосновения. См. также Двойная точка.
Если в нек-рой точке все частные производные от функции F(x, у).до (k-1)-ro порядка включительно обращаются в нуль, а среди производных k-го порядка по крайней мере одна отлична от нуля, то эта точка наз. особой точкой k - гопорядка (кратной точкой).
Иногда О. т. наз. точки, отличающиеся каким-либо свойством от других точек кривой; см., напр., Перегиба точка, Прекращения точка, Излома точка, Спрямления точка, Уплощения точка.
О. т. пространственной кривой, заданной уравнениями F(x, у,z)=0, G(x, y, z)=0 - точка, в окрестности к-рой ранг матрицы
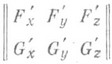
меньше двух.
Лит.:[1] Рашевский II. К., Курс дифференциальной геометрии, 4 изд.,-М., 1956; [2] Бюшгенс С. С., Дифференциальная геометрия, т. 1, М.- Л., 1940; [3] Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М.- Л., 1969. А. Б. Иванов.
7) О. т. действительной поверхности- точка поверхности х=х( и, v), y=y(u, v), z=z(u, v), в к-рой ранг матрицы

меньше двух. Если поверхность определяется как множество точек, координаты к-рых удовлетворяют уравнению F(x, у, z)=0, то О. т. наз. точку (x0, у 0, z0) поверхности, в к-poй первые частные производные функции F(x, у, z).равны нулю:

Если в О. т. не все вторые частные производные функции F(x, у, z) обращаются в нуль, то касательные к поверхности в О. т. образуют конус. Если конус касательных невырожденный, то О. т. наз. конической точной; если конус вырождается в две

действительные плоскости, то О. т. является точкой само пересечения поверхности; если конус мнимый, то О. т.- изолированная точка поверхности.
О. т. могут составлять т. н. особые линии поверхности: возврата ребро, линии самопересечения, самоприкосновения и др.
Лит.: [1]Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; [2] Норден А. П., Краткий курс дифференциальной геометрии, 2 изд., М., 1958; [3] Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., ч. 2, М., 1980. А. В. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.