Akademik

- метрика пространства, задаваемая положительно определенной квадратичной формой. Если в пространстве V_n введена локальная система координат (x¹, ... , х ⁿ )и в каждой точке Х(х ¹, ... , ... , х ⁿ)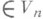 определены функции g_ij(X), i, j=1, 2, ... , n, det (g_ij)>0, g_ij(X)=g_ji(X), являющиеся компонентами ковариантного симметричного тензора второй валентности, то этот тензор наз. о с н о в н ы м м е тр и ч е с к и м т е н з о р о м пространства V_n. С помощью основного тензора выражается длина ds контравариантного вектора (dx¹,... , dxⁿ):

форма является положительно определенной квадратичной формой. Метрика пространства V_n , определенная с помощью формы ds², наз. римановой, а пространство с введенной в нем Р. м. наз. римановым пространством. Задание Р. м. на нек-ром дифференцируемом многообразии означает задание на этом многообразии евклидовой структуры, дифференцируемым образом зависящей от точки.

Р. м. является обобщением первой квадратичной формы поверхности в трехмерном евклидовом пространстве - внутренней метрики поверхности. Геометрия пространства V_n , основанная на определенной Р. м., наз. римановой геометрией.

Существуют обобщения понятия Р. м. Так, псевдориманова метрика определяется с помощью неопределенной квадратичной формы (см. Псевдориманово пространство и Относительности теория). Вырожденная Р. м., то есть метрич. форма, определенная с помощью функций g_ij(X), для к-рых det (g_ij) = 0, определяет нек-рое полуриманово пространство.

Лит.:[1] Э й з е н х а р т Л. П., Риманова геометрия, пер. с англ., М., 1948; [2] Р а ш е в с к и й П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; [3] Р и м а н Б., О гипотезах, лежащих в основании геометрии, пер. с нем., в кн.: Об основаниях геометрии, М., 1956. Л. А. Сидоров.