конечномерное пространство 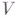 , удовлетворяющее условию: если
, удовлетворяющее условию: если 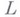 - Ли алгебра над полем
- Ли алгебра над полем 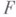 , а
, а 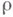 - ее представление в V, то существует такая функция
- ее представление в V, то существует такая функция 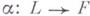 , что для любых
, что для любых 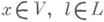
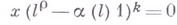
при нек-ром целом 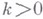 . Функция
. Функция 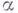 наз. весом. Тензорное произведение
наз. весом. Тензорное произведение  представлений
представлений  алгебры Lв В. п.
алгебры Lв В. п. 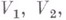 принадлежащих весам
принадлежащих весам 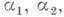 соответственно, является представлением Lв пространстве
соответственно, является представлением Lв пространстве  к-рое также оказывается В. п. и принадлежит весу i
к-рое также оказывается В. п. и принадлежит весу i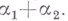 При переходе от представления р к контраградиентному представлению
При переходе от представления р к контраградиентному представлению 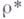 пространство Vзаменяется на сопряженное пространство
пространство Vзаменяется на сопряженное пространство 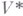 , а вес
, а вес 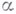 переходит в вес -
переходит в вес -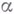 . Е. Н. Кузьмин. ВЕТВЛЕНИЕ РЕШЕНИЙ нелинейных уравнений- явление перехода нек-рого решения нелинейного уравнения в несколько решений (или полное его исчезновение) при малых изменениях параметров. Более точно, пусть нелинейное уравнение
. Е. Н. Кузьмин. ВЕТВЛЕНИЕ РЕШЕНИЙ нелинейных уравнений- явление перехода нек-рого решения нелинейного уравнения в несколько решений (или полное его исчезновение) при малых изменениях параметров. Более точно, пусть нелинейное уравнение

с (не обязательно числовым) параметром 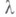 имеет при фиксированном значении
имеет при фиксированном значении 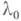 решение
решение 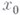 . Тогда при значениях
. Тогда при значениях 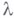 , близких к
, близких к 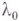 , уравнение (*) может иметь несколько (более одного) решений
, уравнение (*) может иметь несколько (более одного) решений 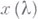 , близких к
, близких к 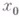 .
.
В этих случаях говорят, что происходит ветвление решения 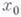 ,а пара
,а пара 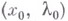 наз. точкой ветвления у равнения (*).
наз. точкой ветвления у равнения (*).
Пример: Уравнение 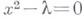 , где
, где 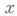 и
и 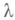 - комплексные переменные, имеет точку ветвления
- комплексные переменные, имеет точку ветвления 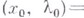
 ибо существует двузначное решение
ибо существует двузначное решение 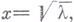 т. е. решение
т. е. решение  (при
(при 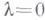 ) разветвляется при малых
) разветвляется при малых 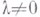 на два малых нетривиальных решения.
на два малых нетривиальных решения.
Современная теория В. р. основывается на идеях А. М. Ляпунова [1] и Э. Шмидта [2] и наиболее развита для нелинейных уравнений в банаховых пространствах.
Пусть 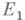 и
и 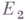 - комплексные банаховы пространства,
- комплексные банаховы пространства, 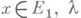 - комплексное переменное, а
- комплексное переменное, а 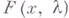 - нелинейный оператор, непрерывный вместе с Фреше производной
- нелинейный оператор, непрерывный вместе с Фреше производной 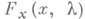 в окрестности
в окрестности 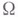 точки
точки 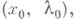 отображающий
отображающий 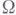 в окрестность нуля пространства E2 п такой, что
в окрестность нуля пространства E2 п такой, что 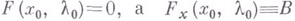 - Фредгольма оператор.
- Фредгольма оператор.
Задача состоит в том, чтобы найти в шаре 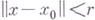 достаточно малого радиуса rвсе решения уравнения (*), непрерывные при
достаточно малого радиуса rвсе решения уравнения (*), непрерывные при 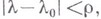 где
где 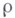 также достаточно мало. Иными словами, это есть задача локального продолжения решения
также достаточно мало. Иными словами, это есть задача локального продолжения решения 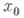 по параметру
по параметру 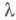 . Если существует обратный оператор
. Если существует обратный оператор 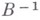 , то задача имеет единственное решение
, то задача имеет единственное решение 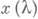 , причем
, причем 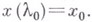 Если же
Если же 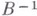 , не существует, то нуль-пространство
, не существует, то нуль-пространство 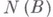 оператора Вимеет размерность
оператора Вимеет размерность  . В этом случае задача может быть сведена к аналогичной конечномерной задаче. Пусть через Робозначен проектор
. В этом случае задача может быть сведена к аналогичной конечномерной задаче. Пусть через Робозначен проектор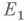 на
на 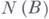 , а через
, а через 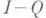 - проектор
- проектор 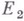 на область значений оператора В, где I - тождественный оператор. Уравнение (*) может быть записано в виде системы
на область значений оператора В, где I - тождественный оператор. Уравнение (*) может быть записано в виде системы

где 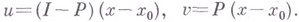 Из первого уравнения системы определяется неявный оператор
Из первого уравнения системы определяется неявный оператор 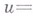
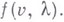 В результате его подстановки во второе уравнение системы получается уравнение
В результате его подстановки во второе уравнение системы получается уравнение
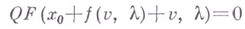
для определения 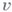 ; оно наз. уравнением разветвления. Полное решение задачи о нахождении в шаре
; оно наз. уравнением разветвления. Полное решение задачи о нахождении в шаре 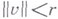 достаточно малого радиуса rвсех решений
достаточно малого радиуса rвсех решений 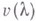 уравнения разветвления, непрерывных при
уравнения разветвления, непрерывных при 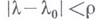 (где
(где 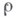 достаточно мало), приводит к полному решению исходной задачи, ибо всякое ее решение пред-ставимо в виде
достаточно мало), приводит к полному решению исходной задачи, ибо всякое ее решение пред-ставимо в виде
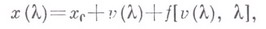
где 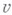 - нек-рое решение уравнения разветвления.
- нек-рое решение уравнения разветвления.
Пусть 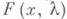 - аналитический оператор в
- аналитический оператор в  . Выбор базисов в и-мерных подпространствах
. Выбор базисов в и-мерных подпространствах 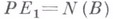 и
и 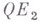 позволяет записать уравнение разветвления в виде системы
позволяет записать уравнение разветвления в виде системы
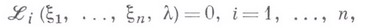
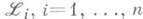 - аналитич. функции в точке
- аналитич. функции в точке 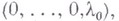 причем все частные производные
причем все частные производные 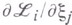 обращаются в нуль в этой точке. Исследование этой системы может осуществляться при помощи теории исключения, метода Ньютона диаграммы п др. методов (см. [3] - [5]). При n=1 полный анализ осуществляется методом диаграммы Ньютона. Применительно к исследованию уравнения разветвления, а значит и исходной задачи, возможны лишь следующие три случая: а) задача не имеет решений; б) задача имеет конечное число решений и все ени представимы сходящимися рядами по целым или дробным степеням разности
обращаются в нуль в этой точке. Исследование этой системы может осуществляться при помощи теории исключения, метода Ньютона диаграммы п др. методов (см. [3] - [5]). При n=1 полный анализ осуществляется методом диаграммы Ньютона. Применительно к исследованию уравнения разветвления, а значит и исходной задачи, возможны лишь следующие три случая: а) задача не имеет решений; б) задача имеет конечное число решений и все ени представимы сходящимися рядами по целым или дробным степеням разности 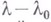 ; в) задача имеет конечное число семейств решений, каждое из к-рых зависит от конечного числа свободных малых параметров, и, быть может, конечное число решений, указанных в б).
; в) задача имеет конечное число семейств решений, каждое из к-рых зависит от конечного числа свободных малых параметров, и, быть может, конечное число решений, указанных в б).
Для того чтобы имел место случай б), достаточно, чтобы 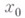 было изолированным решением уравнения
было изолированным решением уравнения 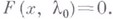 В случае б) решения удобно искать методом неопределенных коэффициентов в виде
В случае б) решения удобно искать методом неопределенных коэффициентов в виде
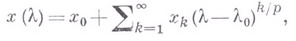
где 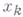 - коэффициенты, подлежащие определению, а возможные значения рмогут быть предварительно найдены с помощью уравнения разветвления. Подстановка такого ряда в (*) приводит к рекуррентной системе для нахождения
- коэффициенты, подлежащие определению, а возможные значения рмогут быть предварительно найдены с помощью уравнения разветвления. Подстановка такого ряда в (*) приводит к рекуррентной системе для нахождения 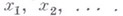 При этом получаются задачи вида
При этом получаются задачи вида 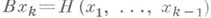 и каждое xk определяется с точностью до ппроизвольных постоянных, к-рые определяются из требований разрешимости последующих уравнений. Все полученные ряды сходятся в нек-рой окрестности точки
и каждое xk определяется с точностью до ппроизвольных постоянных, к-рые определяются из требований разрешимости последующих уравнений. Все полученные ряды сходятся в нек-рой окрестности точки 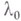 . Оценка снизу радиуса окрестности может быть получена с помощью построения мажорант (см. [6]).
. Оценка снизу радиуса окрестности может быть получена с помощью построения мажорант (см. [6]).
Для того чтобы имел место случай в), необходимо, чтобы 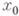 было неизолированным решением уравнения
было неизолированным решением уравнения 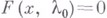 . Здесь применение метода неопределенных коэффициентов может привести к расходящимся рядам (формальным решениям). Если задача инвариантна относительно непрерывной группы линейных операторов в
. Здесь применение метода неопределенных коэффициентов может привести к расходящимся рядам (формальным решениям). Если задача инвариантна относительно непрерывной группы линейных операторов в 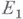 , то в ряде случаев использование групповых соображений позволяет уменьшить число уравнений и неизвестных в уравнении разветвления и тем самым упростить задачу или даже свести ее к случаю б) (см. [7], [8]). .
, то в ряде случаев использование групповых соображений позволяет уменьшить число уравнений и неизвестных в уравнении разветвления и тем самым упростить задачу или даже свести ее к случаю б) (см. [7], [8]). .
Уравнение  может иметь также решения, определенные лишь при
может иметь также решения, определенные лишь при 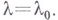 Эти решения возможны только тогда, когда
Эти решения возможны только тогда, когда 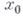 - неизолированное решение уравнения
- неизолированное решение уравнения 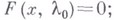 они находятся при помощи уравнения разветвления при
они находятся при помощи уравнения разветвления при 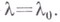 Определение всех его многопараметрич. семейств решений приводит к определению всех решений уравнения (*) с
Определение всех его многопараметрич. семейств решений приводит к определению всех решений уравнения (*) с 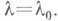
В случае вещественных пространств 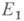 и
и 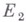 уравнение разветвления изучается в комплексной области, а затем отбираются вещественные решения. Нек-рые из них могут оказаться определенными в полуокрестностях точки
уравнение разветвления изучается в комплексной области, а затем отбираются вещественные решения. Нек-рые из них могут оказаться определенными в полуокрестностях точки 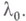
Изложенная методика частично применима также в случаях, когда 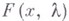 - достаточно гладкий оператор, В - нётеров оператор, а параметр
- достаточно гладкий оператор, В - нётеров оператор, а параметр 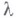 - элемент еще одного банахова пространства Е(точки ветвления могут заполнять в Елинии и поверхности). Этим же способом исследуются нек-рые близкие задачи: задача отыскания больших решений (уравнение (*) может иметь решения
- элемент еще одного банахова пространства Е(точки ветвления могут заполнять в Елинии и поверхности). Этим же способом исследуются нек-рые близкие задачи: задача отыскания больших решений (уравнение (*) может иметь решения  при
при  ), задача ветвления собственных значений и собственных элементов линейных операторов и др. (см. [3]). Частный случай, когда
), задача ветвления собственных значений и собственных элементов линейных операторов и др. (см. [3]). Частный случай, когда
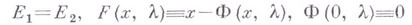
исследовался также топологическими, вариационными методами и методами, использующими конусы в банаховом пространстве. В этом круге вопросов значительную роль играет понятие точки бифуркации. Встречаются также задачи о ветвлении решений, не укладывающиеся в описанную выше схему. Это, напр., задачи для дифференциальных уравнений с вырождением (см. [9], [10]) и задачи о длинных и уединенных волнах (см. [11]).
Лит.:[1] Ляпунов А. М., О фигурах равновесия, мало отличающихся от эллипсоидов, вращающейся однородной мяссы жидкости, Собр. соч., т. 4, М., 1959; [2] Sсhmidt E., "Math. Ann.", 1908, Bd 65, S. 370-99; [3] Вайнберг М. М.. Треногий В. А., Теория ветвления решений нелинейных уравнений, М., 1989; 4 Вайнберг М. М., Треногин В. А., "Успехи матем. наук", 1962, т. 17, в. 2: [5] Красносельский М. А. [и д р.], Приближенное решение операторных уравнений, М., 1969; [6] Ахмедов К. Т., "Успехи матем. наук", 1957, т. 12, в. 4, с. 135-53; [7] Юдович В. И., "Прикл. матем. и механ.", 1967, т. 31, в. 1, с. 101 -11; [8] ЛогиновБ. В., Треногий В. А., "Докл. АН СССР", 1971, т. 197, № 1; [9] АхмедовК. Т., там же, 1957, т. 115, № 1;[10] Сидоров Н. А., "Дифференц. уравнения", 1967, т. 3, № 9; [11] Тер-Крикоров А. М., Треногин В. А., там же, т. 3, № 3.
В, А. Треногий.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.