- КЕПЛЕРА ЗАКОНЫ
-
три закона движения планет, открытые нем. астрономом И. Кеплером (J. Kepler) в нач. 17 в. Ниже приведены их совр. формулировки.1-й закон: при невозмущённом движении (в двух тел задаче) орбита движущейся матер. точки (планеты) есть кривая второго порядка, в одном из фокусов к-рой находится центр силы притяжения (Солнце). Т. о., орбита матер. точки в невозмущённом движении — это одно из конич. сечений, т. е. окружность, эллипс (для планет), парабола или гипербола.2-й закон: при невозмущённом движении площадь, описываемая радиусом-вектором движущейся точки, изменяется пропорц. времени (рис.). Часто 2-й закон формулируют как закон площадей: радиус-вектор планеты в равные промежутки времени описывает равные площади.3-й закон: при невозмущённом эллнптич. движении двух матер. точек (планет) вокруг центр. тела (Солнца) произведения квадратов времён обращения на суммы масс центральной и движущейся точек относятся как кубы больших полуосей их орбит, т. е.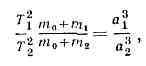
где T1 и T2 — периоды обращения двух точек, m1 и m2 — их массы, m0 — масса центр. точки (Солнца), a1 и а2 — большие полуоси орбит точек (планет). Пренебрегая массами планет m1 и m2 по сравнению с маесой Солнца mсолн, получаем 3-й К. з. в его первонач. форме: квадраты периодов обращений двух планет вокруг Солнца относятся как кубы больших полуосей их эллиптич. орбит. 3-й К. з. в применении к планетам, спутникам планет, компонентам двойных звёзд позволяет подсчитать массы планет, сумму масс двойной звёздной системы (если известны период обращения компонент и параллакс системы), расстояния до двойных систем (т. н. динамич. параллаксы).
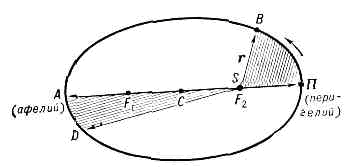Орбита планеты — эллипс: F1 и F2 — фокусы эллипса, в одном из к-рых находится Солнце S; СП=СА — большая полуось орбиты; r — радиус-вектор планеты; отрезки траектории ПВ и AD планета проходит за одинаковое время; площади секторов SПB=SAD.К. з., найденные из наблюдений, были выведены Ньютоном как строгое решение задачи двух тел. Однако в действительности, в результате взаимного влияния планет Солнечной системы, траектории планет — сложные пространств. кривые, к-рые можно интерпретировать как эллиптические лишь за время одного-двух оборотов.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- КЕПЛЕРА ЗАКОНЫ
-
- эмпирич. законы, описывающие движение планет вокруг Солнца. Установлены И. Кеплером (J. Kepler) в нач. 17 в. на основе наблюдений положений планет относительно звёзд.
Первый К. з. Все планеты движутся по эллипсам, в одном из фокусов к-рых находится Солнце.
Второй К. з. Площади, описываемые радиусами-векторами планет, пропорциональны времени.
Третий К. а. Квадраты периодов обращений относятся как кубы их ср. расстояний от Солнца.
Первые два К. з. были опубликованы в 1609, третий - в 1619. К. з. сыграли важную роль в установлении И. Ньютоном закона всемирного тяготения. Решение задачи о движении материальной точки, взаимодействующей по этому закону с неподвижной центр. точкой (невозмущённое кеплеровское движение), приводит к формулировке обобщённых К. з.
1. В невозмущённом движении орбита движущейся точки есть кривая второго порядка, в одном из фокусов к-рой находится центр силы притяжения.
2. В невозмущённом движении площадь, описываемая радиусом-вектором точки, изменяется пропорц. времени.
3. В невозмущённом эллиптич. движении двух точек произведения квадратов времён обращений на суммы масс центральной и движущейся точек относятся как кубы больших полуосей их орбит:
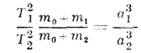
где Т 1 и Т 2 - периоды обращения точек с массами m1 и m2, движущихся вокруг центр. точки с массой т 0 по эллипсам с большими полуосями а2 соответственно. Третий закон, в частности, позволяет приближённо определять массы планет, обладающих спутниками. Пусть спутник с массой m2 обращается по эллипсу с большой полуосью а2 вокруг планеты с массой m1, к-рая, в свою очередь, движется вокруг Солнца по эллиптич. орбите с большой полуосью Т1) и спутника вокруг планеты ( Т2), то при условии m1>m2 из третьего закона можно определить величину m1 в единицах массы Солнца m0:
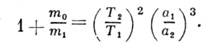
Лит.: Дубошин Г. Н., Небесная механика, 2 изд., М.. 1978. И. А. Герасимов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.