- МАКСВЕЛЛА РАСПРЕДЕЛЕНИЕ
-
распределение по скоростям молекул (ч-ц) макроскопич. физ. системы, находящейся в статистич. равновесии, при условии, что движение молекул подчиняется законам классич. механики (пример — классический идеальный газ). Установлено Дж. Максвеллом в 1859. Согласно М. р., вероятное число молекул в ед. объёма f(v), компоненты скоростей к-рых лежат в интервалах от vx до vx+dvx, от vy до vy+dvy и от vz до vz+dvz, определяются ф-цией распределения Максвелла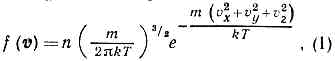 где т — масса молекулы, n — число молекул в ед. объёма. Отсюда следует, что число молекул, абс. значения скоростей к-рых лежат в интервале от v до v+dv, также называемое М. р., имеет вид:
где т — масса молекулы, n — число молекул в ед. объёма. Отсюда следует, что число молекул, абс. значения скоростей к-рых лежат в интервале от v до v+dv, также называемое М. р., имеет вид: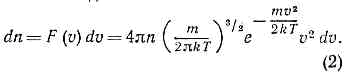 Оно достигает максимума при скорости vb=?(2kT/m) , наз. Наиболее вероятной скоростью. Для мол. водорода при T=273 К vb=1506 м/с. При помощи М. р. можно вычислить ср. значение любой ф-ции от скорости молекулы: ср. скорость vb (рис.).
Оно достигает максимума при скорости vb=?(2kT/m) , наз. Наиболее вероятной скоростью. Для мол. водорода при T=273 К vb=1506 м/с. При помощи М. р. можно вычислить ср. значение любой ф-ции от скорости молекулы: ср. скорость vb (рис.).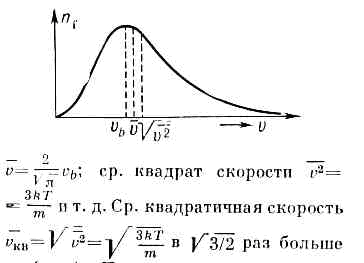 При возрастании темп-ры максимум М. р. (значение vb) смещается к более высоким темп-рам. М. р. не зависит от вз-ствия между молекулами и справедливо не только для газов, но и для жидкостей, если для них возможно классич. описание. Оно справедливо также и для броуновских ч-ц (см. БРОУНОВСКОЕ ДВИЖЕНИЕ), взвешенных в жидкости или газе. М. р. может быть получено из канонического распределения Гиббса для классич. системы интегрированием по всем координатам ч-ц, т. к. в этом случае распределение по скоростям не зависит от распределения по импульсам. М. р. есть решение кинетического уравнения Больцмана для частного случая статистич. равновесия.М. р. было подтверждено экспериментально нем. физиком О. Штерном (1920) в опытах с мол. пучками.
При возрастании темп-ры максимум М. р. (значение vb) смещается к более высоким темп-рам. М. р. не зависит от вз-ствия между молекулами и справедливо не только для газов, но и для жидкостей, если для них возможно классич. описание. Оно справедливо также и для броуновских ч-ц (см. БРОУНОВСКОЕ ДВИЖЕНИЕ), взвешенных в жидкости или газе. М. р. может быть получено из канонического распределения Гиббса для классич. системы интегрированием по всем координатам ч-ц, т. к. в этом случае распределение по скоростям не зависит от распределения по импульсам. М. р. есть решение кинетического уравнения Больцмана для частного случая статистич. равновесия.М. р. было подтверждено экспериментально нем. физиком О. Штерном (1920) в опытах с мол. пучками.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МАКСВЕЛЛА РАСПРЕДЕЛЕНИЕ
-
- распределение по скоростям частиц (молекул) макроскопич. физ. системы, находящейся в статистич. равновесии, в отсутствие внеш. поля при условии, что движение частиц подчиняется законам классич. механики. Установлено Дж. К. Максвеллом (J. С. Maxwell) в 1859. Согласно M. р., вероятное число частиц в единице объёма, компоненты скоростей к-рых лежат в интервалах от Vx до
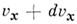 , от
, от 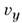 до
до 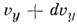 и от
и от 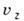 до
до  , равно
, равно 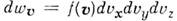 , где
, где 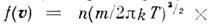
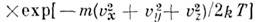 - ф-ция распределения Максвелла по скоростям, n- число частиц в единице объёма, т- масса частицы, T- абс. темп-ра. Отсюда следует, что число частиц, абс. значения скоростей к-рых лежат в интервале от и до u+ du, равно
- ф-ция распределения Максвелла по скоростям, n- число частиц в единице объёма, т- масса частицы, T- абс. темп-ра. Отсюда следует, что число частиц, абс. значения скоростей к-рых лежат в интервале от и до u+ du, равно 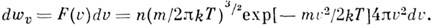
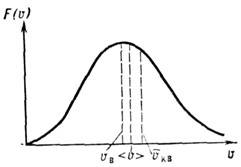
Это распределение наз. M. р. по абс. значениям скоростей. Ф-ция F(V )достигает максимума при скорости
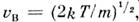 наз. наиб, вероятной скоростью. Для молекул H2 при T -273К uB ~1500 м/с. При помощи M. р. можно вычислить ср. значение любой ф-ции от скорости молекул: ср. квадрат скорости
наз. наиб, вероятной скоростью. Для молекул H2 при T -273К uB ~1500 м/с. При помощи M. р. можно вычислить ср. значение любой ф-ции от скорости молекул: ср. квадрат скорости 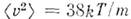 ср. квадратичную скорость
ср. квадратичную скорость 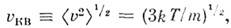 ср. арифметич. скорость
ср. арифметич. скорость 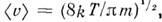 к-рая в
к-рая в 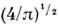 раза больше uB (рис.).
раза больше uB (рис.).M. р. по относит, скоростям молекул и имеет вид
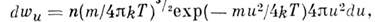
откуда следует, что ср. относит, скорость молекул равна
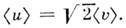
M. р. не зависит от взаимодействия между молекулами и справедливо не только для газов, но и для жидкостей, если для них возможно классич. описание.
В случае многоатомных молекул M. р. имеет место для постунат. движения молекул (для скорости их центра тяжести) и не зависит от внутримолекулярного движения и вращения даже в том случае, когда для них необходимо квантовое описание. M. р. справедливо для броуновского движения частиц, взвешенных в жидкости или газе.
Максвелл использовал для обоснования M. р. детального равновесия принцип.M. р. можно получить из канонического распределения Гиббса для классич. системы, интегрируя по всем пространственным координатам и по всем скоростям, кроме одной, т. к. в классич. случае распределение по скоростям не зависит от распределения по пространственным координатам. M. р. является частным решением кинетического уравнения Больцмана для случая статистич. равновесия в отсутствио впеш. полей. M. р. обращает в нуль интеграл столкновения этого ур-ния, выражающего баланс между прямыми и обратными столкновениями. Во внеш. потенциальном поле имеет место распределение Максвелла - Больцмана (см. Болъцма-на распределение).M. р.- предельный случай Базе- Эйнштейна распределения и Ферми - Дирака распределения в случае, когда можно пренебречь явлением квантового вырождения газа. M. р. подтверждено экспериментально О. Штерном (О. Stern) в 1920 в опытах с молекулярными пучками от источника, помещённого внутри вращающейся цилиндрич. поверхности, и позднее (1947) в опытах И. Эстермана (I. Estermann), О. Симпсона (О. Simpson) и Штерна по свободному падению молекул пучка под действием силы тяжести.
Лит.: Ландау Л. Д., Лифшиц Е. М., Статистическая физика, ч. 1, 3 изд., M., 1976, p 22; Pамзей H., Молекулярные пучки, пер. с англ., M., 1960; Сивухин Д. В., Общий курс физики, 2 изд., т. 2 - Термодинамика и молекулярная физика, M., 1979,
 72-74; Xир К., Статистическая механика, кинетическая теория и стохастические процессы, пер. с англ., M., 1976, гл. 1. Д. H. Зубарев.
72-74; Xир К., Статистическая механика, кинетическая теория и стохастические процессы, пер. с англ., M., 1976, гл. 1. Д. H. Зубарев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.