Akademik

U= RI,(1)

где R - коэф., зависящий от материалапроводника, его геометрии, темп-ры и называемый омическим сопротивлениемили просто сопротивлением. Соотношение (1) описывает участок электрич. цепи в отсутствие источников электродвижущей силы. Чтобы в замкнутойсистеме проводников (электрич. цепи) мог течь стационарный ток, в этойсистеме должны быть участки, где действуют электрич. поля неэлектростатич. происхождения. Эти участки наз. источниками эдс. Если 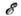- эдс, действующая в неразветвлённой цепи, то вместо (1) имеем

где R - полное сопротивление замкнутойцепи, включающее внутр. сопротивление источника эдс. Это соотношение паз. О. з. для замкнутой цепи. Обобщение (2) на случай разветвлённых цепей см. в ст. Кирхгофа правила. О. з. обобщается на случай переменных (меняющихсяпо гармонич. закону) квазистационарных токов и электрич. цепей, содержащихнаряду с омическим (или, как говорят в таких случаях, активным) сопротивлениемещё и электрич. ёмкости С и индуктивности L. В этом случаеудобно записывать связи между силой тока I и напряжением U вкомплексной форме, понимая под истинными значениями этих величин ReI и ReU соответственно. Введение комплексного сопротивления, или импеданса,

приводит к О. з. для цепи переменного тока:

U= ZI

[напряжение и ток зависят от времени позакону ехр ].Мнимая часть в ф-ле (3) наз. реактивным сопротивлением. Правила Кирхгофаостаются в силе и для цепи, включающей наряду с активным (омическим) иреактивные сопротивления; при этом вместо омических сопротивлений участкацепи следует подставить соответствующий импеданс.
О. з. в дифференциальной форме записываетсяв виде

где коэф. пропорциональности 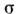наз. электропроводностью. О. з. в интегральной форме может бытьполучен из соотношения (4), если проинтегрировать последнее по объёму рассматриваемогопроводника и учесть, что 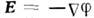и напряжение на участке АВ есть 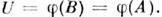Коэф. R и связанысоотношением (для цилипдрич. проводников)

где l - длина проводника,S - площадь его поперечного сечения.
Линейная связь между j и E в проводнике обусловлена линейной зависимостью эфф. силы трения, действующейна носители заряда, от их скорости. Микроскопия, определение плотноститока где е - заряд носителя, v - его скорость (суммирование производитсяпо всем носителям заряда, находящимся в единице объёма проводника). Еслипри движении носителя на него действует сила трения, линейно зависящаяот скорости (как это имеет место при жидком трении), то 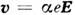и, следовательно,коэф.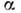наз. подвижностью носителей заряда. Отклонения от О. з. практическивсегда обусловлены изменением плотности и ср. времени свободного пробеганосителей при изменении электрич. поля (полупроводники, газовый разряд).В полуметалле висмуте отклонения от О. з. имеют место при плотностях токавыше, чем (0,5 - 1) х 10¹⁰ А/м ² (Е. С. Боровик, 1953).В металлах отклонений от О. з. не наблюдалось, хотя для ряда металлов (медь, платина, вольфрам) экспериментально проверена область вплоть до (5 - 6)х 10¹⁰ А/м ².
При наличии в проводнике сил неэлектрпч. происхождения, вызывающих ток (т. н. сторонние силы), в (4) под Е следуетпонимать сумму напряжённостей электрич. поля и поля сторонних сил, Е- > Е+ Е ^стор (напр., в случае неоднородного поля темп-рЕ ^стор ~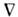 Т).
В анизотропных проводниках (монокристаллы, проводники в магн. поле) направления j и Е в общем случаене совпадают, однако сохраняется линейная связь между компонентами . и Е: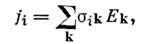

где 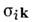- тензор проводимости; i, k= 1, 2, 3.
О. з. (4) записан для неподвижных (относительнонаблюдателя) проводников. Для движущихся со скоростью и (|и|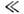с )проводниковвместо (4) следует писать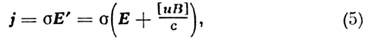

где Е' = Е+ [ иВ]/с - электрич. поло в собств. системе проводника, Е и В -электрич. и магн. поля в системе наблюдателя. Релятивистское обобщение(5) в векторном виде можно записать так:

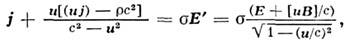
где - плотность заряда в системе наблюдателя,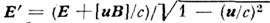

- электрич. поле в собств. системе проводника.
О. з. для плазмы может иметь вид, отличныйот (4) (см. Ома обобщённый закон).

Лит.: Савельев И. В., Курс общейфизики, 2 изд., т. 2, М., 1982; Парселл Э., Электричество и магнетизм, пер. с англ., 3 изд., М., 1983; Сивухин Д. В., Общий курс физики, 2 изд.,[т. 3] - Электричество, М., 1983; А х и е-з е р А. И., А х и е з е р И. А., Электромагнетизм и электромагнитные волны, М., 1985.

А. И. Ахиезер, И. А. Ахиезер,