- ПАРТОНЫ
-
(от лат. pars, род. падеж partis — часть), составляющие адронов, проявляющиеся в процессах с большой передачей четырёхмерного импульса, в частности в глубоко неупругих процессах.В модели П. считается, что адрон участвует в реакциях лишь нек-рой своей частью (партоном), несущей долю x четырёхмерного импульса (4-им-пульса) адрона Р, т. е. Рпартона= xРадрона. В первом приближении П. рассматриваются как точечные ч-цы, испытывающие только упругие соударения. Напр., глубоко неупругое рассеяние эл-на на протоне выглядит след. образом. Эл-н с 4-импульсом р упруго рассеивается на П. с 4-импульсом хР и приобретает 4-импульс р' (рис. 1). Далее рассеянный П. и «пассивный» остаток протона снова превращаются в адроны, образующие две адронные струи. Согласно закону сохранения 4-импульса, импульс рассеянного П. равен q+хР, где q = р-р' — передача 4-импульса от эл-на к протону. Т. к. масса П. равна хМ, где М — масса протона, то (q+xP)2=x2M2c4. Отсюда следует, что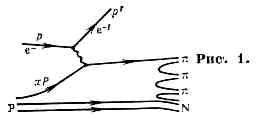 эл-н взаимодействует только с теми П., к-рые несут долю импульса х =-q2/2(Pq). Если число таких П. сорта а обозначить через Fa(x), то сечение глубоко неупругого рассеяния будет равно:ds/dq2dx=SaFa(x)(ds/dq2)a+e®a'+e' (1)где ds/dq2 (благодаря точечности П.) определяется ф-лой Мотта ds/dq2=е2aћ/сq4 (еa — электрич. заряд П. сорта а). Т. о., формфактор глубоко неупругого рассеяния, определяемый как множитель при ф-ле Мотта, оказывается независящим от q2. Это св-во сечения глубоко неупругого рассеяния было названо скейлингом Бьёркена (см. МАСШТАБНАЯ ИНВАРИАНТНОСТЬ).Широкое распространение получила гипотеза, отождествляющая П. с кварками и глюонами. Существует неск. косвенных эксперим. указаний в пользу этой гипотезы, однако прямые доказательства (измерения ср. электрич. и ср. барионного зарядов адронных струй) пока отсутствуют. Комбинируя сечения глубоко неупругого рассеяния в пучках нейтрино и антинейтрино, к-рые взаимодействуют с разными кварками (vm+р®m-+X, v=m+р ® m++ X), можно получить распределения по импульсам всех кварков и антикварков по отдельности (рис. 2). Оказалось, что суммарный импульс всех кварков и антикварков в протоне составляет ок. 50% импульса протона, т. е. половина его импульса связана с нейтральными составляющими, названными глюонами.
эл-н взаимодействует только с теми П., к-рые несут долю импульса х =-q2/2(Pq). Если число таких П. сорта а обозначить через Fa(x), то сечение глубоко неупругого рассеяния будет равно:ds/dq2dx=SaFa(x)(ds/dq2)a+e®a'+e' (1)где ds/dq2 (благодаря точечности П.) определяется ф-лой Мотта ds/dq2=е2aћ/сq4 (еa — электрич. заряд П. сорта а). Т. о., формфактор глубоко неупругого рассеяния, определяемый как множитель при ф-ле Мотта, оказывается независящим от q2. Это св-во сечения глубоко неупругого рассеяния было названо скейлингом Бьёркена (см. МАСШТАБНАЯ ИНВАРИАНТНОСТЬ).Широкое распространение получила гипотеза, отождествляющая П. с кварками и глюонами. Существует неск. косвенных эксперим. указаний в пользу этой гипотезы, однако прямые доказательства (измерения ср. электрич. и ср. барионного зарядов адронных струй) пока отсутствуют. Комбинируя сечения глубоко неупругого рассеяния в пучках нейтрино и антинейтрино, к-рые взаимодействуют с разными кварками (vm+р®m-+X, v=m+р ® m++ X), можно получить распределения по импульсам всех кварков и антикварков по отдельности (рис. 2). Оказалось, что суммарный импульс всех кварков и антикварков в протоне составляет ок. 50% импульса протона, т. е. половина его импульса связана с нейтральными составляющими, названными глюонами.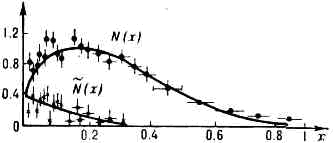 Рис. 2. Распределение кварков N(x) и антикварков N=(x) в протоне.Аналогично в модели П. рассматриваются и др. процессы с большой передачей 4-импульса: рождение в адрон-адронных соударениях пары m+m- с большой относит. энергией, рождение адронов с большим поперечным импульсом и т. д. Сечение каждого из них определяется (подобно (1)) распределением П. в адроне, к-рое не зависит от типа процесса, и сечением партонного подпроцесса, к-рое вычисляется. Это позволяет установить связь между разл. процессами.Партонная модель получила в 70-х гг. обоснование в рамках квант. теории поля. Она оказалась связанной с достаточно быстрым убыванием эффективного заряда при уменьшении расстояния (r): Gэфф(r)С/ln(r0/r), где С и r0 — нек-рые константы. Такое поведение характерно для теорий с размерной константой связи (g)=см-1 (в ед. ћ=1, с=1). Для теорий с логарифмич. убыванием эфф. заряда (асимптотическая свобода в квантовой хромодинамике) в ф-циях распределения остаётся слабая зависимость от q2, нарушающая скейлинг Бьёркена. При этом оказывается, что число «медленных» П. (z-1) с ростом q2 должно возрастать, а число «быстрых» (х=1) — убывать. Подобная тенденция в поведении ф-ций распределения наблюдается экспериментально.
Рис. 2. Распределение кварков N(x) и антикварков N=(x) в протоне.Аналогично в модели П. рассматриваются и др. процессы с большой передачей 4-импульса: рождение в адрон-адронных соударениях пары m+m- с большой относит. энергией, рождение адронов с большим поперечным импульсом и т. д. Сечение каждого из них определяется (подобно (1)) распределением П. в адроне, к-рое не зависит от типа процесса, и сечением партонного подпроцесса, к-рое вычисляется. Это позволяет установить связь между разл. процессами.Партонная модель получила в 70-х гг. обоснование в рамках квант. теории поля. Она оказалась связанной с достаточно быстрым убыванием эффективного заряда при уменьшении расстояния (r): Gэфф(r)С/ln(r0/r), где С и r0 — нек-рые константы. Такое поведение характерно для теорий с размерной константой связи (g)=см-1 (в ед. ћ=1, с=1). Для теорий с логарифмич. убыванием эфф. заряда (асимптотическая свобода в квантовой хромодинамике) в ф-циях распределения остаётся слабая зависимость от q2, нарушающая скейлинг Бьёркена. При этом оказывается, что число «медленных» П. (z-1) с ростом q2 должно возрастать, а число «быстрых» (х=1) — убывать. Подобная тенденция в поведении ф-ций распределения наблюдается экспериментально.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПАРТОНЫ
-
(от лат. pars, род. падежpartis - часть) - общее название составляющих адрона, проявляющихся в процессахс большой передачей импульса (в жёстких процессах), а также в множественныхпроцессах. Модель П. предложена Р. Фейнманом (R. Feynman) в 1969 дляобъяснения различия в характере поведения сечений высокоэнергетич. упругогорассеяния и глубоко неупругого рассеяния электрона на протоне набольшиеуглы: упругий процесс происходит как на протяжённом объекте, а глубоконеупругий - как на точечном. Фейн-ман объяснил это различие, предположив, что протон состоит из точечных частиц - П., к-рые проявляются во взаимодействияхлишь при больших переданных импульсах (т. е. на малых расстояниях). Дальнейшееизучение партонной модели и сопоставление её предсказаний для жёстких процессовс экспериментом позволило отождествить П. с кварками и глюонами, взаимодействие к-рых описывается квантовой хромодинамикой (КХД).Согласно кварковой модели, адрон состоит либо из трёх кварков, либо изкварка и антикварка. В квантовой теории поля из-за эффекта поляризациивакуума каждый кварк (антикварк) окружён облаком глюонов и кварк-антикварковыхпар. Вследствие этого релятивистский адрон в модели П. представляется каккогерентная совокупность бесконечного числа кварков, антикварков и глюонов. При этом разность чисел кварков и антикварков каждого типа (аромата), т. е. число валентных кварков, конечна и определяет аддитивные квантовые числаадрона (электрич. заряд, странность, барионное число и т. д.). Так, протонсодержит два валентных u -кварка, один валентный d -кварк, а также море кварк-антикварковых пар (т. н. морских кварков и антикварков)и глюонов.
Каждый нач. адрон участвует в реакцияхлишь одним, активным. П., несущим (приближённо, с точностью до M2/Q2, где М - масса адрона, а Q2 М 2_ квадрат характерной передачи 4-импульса в жёстком процессе)нек-рую долю х продольного 4-импульса р адрона (используетсясистема единиц, в к-рой с =1). Т. о., 4-импульс k партонаравен: k= хр + k Т, где k Т -поперечная составляющая 4-имнульса П. [(pkT)= 0]. Плотностьчисла П. сорта а в адроне А наз. функцией распределения f а/А( х).Рассеянные, активные, П. и непровзаимодействовавшие "остатки" нач. адронов(совокупность пассивных П., или П.-спектаторов, от англ. spectator - наблюдатель)превращаются в струи адронные, имеющие тот же импульс, ср. электрич. заряд, барионное число и др. сохраняющиеся квантовые числа (за исключением цвета), что и породивший их П. (или остаток адрона). Плотность распределениячисла адронов А в струе по долям z продольной компоненты 4-импульса(относительно 4-импульса исходного партона а )описывается функциейфрагментации DA/а(z).
М 2_ квадрат характерной передачи 4-импульса в жёстком процессе)нек-рую долю х продольного 4-импульса р адрона (используетсясистема единиц, в к-рой с =1). Т. о., 4-импульс k партонаравен: k= хр + k Т, где k Т -поперечная составляющая 4-имнульса П. [(pkT)= 0]. Плотностьчисла П. сорта а в адроне А наз. функцией распределения f а/А( х).Рассеянные, активные, П. и непровзаимодействовавшие "остатки" нач. адронов(совокупность пассивных П., или П.-спектаторов, от англ. spectator - наблюдатель)превращаются в струи адронные, имеющие тот же импульс, ср. электрич. заряд, барионное число и др. сохраняющиеся квантовые числа (за исключением цвета), что и породивший их П. (или остаток адрона). Плотность распределениячисла адронов А в струе по долям z продольной компоненты 4-импульса(относительно 4-импульса исходного партона а )описывается функциейфрагментации DA/а(z).
Напр., глубоко неупругий процесс рассеяния электрона на протоне выглядит в модели П. след. образом. Электрон с4-пмпульсом l упруго рассеивается на П. с 4-импульсом хр иприобретает 4-импульс l' (рис. 1; - виртуальный фотон). Далее рассеянный П. и пассивный остаток протона превращаютсяв две адронные струи, одна из к-рых летит в направлении виртуального фотона, а другая - в направлении первичного протона.
- виртуальный фотон). Далее рассеянный П. и пассивный остаток протона превращаютсяв две адронные струи, одна из к-рых летит в направлении виртуального фотона, а другая - в направлении первичного протона.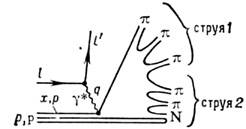
Рис. 1.
Т. к. соударение упругое, то массы начальногои конечного П. равны, т. е. (q+ хр)2= х 2 р 2, где q =l' - l - переданный нартону 4-импульс. Отсюдаследует, что рассеивающийся электрон взаимодействует только с П., несущимдолю х импульса, равную .= Q2/2(pq), где Q2 = - q2. Если fa/p(x)- число таких П. сорта а в протоне р, a ea - зарядпартона а (в единицах элементарного электрич. заряда), то дифференц. сечение глубоко неупругого рассеяния (ГНР) равно:
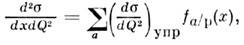
где
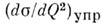 ~
~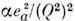 - сечениеупругого рассеяния электрона на точечной частице (
- сечениеупругого рассеяния электрона на точечной частице (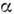 = 1/137 - постоянная тонкой структуры). Т. о., структурныефункции ГНР в модели П., в отличие от формфакторов упругогорассеяния, зависят только от отношения Q2/2pq.
= 1/137 - постоянная тонкой структуры). Т. о., структурныефункции ГНР в модели П., в отличие от формфакторов упругогорассеяния, зависят только от отношения Q2/2pq.
Аналогично ГНР рассматриваются и др. жёсткиепроцессы, напр. рождение пары мюонов с большой относит. энергией в адрон-адронномсоударении, А + В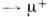 +
+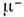 + X,где X - совокупность вторичных адронов (рис. 2, а )или рождениеадрона (С) с большим поперечным относительно оси соударения импульсом, А +В
+ X,где X - совокупность вторичных адронов (рис. 2, а )или рождениеадрона (С) с большим поперечным относительно оси соударения импульсом, А +В 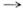 С + X (рис. 2, б; g - глюон). Сечение каждого из них определяетсяф-циями распределения П. в исходных адронах А и В и ф-цией фрагментациирассеянного П. в конечный адрон С, к-рые не зависят от вида процесса, исечениями партонных подпроцессов - аннигиляцией П. и (морского) антипартонав пару
С + X (рис. 2, б; g - глюон). Сечение каждого из них определяетсяф-циями распределения П. в исходных адронах А и В и ф-цией фрагментациирассеянного П. в конечный адрон С, к-рые не зависят от вида процесса, исечениями партонных подпроцессов - аннигиляцией П. и (морского) антипартонав пару 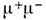 в первом случае и П.-партонным рассеянием - во втором. Т. о., модель П. даёт возможность установить связь между сечениями разл. процессов.
в первом случае и П.-партонным рассеянием - во втором. Т. о., модель П. даёт возможность установить связь между сечениями разл. процессов.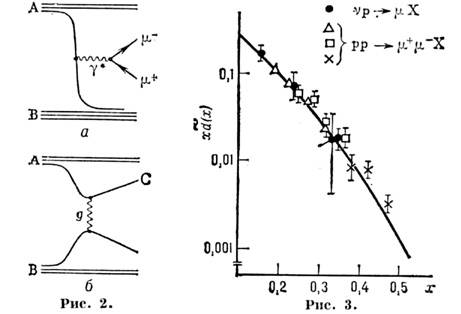
В качестве иллюстрации на рис. 3приведено сравнение распределений антикварков
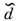 впротоне, полученных из процессов ГНР нейтрино на протоне и рождения пары. Модель П. используется также для феноменологич. описания инклюзивныхсечений рождения мезонов М с малыми поперечными импульсами в областифрагментации и пионизации множественных процессов. В качестве подпроцессовиспользуется реакция слияния кварка (или антикварка) фрагментирующего адронас антикварком (кварком) из моря второго адрона (рис. 4, а )или извакуума (рис. 4, б), а дифференц. сечение пропорц. распределениюкварков в фрагментирующем адроне в первом случае и произведению соответствующихраспределений - во втором. Сам же подпроцесс слияния характеризуется нек-ройфеноменологич. константой.
впротоне, полученных из процессов ГНР нейтрино на протоне и рождения пары. Модель П. используется также для феноменологич. описания инклюзивныхсечений рождения мезонов М с малыми поперечными импульсами в областифрагментации и пионизации множественных процессов. В качестве подпроцессовиспользуется реакция слияния кварка (или антикварка) фрагментирующего адронас антикварком (кварком) из моря второго адрона (рис. 4, а )или извакуума (рис. 4, б), а дифференц. сечение пропорц. распределениюкварков в фрагментирующем адроне в первом случае и произведению соответствующихраспределений - во втором. Сам же подпроцесс слияния характеризуется нек-ройфеноменологич. константой.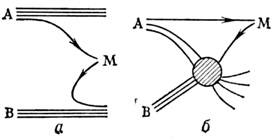
Рис. 4.
Равенство аддитивных зарядов адрона и егоимпульса сумме зарядов и продольных составляющих импульсов П. и аналогичноеравенство для адронов партонной струи приводит для ф-ций распределенияи фрагментации к зарядовым и импульсным правилам сумм:
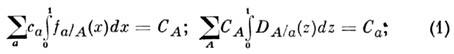
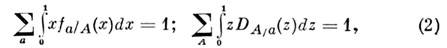
где с а (С А) - величинасохраняющегося заряда (электрич. заряда, барионного числа и др.) партона а (адрона А), а суммирование производится по всем сортамП. и антипартонов (адронов и антиадронов).
Поведение ф-ций распределения кварков-П. в области малых х может быть связано с поведением полных сеченийфотопоглощения виртуального -квантана адроне при большой полной энергии в системе центра инерции
-квантана адроне при большой полной энергии в системе центра инерции  и определяется в Редже полюсов методе обменом реджеоном для валентныхкварков-П. qV, т. е. для комбинации распределений
и определяется в Редже полюсов методе обменом реджеоном для валентныхкварков-П. qV, т. е. для комбинации распределений 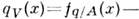
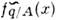 ,и обменом помероном для морских П., т. е. для комбинации O(х)=fq/A(x) - qV(x )(совпадающей с плотностьюраспределения виртуальных пар кварк-антикварк) и глюонов. Вследствие этогоуказанные комбинации ведут себя в пределе х
,и обменом помероном для морских П., т. е. для комбинации O(х)=fq/A(x) - qV(x )(совпадающей с плотностьюраспределения виртуальных пар кварк-антикварк) и глюонов. Вследствие этогоуказанные комбинации ведут себя в пределе х  0соответственно как
0соответственно как 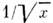 и 1/х. В др. пределе x
и 1/х. В др. пределе x 1 оно связано со степенью убывания формфактора адрона с ростом Q2 и, согласно кваркового счёта правилам (см. также Автомодельная асимптотика), определяется числом n пасс пассивных кварков-П.:
1 оно связано со степенью убывания формфактора адрона с ростом Q2 и, согласно кваркового счёта правилам (см. также Автомодельная асимптотика), определяется числом n пасс пассивных кварков-П.:f(x)~ (1 - x)2nпасс-1.
Напр., для распределения валентных u -кварковв протоне это даёт uV(x)~ (1 - х)3 (п пaсс.2), а для морских кварков и антикварков О(х)~ (1 - х)7 (п пaсс.4). Аналогичные предельные поведения с заменой х на z справедливы и для ф-ций фрагментации.
Наилучшим процессом для эксперим. измерениякварк-партонных распределений является ГНР нейтрино и антинейтрино, к-рыевзаимодействуют с разными кварками: нейтрино с d- и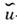 -кварками, антинейтрино с
-кварками, антинейтрино с 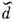 и и. Эти распределения для валентных и -кварков хи V (х )и морских антикварков
и и. Эти распределения для валентных и -кварков хи V (х )и морских антикварков 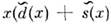 ) в протоне показаны на рис. 5, а. Видно, что импульсный спектрморских кварков мягче спектра валентных кварков; это качественно согласуетсяс использовавшимся ранее представлением о нуклоне, как о состоящем из центр. ядра (керна), окружённого облаком мезонов. На рис. 5( б) показаноотношение распределений dV(x)/uV(x). Сплошные линии -простейшие параметризации этих распределений:
) в протоне показаны на рис. 5, а. Видно, что импульсный спектрморских кварков мягче спектра валентных кварков; это качественно согласуетсяс использовавшимся ранее представлением о нуклоне, как о состоящем из центр. ядра (керна), окружённого облаком мезонов. На рис. 5( б) показаноотношение распределений dV(x)/uV(x). Сплошные линии -простейшие параметризации этих распределений: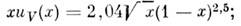
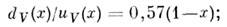
Из этих данных видно, что валентныекварки несут ок. 35% полного импульса протона, морские - ок. 10%. Остальные55% приходятся на долю глюонов. Непосредственно распределение глюонов измеряетсяв процессе рождения тяжёлых кваркониев (например, J/
 -частицы)в ГНР (рис. 6) и имеет вид xg(x)
-частицы)в ГНР (рис. 6) и имеет вид xg(x)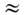 3,3(1-x)5.
3,3(1-x)5.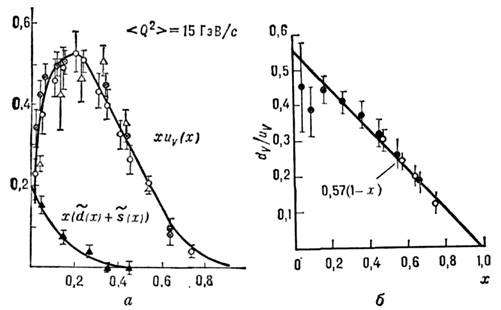
Рис. 5.
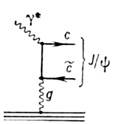
Рис. 6.
Для измерения распределения П. в других(нестабильных) частицах используется процесс рождения мюонных пар (рис.2, а).
Для измерения ф-ций фрагментации наиб. подходящим процессом считается рождение адронных струй в процессе е+е - -аннигиляции.
Модель П. для жёстких процессов получилатеоретич. обоснование и уточнение в КХД, где она является следствием свойствафакторизации сечений жёстких процессов. Уточнения сводятся к слабой (логарифмич.)зависимости ф-ций распределений и фрагментации от Q2, к-раяопределяется ур-ниями эволюции КХД, к учёту убывания константы взаимодействиякварков-П.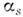 от Q2 и к отходу от точечности П., т. е. к учёту неупругихподпроцессов и радиационных поправок по теории возмущений КХД.
от Q2 и к отходу от точечности П., т. е. к учёту неупругихподпроцессов и радиационных поправок по теории возмущений КХД.
Ур-ния эволюции приводят к росту структурныхф-ций с увеличением Q2 в области малых х, х <0,2,при этом ср. доля импульса валентных кварков уменьшается, а ср. доли импульсаморских кварков и глюонов стремятся к пост. значениям, равным 3nf/(16 + 3nf )и 16/(16 + 3nf),где nf - число ароматов кварков. Суммарная же доля импульсоввсех П. [соотношения (2)] и их суммарные заряды [соотношения (1)] не зависятот Q2. Эти изменения ф-ций распределения и фрагментацииподтверждаются экспериментально.
Т. о., модель П. к кон. 1980-х гг. являетсякак основой приложения КХД к жёстким процессам, так и основой мн. феноменологич. моделей взаимодействия адронов.Лит.: Фейнман Р., Взаимодействиефотонов с адронами, пер. с англ., М., 1975; Клоуз Ф., Кварки и партоны, пер. с англ., М., 1982; Радюшкин А. В., Анализ жестких инклюзивных процессовв квантовой хромодинамике, "ЭЧАЯ", 1083, т. 14, с. 58; Волошин М. Б., Тер- Мартиросян К. А., Теория калибровочных взаимодействий элементарных частиц, М., 1984.
А. В. Ефремов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.