Akademik

Процедура П. должна удовлетворять условию р е н о р м а л и з а ц и о н н о й и н в а р и а н т н о с т и, состоящему в том, что наблюдаемые величины, вычисленные как с помощью первоначальных, так и с помощью новых параметров, должны совпадать.

Поясним это на примере П. электрич. заряда в квант. электродинамике. Величина заряда эл-на определяется через силу, действующую на ч-цу в реальном эл.-магн. поле. Результатом её действия может быть отклонение движущегося эл-на полем к.-л. заряж. источника. Если после вз-ствия полем источника эл-н изменил свой четырёхмерный импульс (4-импульс) l на l', это означает, что, обменявшись с источником виртуальным фотоном, эл-н передал последнему импульс q=l-l'. В КТП такой процесс описывается суммой Фейнмана диаграмм, изображённых на рис. 1 составляющих т. н. вершинную функцию Е(m*), зависящую от массы виртуального фотона m*=??q2?/с и грающую роль эффективного заряда.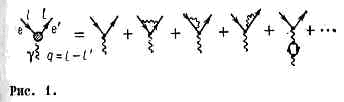

Эта сумма имеет вид ряда по «затравочному» заряду е0 — параметру в исходных ур-ниях теории поля, харакризующему интенсивность вз-ствия,

Е(m*, е0) =e0+(e30/ћc)f1(m*)+... (1)

(где f1 — нек-рая ф-ция от m*), причём первое слагаемое описывает диаграмму а, а второе — сумму остальных диаграмм, изображённых на рис. Величиной же физ. заряда, согласно обычному определению, наз. величина той ф-ции при m*=0 (реальное эл.-магн. поле), т. е.

е=Е(m*=0, е0)=e0+(e30/ћc)f(0)+ . . .

Процедура П. заключается в том, что разложение (1) можно переписать в виде

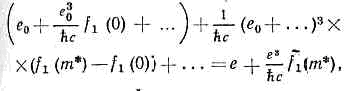т. е. величину физ. заряда е приписать первой диаграмме, а вклады остальных диаграмм переопределить так, чтобы при m*=0 они были бы равны пулю, напр. f=1(m*)=f1(m*)-f1(0); при том, хотя каждое из слагаемых бесконечно велико, их разность f=1 оказывается конечной.

Однако принятый способ определения заряда не единственный. Заряд можно было бы определять и через отклонение эл-на с к.-н. ненулевым квадратом передачи 4-импульса ?q2?=l2с2, где l — нек-рое фиксиров. значение m*?0. Такой новый заряд еl по величине будет отличаться от общепринятого. Эфф. заряд Е(m*, l, еl) будет иметь вид разложения (1), но уже по новому заряду еl, а вклады диаграмм с тремя и большим числом вершин, согласно процедуре П., должны вычитаться в точке m*=l, т. е. Е(m* =l, l, еl)=el. Ренормализац. инвариантность для эфф. заряда означает, что для любой новой точки нормировки m*=l'

Е(m*, l', еl')=Е(m*, l, еl), или, поскольку еl'=Е(l', l, еl), Е(m*, l', Е(l', l, еl))=Е(m*, l, еl).

Это функц. уравнение эквивалентно дифф. ур-нию

m*(dE/dm*)=b(E). (2)

где b — нек-рая ф-ция Е. Ур-ние (2) явл. основным ур-нием ренормализац. группы. Оно говорит о том, что изменение эфф. заряда Е (т*) с изменением передачи 4-импульса полностью определяется ф-цией b(E). Информация об этой ф-ции основывается почти исключительно на теории возмущений.

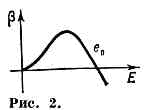В частности, если b(Е)>0 (как, напр., в квант. электродинамике), то эфф. заряд растёт с ростом т* и разложение b(Е) в ряд по Е при достаточно большом Е становится несправедливым. Напротив, если b(Е)0 (как, напр., в квантовой хромодинамике), то с ростом m* эфф. заряд уменьшается и разложение b(Е) становится всё более точным. Это случай т. н. асимптотической свободы. Интересен случай, когда b(E) при нек-ром значении Е=е0 меняет свой знак (рис. 2). Здесь хотя с ростом т* заряд и растёт, скорость этого роста (т. е. b(Е)) уменьшается и при Е=е0 обращается в нуль. Эфф. заряд с уменьшением расстояния (с ростом m*) стремится к конечной величине е0. В этом пределе появляется новое св-во симметрии — масштабная инвариантность: ур-ния теории не изменяются, если все расстояния и времена изменить в одно и то же число раз.