Akademik

- величина, определяющая кол-во электричества dI, протекающего за единицу временичерез произвольно ориентированный элемент поверхности dS:

dI = jdS. П. э. т.

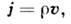
где 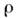- объёмная плотность зарядов, v - скорость движения зарядов. В томслучае, когда имеется неск. сортов заряж. частиц, П. э. т. определяетсякак сумма по всем сортам частиц: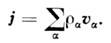

Кол-во электричества, протекающего за единицувремени через всю поверхность, наз. силой тока I:

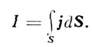
П. э. т. в СИ измеряется в А/м ²(1 А/м ² = 3 x 10⁵ ед. СГС/с см ²). ВекторП. э. т. в общем случае меняется от точки к точке, образуя векторное поле j(r,t). Для геом. изображения векторного поля П. э. т. вводят линиитока. Линии тока определяются так, чтобы касательные к ним в каждой точкесовпадали с направлением вектора П. э. т.
Из закона сохранения электрич. зарядаследует соотношение, к-рому удовлетворяет вектор П. э. т. (ур-ние непрерывности):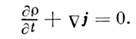

Ур-ние непрерывности можно записать в релятивистски-инвариантномвиде, вводя 4-вектор П. э. т.

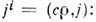
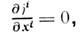
где х ⁱ - координаты четырёхмерногорадиуса-вектора (ct, r). Из ур-ния непрерывности, в частности, следует, что если П. э. т. и плотность заряда не зависят от времени (пост. ток),то линии тока оказываются замкнутыми или уходящими в бесконечность.
На поверхности раздела двух разл. проводящихсред вектор П. э. т. может иметь разрыв. Однако нормальная составляющая j (при условии дr _пов/дt=0, где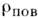 - поверхностная плотность заряда) должна быть непрерывной: j_1n= j_2n
Если проводник граничит с непроводящейсредой, то j _п = 0. Тангенциальная составляющая плотноститока на границе раздела двух проводников с электропроводностям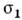и и 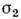удовлетворяетслед. условию: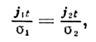

к-рое следует из непрерывности тангенциальнойсоставляющей напряжённости электрич. поля.

Лит.: Тамм И. Е., Основы теорииэлектричества, 10 изд., М., 1989; Ландау Л. Д., Лифшиц Е. М., Теория поля„7 изд., М., 1988. А. В. Тур, В. В. Яновский.