Akademik

БРЕЙТА — ВИГНЕРА ФОРМУЛА

БРЕЙТА — ВИГНЕРА ФОРМУЛА: описывает зависимость эфф. сечения s ядерных реакций от энергии налетающих ч-ц вблизи резонансного значения энергии. Предложена амер. физиками Г. Брейтом (G. Breit) и Ю. Вигнером (Е. Wigner) в 1936. Иногда называется также дисперсионной ф-лой, ввиду сходства с выражением, описывающим дисперсию света. При вз-ствии налетающей ч-цы с ядром-мишенью может образоваться составное ядро С, обладающее рядом квазистационарных уровней энергии. Ширина уровня Г связана со временем жизни т квазистационарного состояния соотношением: Г=h/t. Если энергия (в системе центра инерции) близка к энергии одного из уровней составного ядра, то вероятность образования составного ядра становится особенно большой и сечения резко возрастают, образуя резонансные максимумы. При этом в случае изолированного резонанса (когда Г во много раз меньше расстояния по энергии до других резонансов с теми же квант. числами) а определяется Б.— В. ф. Аналогичная ситуация имеет место при вз-ствии элем. ч-ц, если их полная энергия близка к массе нестабильной элем. частицы — резонанса с соответствующими квант. числами (спином, чётностью, странностью и т. д.).

Б.— В. ф. для сечения реакции a+X®C®b+Y, идущей через составное ядро (или резонанс) С со спином /, вблизи энергии резонанса ?0 имеет вид: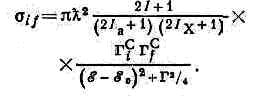

Индексы i и f обозначают входной и выходной каналы; X — длина волны де Бройля, ? — кинетич. энергия ч-ц а и X, Iа, Iх — спины ч-ц и X; Гf и Гi — парциальные ширины уровня составного ядра С, связанные с вероятностью его распада (и образования) по разным каналам f и i. Полная ширина уровня Г=SiГi (рис.).

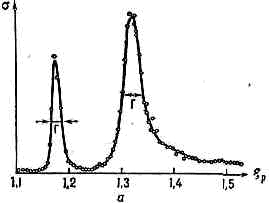Зависимость сечения s реакции 14С (pn)16N (по выходу нейтронов под углом 90°) от энергии протонов ep в лаб. системе координат. Два максимума соответствуют двум уровням составного ядра.

Яд. ширины меняются в зависимости от энергии возбуждения и массы ядра от 0,1 эВ до сотен кэВ. В случае элем. частиц — резонансов ширины лежат в интервале от неск. десятков кэВ до сотен МэВ.