Akademik

ФЕРРИМАГНЕТИЗМ

ФЕРРИМАГНЕТИЗМ: магнитоупорядоченное состояние в-ва, в к-ром магн. моменты атомных носителей магнетизма образуют неск. подрешёток магнитных с магн. моментами Mi, направленными навстречу друг другу или имеющими более сложную пространств. ориентацию; отличная от нуля векторная сумма намагниченностей подрешёток определяет самопроизвольную намагниченность в-ва Js. Обычно подрешётки различаются тем, что содержат ионы иной валентности или ионы другого металла. Простейшая модель ферримагнитной упорядоченности в-ва показана на рис. 1. Ф. устанавливается при темп-рах Т ниже критич. темп-ры Кюри q (см. КЮРИ ТОЧКА). В-ва, в к-рых установился ферримагнитный порядок, наз. ферримагнетиками.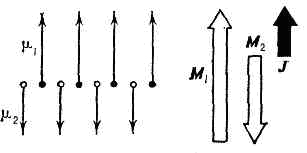

Рис. 1. Схематическое изображение ферримагнитного упорядочения линейной цепочки магн. ионов разных сортов с элементарными магн. моментами m1 и m2. М1 = Nm1 и М2=Nm2— магнитные моменты 1-й и 2-й подрешёток (N — число ионов данного сорта в единице объёма). Суммарная намагниченность J=M1-М2.

Ф. можно рассматривать как наиболее общий случай магн. упорядоченного состояния. С этой точки зрения ферромагнетизм есть частный случай Ф., когда в в-ве имеется только одна подрешётка, антиферромагнетизм — частный случай Ф., когда все подрешётки состоят из одинаковых магн. ионов и Js=0. Термин «ферримагнетизм» был введён франц. физиком Л. Неелем (1948) и происходит от слова феррит — названия большого класса окислов переходных элементов, в к-рых это явление было впервые обнаружено. Часто термином Ф. называют совокупность физ. св-в в-в в указанном выше состоянии.

Магн. подрешётки ферримагнетиков образованы магн. моментами ионов элементов с незаполненной (d- или f-) электронной оболочкой, обладающей собств. магн. моментом. Между ионами разл. подрешёток существует отрицательное обменное взаимодействие, стремящееся установить их магн. моменты антипараллельно. Как правило, это взаимодействие явл. косвенным обменным взаимодействием, при к-ром отсутствует прямое перекрытие волновых функций магн. ионов. Учёт перекрытия волновых функций диамагнитных анионов (F-, O2-, S2-, Se2-) с волновыми функциями магн. катионов переходных металлов (напр., Fe3+ или Mn2+ ) приводит к возможности обменного взаимодействия через виртуальные, возбуждённые состояния. Простейшая схема такого взаимодействия показана на рис. 2. В основном состоянии (a) 2р-оболочка иона кислорода полностью заполнена и, несмотря на перекрытие волновых функций (р-орбиталей O2-и d-орбиталей Fe3+), обменное взаимодействие отсутствует. В возбуждённом состоянии (б) один из р-электронов кислорода переходит на 3d-оболочку иона железа. По правилу Хунда, перейти должен тот электрон, спин к-рого антипараллелен спинам электронов в наполовину заполненной оболочке иона Fe3+ . Оставшийся на 2р-оболочке электрон за счёт отрицательного обменного взаимодействия ориентирует спины электронов соседнего иона железа так, как показано на рис. 2.

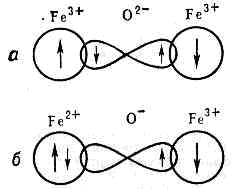Рис. 2. Схема, иллюстрирующая косвенное обменное взаимодействие в системе Fe3+—О2-—Fe3+ : a — основное состояние; б — возбуждённое состояние.

В результате возникает косвенное обменное антиферромагнитное взаимодействие между катионами железа; Изложенная схема относится лишь к одной из возможных моделей косвенного обмена. Существуют и др., более сложные модели. Интенсивность косвенного взаимодействия растёт с увеличением перекрытия электронных оболочек анионов и катионов, т. е. с усилением ковалентной связи. Т. к. ковалентные связи не явл. центрально симметричными, то и косвенное обменное взаимодействие достигает часто макс. значения, когда три взаимодействующих иона не находятся на одной прямой.

При высоких темп-рах, когда энергия теплового движения много больше обменной энергии, в-во обладает парамагн. св-вами (см. ПАРАМАГНЕТИЗМ). Температурная зависимость магнитной восприимчивости парамагнетиков, в к-рых при низких темп-рах возникает Ф., обладает характерными особенностями, показанными на рис. 3. Величина, обратная восприимчивости, у таких в-в следует Кюри — Вейса закону с отрицат. константой q=D при высоких темп-рах, а при понижении темп-ры Т эта величина круто спадает, стремясь к нулю при T®q.

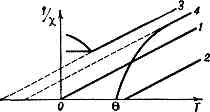Рис. 3. Температурная зависимость величины, обратной магн. восприимчивости, 1/c: 1 — парамагнетика с c=С/Т; 2 — ферромагнетика с c=С/(Т-q); 3 — антиферромагнетика с c=С/(T+q); 4 — ферримагнетика.

В Кюри точке q, когда энергия обменного взаимодействия становится равной энергии теплового движения в в-ве, возникает ферримагн. упорядоченность. В большинстве случаев переход в упорядоченное состояние является фазовым переходом II рода и сопровождается характерными аномалиями темплоёмкости, линейного расширения, гальваномагнитных и др. св-в.

Возникающая ферримагн. упорядоченность атомных магн. моментов описывается определённой магн. структурой, т. е. разбиением кристалла на магн. подрешётки, величиной и направлением векторов намагниченностей подрешёток. Магн. структура может быть определена методами нейтронографии. Образование той или иной магн. структуры зависит от крист. структуры в-ва и соотношения величин обменных взаимодействий между разл. магн. ионами. Обменное взаимодействие определяет только ориентацию векторов намагниченности подрешёток друг относительно друга. Др. их параметр — ориентация относительно осей кристалла — определяется энергией магнитной анизотропии, к-рая на неск. порядков меньше обменной энергии.

Существование в ферримагнетике нескольких разл. подрешёток приводит к более сложной температурной зависимости спонтанной намагниченности J, чем в обычном ферромагнетике. Это связано с тем, что зависимости J(T) для подрешёток могут различаться (рис. 4). В результате самопроизвольная намагниченность, являющаяся в простейшем случае разностью намагниченностей двух подрешёток, с ростом темп-ры от абс. нуля может: 1) убывать монотонно (рис. 4, а), как в обычном ферромагнетике; 2) возрастать при низких темп-рах т в дальнейшем проходить через максимум (рис. 4, б); 3) обращаться в нуль при нек-рой фиксированной темп-ре qк. Темп-ру qк наз. точкой компенсации. При T?qк самопроизвольная намагниченность отлична от нуля.

Впервые теоретич. описание св-в ферримагнетиков было дано Л. Неелем (1948) в рамках теории молекулярного поля. Оказалось, что теория молекулярного поля может объяснить гораздо больше св-в ферримагнетиков, чем металлич. ферромагнетиков (значение величины Js при Т=0, закон Кюри — Вейса при T>q и др.). К ферримагнетикам применима также и теория спиновых волн. В согласии с этой теорией намагниченность многих ферримагнетиков при низких темп-рах следует закону Блоха:

Js=Js0(1-aТ3/2),

где а — константа, Js0— значение Js при Т=0.

Магн. теплоёмкость ферримагнетиков растёт по закону=T3/2.

Ферримагнетики в не очень сильных магн. полях (много меньше обменных) ведут себя так же, как ферромагнетики (см. ФЕРРОМАГНЕТИЗМ), т. к. такие магн. поля не изменяют магн. структуры. В отсутствие поля они разбиваются на домены, имеют характерную намагничивания кривую С насыщением и гистерезисом. В них наблюдается магнитострикция. В ферримагнетиках с неколлинеарными магн. структурами при доступных эксперименту значениях магн. поля насыщение обычно не наблюдается.

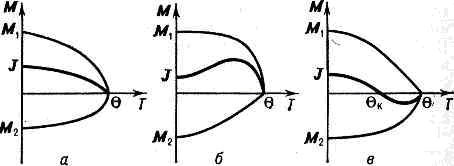Рис. 4. Различные типы температурной зависимости намагниченности подрешёток (M1 и M2) и спонтанной намагниченности (J) для ферримагнетика с двумя магн. подрешётками.

Особыми магн. св-вами ферримагнетики обладают вблизи точки компенсации. В самой точке компенсации магн. св-ва ферримагнетика подобны св-вам антиферромагнетика. В магн. полях, больших поля опрокидывания (для кубич. решётки =1 кЭ), магн. моменты подрешёток устанавливаются перпендикулярно полю и намагничивание происходит путём скашивания подрешёток в направлении поля. В непосредственной окрестности qк поведение ферримагнетика оказывается более сложным. Но и здесь также слабые магн. поля вызывают взаимный скос и опрокидывание подрешёток. Вдали от точки компенсации такие изменения магн. структуры происходят в сильных (порядка обменных) полях.

Огромное большинство ферримагнетиков явл. диэлектриками или полупроводниками. С этим связаны возложности их практич. применения в ВЧ- и СВЧ-устройствах, т. к. в них ничтожно малы потери на вихревые токи в переменных эл.-магн. полях даже очень высокой частоты (см. ФЕРРИМАГНЕТИК, ФЕРРИТЫ).

ФЕРРИМАГНЕТИЗМ

-магнитоупорядоченное состояние вещества, сочетающее свойства ферромагнетизма и антиферромагнетизма; в более общем смысле - совокупность физ. свойств вещества в этом состоянии. Магн. структура в состоянии Ф. определяется взаимной ориентацией векторов намагниченности М_i магнитных подрешё-ток. Самопроизвольная намагниченность М в отсутствие внеш. магн. поля определяется векторной суммой SM_i ; в общем случае в состоянии Ф. 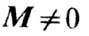Вещества, в к-рых при темп-pax ниже Кюри точки Т _C устанавливается ферри-магн. упорядочение, называют ферримагнетиками (ФМ) (критич. темп-ру называют иногда Нееля точкой T_N). К ним относятся кристаллич. вещества - ферриты, интер-металлич. соединения редкоземельных и переходных металлов, аморфные магнетики того же состава. Простейшая модель ферримагн. упорядочения показана на рис. 1.

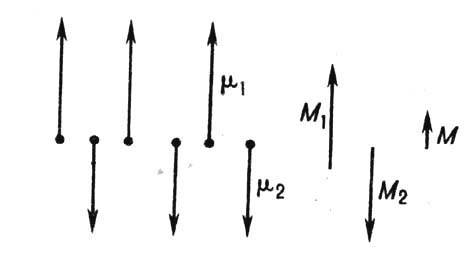
Рис. 1. Схематическое изображение ферримагнитного упорядочения линейной цепочки магнитных ионов различных сортов с магнитными моментами 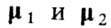N_i- число ионов данного сорта в единице объёма; 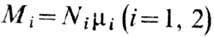-величины намагниченностей подрешёток; суммарная намагниченность M=M₁+M₂, .

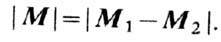Термин "Ф." предложен Л. Неелем (L. Neel) в 1948 при изучении магн. свойств широкого класса магн. окислов - ферритов-шпинелей; им же была разработана феноменоло-гич. теория Ф.

Разл. магн. подрешётки, образующие ФМ, содержат ионы одного и того же элемента с разл. валентностью, ионы разл. металлов или одинаковые ионы с разл. кристалло-графич. окружением. Атомные магн. моменты ФМ создаются электронами незаполненных d- или f -электронных оболочек ионов переходных металлов, входящих в состав ФМ. Между магн. ионами существуют обменные взаимодействия (ОВ) (см. Обменное взаимодействие в м а г н ет и з м е), к-рые, наряду с магнитной анизотропией, определяют магнитную атомную структуру ФМ и обычно носят косвенный характер, при к-ром отсутствует прямое перекрытие волновых ф-ций (см. Косвенное обменное взаимодействие, РККИ-обменное взаимодействие). В ферритах наиб. сильным является ОВ между ионами разл. подрешёток, стремящееся установить магн. моменты подрешёток антипараллельно друг другу.

При высоких темп-pax T>>T_C когда энергия теплового движения много больше обменной энергии, вещество является парамагнетиком. Температурная зависимость обратной магн. восприимчивости ФМ не подчиняется линейному Кюри-Вейса закону, а носит нелинейный (гиперболический) характер (рис. 2). При высоких темп-рах T>>T_C она близка к зависимости для антиферромагнетика, а при 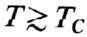- для ферромагнетика. При Т= Т _C обменная энергия становится равной тепловой и в веществе возникает Ф. В большинстве случаев такой переход является магнитным фазовым переходом2-го рода и сопровождается характерными аномалиями физ. свойств.

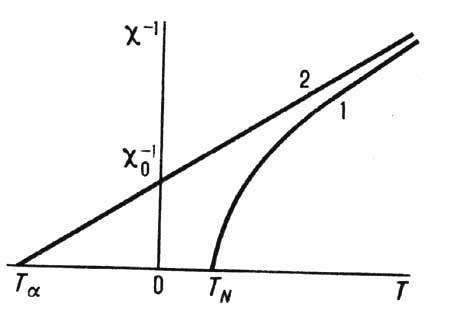
Рис. 2. Температурная зависимость обратной магнитной восприимчивости 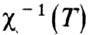(1) и асимптоты 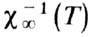(2) двухподрешёгочного ферримагнетика, по Неелю: T_N- точка Нееля; Т _А - асимптотическая точка Кюри.

Магнитная структура ферримагнетиков. Вид магн. упорядочения характеризуется магн. атомной структурой, симметрия к-рой описывается точечными и пространств. группами магнитной симметрии, элементарная магн. ячейка может совпадать с кристаллографической или иметь больший (кратный) период. Наряду с коллинеарными (рис. 1) в ФМ существует большое кол-во сложных неколлинеар-ных и некомпланарных магн. структур. Напр., т р е у г о л ь н ы е структуры (рис. 3) возникают из-за конкуренции внутри- и межподрешёточных ОВ, тогда как з о н т и чн ы е структуры в ферритах-гранатах (рис. 4) возникают благодаря наличию сильной одноионной анизотропии, обусловленной совместным действием спин-орбитального взаимодействия и взаимодействия магн. моментов редкоземельных (РЗМ) ионов с внутрикристаллическим полем.

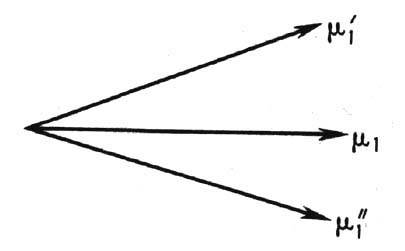
Рис. 3. Схематическое изображение треугольной магнитной структуры одной из подрешёток.

В аморфных ФМ состава R_1-xT_x, где R - Gd, Tb, Dy и др. РЗМ-ионы, а Т - Fe, Co, Ni и др. ионы переходных металлов, магн. ионы занимают случайно размещённые в пространстве позиции с разл. кристаллографич. окружением. Обычно магн. моменты d -ионов упорядочиваются (почти) параллельно друг другу благодаря сильному ОВ, а магн. моменты f -ионов (кроме Gd) заполняют нек-рый конус, результирующая намагниченность к-рого ориентирована антипараллельно намагниченности d -ионов (см. Спери магнетизм). Хотя понятие подрешёток оказывается в данном случае неприменимым, свойства таких магнетиков во многом аналогичны свойствам двухподрешёточ- ных коллинеарных ФМ; имеющиеся отличия обусловлены структурным беспорядком.

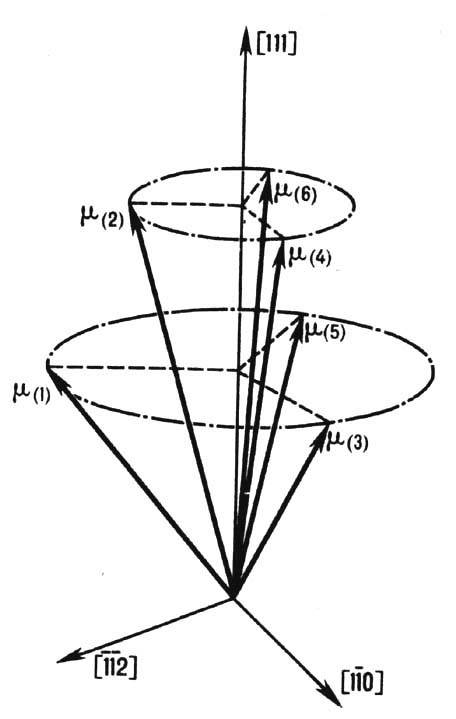
Рис. 4. Зонтичная структура магнитных моментов редкоземельных ионов в ферритах-гранатах. Показаны кристаллографические направления, но- мера в скобках обозначают неэквивалентные кристаллографические позиции.

Прямыми методами определения магн. структуры ФМ является дифракция нейтронов (см. Магнитная нейтронография), а также взаимодействие синхротронного излучения с магн. веществом.

Феноменологическая теория ферримагнетизма. Простейшее описание Ф. даёт теория молекулярного поля, обобщённая на произвольное число магн. подрешёток (т е о р и я Н е е л я). Для изотропного ФМ с двумя неэквивалентными подрешётками 1 и 2 суммарную намагниченность (на грамм-ион) можно записать в виде

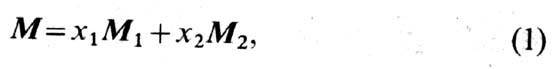
где M₁, M₂ - намагниченности подрешёток (на грамм-ион); х₁, х₂- относит. концентрации ионов в под-решётках (x₁+x₂ = 1).

Молекулярные поля, действующие на ионы, равны соответственно

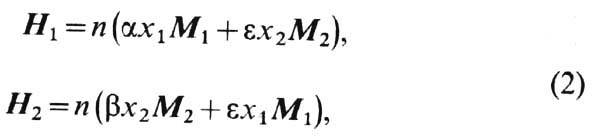
где 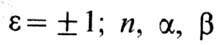-положительные постоянные, связанные с обменными интегралами внутри- и межподрешёточных ОВ. Закон Кюри - Вейса для намагниченностей подрешёток во внеш. поле Н записывается в виде ( С, Т - константа Кюри и темп-pa соответственно)

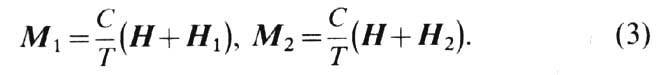
В области темп-р, больших Т _с, обратная магн. восприимчивость подчиняется закону

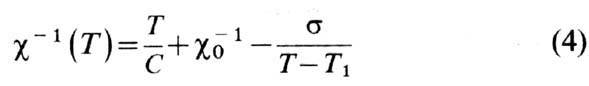
(рис, 2), где постоянные c₀^-1, s, T₁ а также парамагн. точка Кюри Т _C определяются из решения системы ур-ний (1) - (3). В точке Кюри 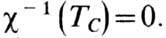При T_C>0 в области темп-р Т<Т _С возникает Ф., при T_C<0 вещество остаётся парамагнитным вплоть до T=0 К. Асимптотика гиперболы определяется ур-нием

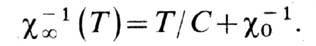
Асимптотич. точка Кюри ФМ на рис. 2 T_A=-Cc₀ Необходимыми условиями возникновения Ф. в рамках теории Нееля являются условия e=-1, ab>1

Ниже Т _C температурная зависимость суммарной намагниченности (1) определяется из решения системы самосогласованных ур-ний для намагниченностей подрешёток М_i, определяемых через ф-ции Бриллюэна с эфф. полями (2).

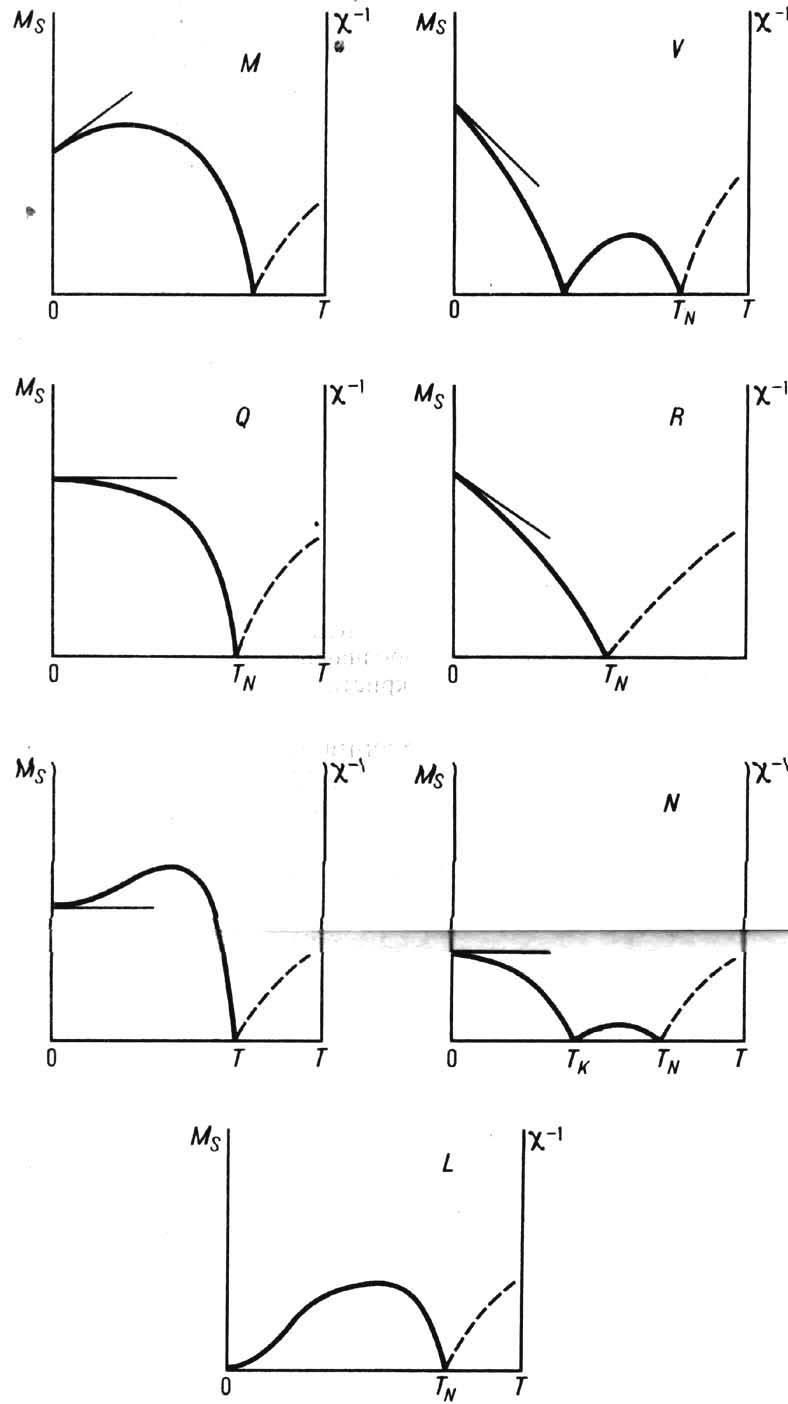
Рис. 5. Основные типы температурной зависимости спонтанной результирующей намагниченности M_s и обратной магнитной восприимчивости c^-1( Т )в двух подрешёточных ферримагнетиках.

Различия в температурных зависимостях М_i, обусловленные наличием внутриподрешёточных ОВ, приводят к разл. видам температурной зависимости результирующей намагниченности (рис. 5). На кривых типа V и N существует т о ч к а м а г н и т н о й к о м п е н с а ц и и T_к, по достижении к-рой намагниченности подрешёток точно компенсируются и результирующая намагниченность равна нулю.

Общее феноменологич. описание Ф. даёт Ландау теория фазовых переходов, основанная на разложении термодина-мич. потенциала системы по степеням параметра порядка (в случае Ф.- по компонентам векторов намагниченностей подрешёток М _i). В рамках этой теории удобно также исследовать ориентационные фазовые переходы в ФМ.

Специфическим свойством для Ф. является поведение ФМ в сильных магн. полях, сравнимых по величине с эфф. полем межподрешёточного ОВ. Простейшая коллинеарная магн. структура (рис. 1) в нек-рых интервалах магн. полей и темп-р может стать неколлинеарной вследствие конкуренции отрицательного ОВ между магн. подрешётками и взаимодействия магн. моментов с внеш. полем Н (С. В. Тябликов, 1957). В малых полях 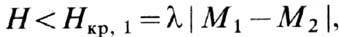где l-константа ОВ между под-решётками, сохраняется нач. состояние ФМ, в сильных полях 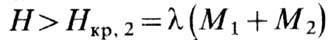вещество находится в индуцированной полем ферромагн. фазе 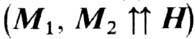, а в промежуточных полях 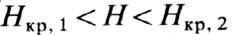возникает неколлине-арная (у г л о в а я) фаза, в к-рой магн. моменты подрешёток составляют разл. углы с направлением поля Н. (Кривая намагничивания изотропного двухподрешёточно-го ФМ изображена на рис. 2 к ст. Ферримагнитный резонанс. )В угловой фазе магн. восприимчивость не зависит от величины поля и равна 1/l Подобное поведение восприимчивости характерно и для антиферромагнетизма.

Наличие вырождения по ориентации магн. моментов относительно внеш. поля в угл. фазе приводит к возможности возникновения доменной структуры в сильных магн. полях (двойникование, тройникование и т. д.); подобные явления наблюдаются также и в сегнетоэлектриках.

Магн. анизотропия существенно изменяет процессы перестройки магн. структуры ФМ и определяет т. н. с п и н-п е р е о р и е н т а ц и о н н ы е ф а з о в ы е п е р е х о-д ы; её влияние особенно важно вблизи точки компенсации Т _к. Магн. фазовая диаграмма двухподрешёточного ФМ с магн. анизотропией 2-го порядка при наложении поля вдоль оси лёгкого намагничивания изображена на рис. 6.

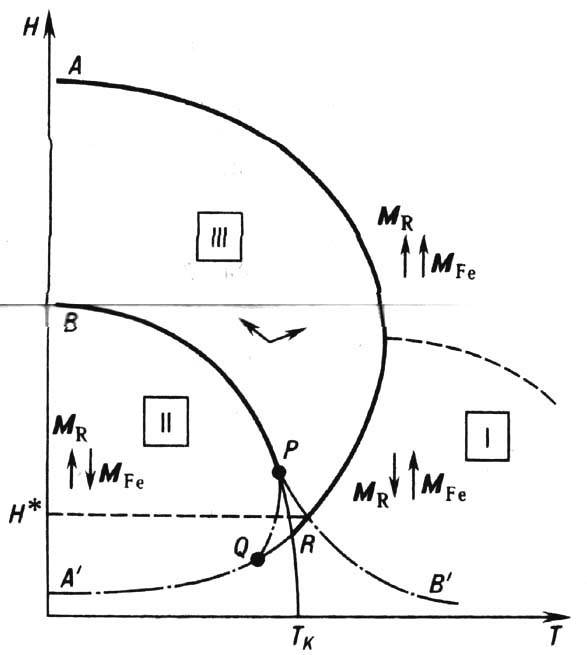
Рис. 6. Магнитная фазовая диаграмма двухподре шёточного ферримагнетика (на примере ферритов- гранатов) при учёте магнитной анизотропии 2-го порядка. Магнитное поле приложено вдоль оси лёгкого намагничивания. Схематически показаны магнитные фазы. Сплошные линии - линии фа зовых переходов (ФП) 2-го рода, тонкая линия- линия ФП 1-го рода, штрих-пунктирные линии- линии потери устойчивости метастабильных фаз.

(Для случая, когда поле приложено вдоль оси трудного намагничивания, см. рис. 3 к ст. Магнитный фазовый переход.) Вдали от Т_к в слабых полях ФМ ведёт себя подобно ферромагнетику, а вблизи Т_к - подобно антиферромагнетику, что приводит к возникновению магн. фазового перехода 1-го рода в угл. фазу. Наличие анизотропии более высоких порядков приводит к ещё более сложному характеру переориентации. На рис. 7 показаны магн. фазовые

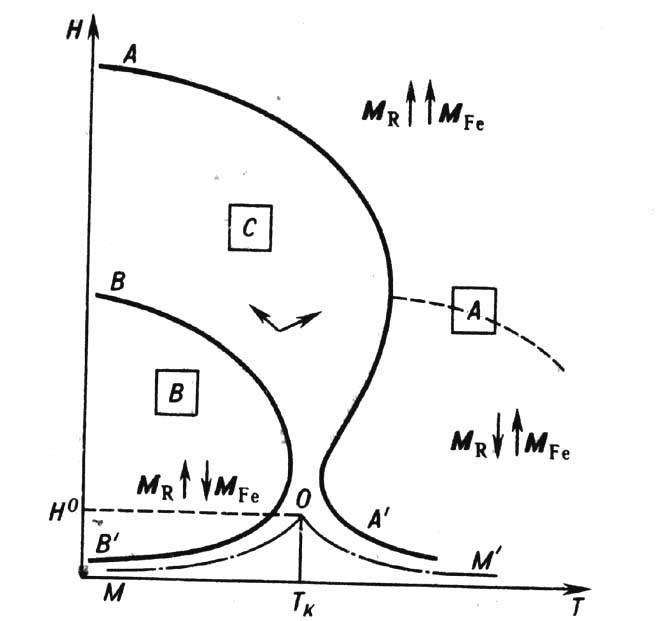
Рис. 7. Магнитная фазовая диаграмма кубических ферримагнетиков для различных ориентации внешнего поля: а) H ||[100]Сплошные линии- линии ФП 2-ю рода; штрих-пунктирная линия -линия ФП 1-го рода между угловыми фазами, О - критическая точка; б) H || [111]

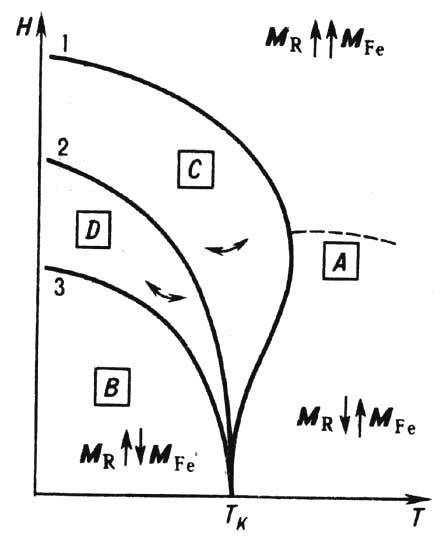
Все линии на диаграмме - линии ФП 1-го рода.

диаграммы ферритов-гранатов при учёте магн. анизотропии 2-го и 4-го порядков с константами K₁, K₂ в случае K₁<0 для ориентации поля вдоль кристаллич. осей [100] и [111]. В первом случае на диаграмме существует трикритическая точка типа наблюдаемой на диаграмме пар-жидкость, а во втором - все фазовые переходы являются переходами 1-го рода. Свойства ФМ, в к-рых энергия магн. анизотропии порядка энергии межподрешёточного ОВ, значительно отличаются от свойств слабоанизотропных ФМ. Переход в индуцированное полем ферромагн. состояние происходит путём одного или неск. фазовых переходов 1-го рода (рис. 8).

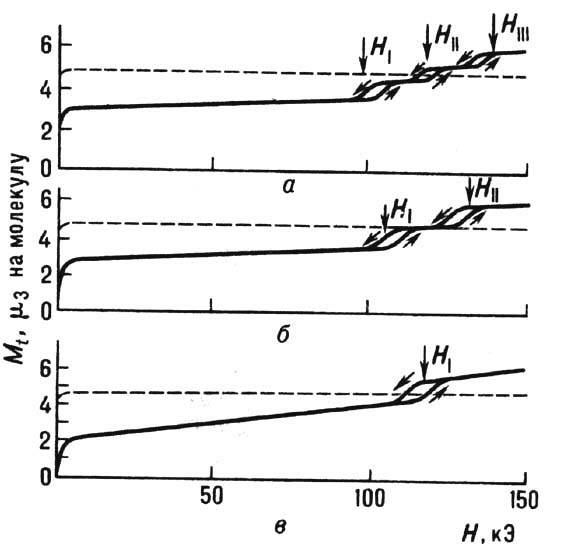
Рис. 8. Кривые намагничивания феррита-граната Y_2,75Hо _o,25Fe₅O₁₂ (сплошные линии); Y₃Fe₅O₁₂ (пунктир) при T=4,2 К для различных направлений внешнего поля: а) H || [111], б) H ||[110], в) H ||[100].

Вблизи Т_к. наблюдается целый ряд аномалий физ. свойств ФМ: значит. рост коэрцитивной силы, температур-ный гистерезис намагниченности, аномалии магнитострик-ции и магнитокалорич. эффекта (рис. 9) и увеличение раз-меров доменов. Константы Верде, Холла и др. подобные характеристики в Т _к не обращаются в нуль, а обнаружива-юг достаточно сложную зависимость от темп-ры и поля что связано с различием соответствующих вкладов, вносимых подрешётками, в силу их разл. кристаллохим. природы.

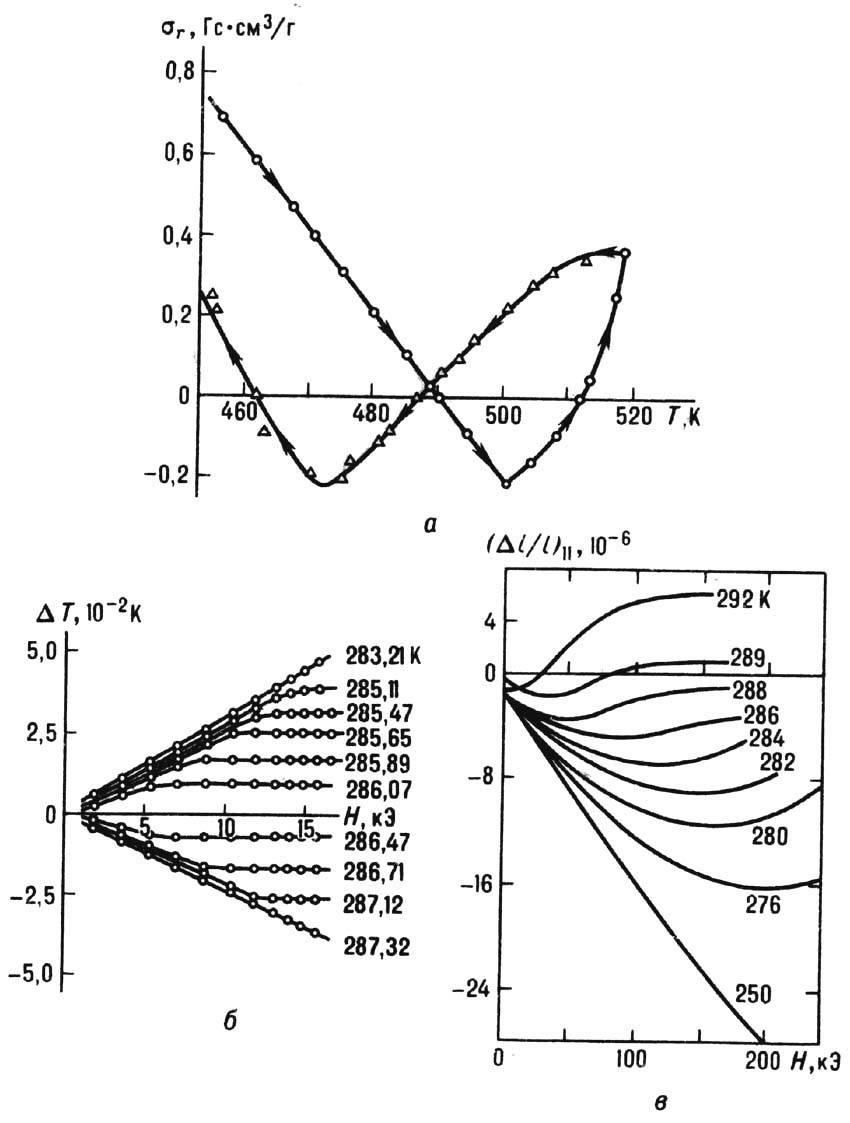
Рис. 9. Аномалии физических свойств ферримагне тиков вблизи точки магнитной компенсации: а- температурный гистерезис намагниченности s_r со единения ErFe₂; б -магнитокалорический эффект в феррите-гранате Gd₃F₅O₁₂; в- продольная магнито стрикция феррита-граната Gd₃F₅O₁₂.

Элементы микроскопической теории ферромагнетизма.

При низких темп-pax классич. теория Ф. становится неприменимой и свойства ФМ описываются квантовой теорией. Для изотропного двухподрешёточного ФМ с подрешётками 1 и 2 гамильтониан может быть записан в виде

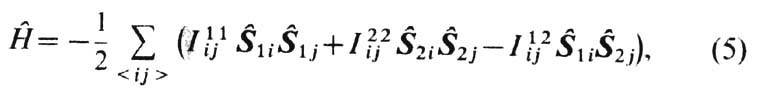
где суммирование проводится по всем магн. ионам i и j; 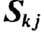- спиновые операторы; символ <...> - означает суммирование по ближайшим соседям; 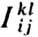-обменные интегралы. Простейшему приближению на основе гамильтониана (5) в случае низких темп-р соответствует теория спиновых волн.

В рамках полуклассич. описания спиновым волнам соответствует прецессия магн. моментов m_ik, ионов, находящихся в узлах кристаллич. решётки r_i, с частотой w и волновым вектором k по закону

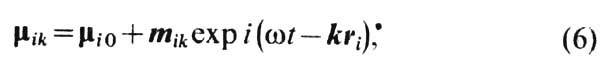
где m_i₀ -ориентация магн. моментов в осн. состоянии (при Т=0К). Определение энергии осн. состояния и закона дисперсии (спектра) спиновых волн, т. е. зависимости w(k), позволяет с помощью методов статистич. физики определить термодинамич. и кинетич. свойства ФМ. Зависимость w(k) можно найти из решения линеаризованных ур-ний Ландау - Лифшица (см. Ферримагнитный резонанс). Общее число ветвей спиновых волн, т. е. разл. типов колебаний, в неогранич. образце равно числу подрешёток п. Для всех ФМ существует одна низкочастотная (акустич.) ветвь, когда векторы намагниченностей ионов движутся согласованно, сохраняя антипараллельную ориентацию, и (n- 1) высокочастотных (оптических, или обменных) ветвей, где антипараллельная ориентация намагниченностей подрешё-ток нарушается.

В квантовой теории спиновые волны представляют собой одночастичные возбуждения (квазичастицы) над осн. состоянием - магноны. Спиновые операторы могут быть представлены с помощью операторов вторичного квантования (обычно бозе-операторов). В наинизшем (квадратичном) порядке после диагонализации с помощью ка-нонич. преобразования (Тябликов, 1948) гамильтониан принимает вид

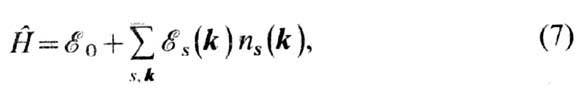
где 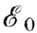-энергия осн. состояния, включающая в себя энергию нулевых колебаний; 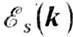-энергия магнона сорта s (соответствующего s-й ветви спектра) с квазиимпульсом k; n_s- число магнонов в данном состоянии. Энергия 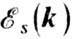определяет в первом приближении собственные частоты нормальных типов связанных колебаний намагниченно-стей подрешёток. В случае изотропного двухподрешёточ-ного ФМ со спинами подрешёгок 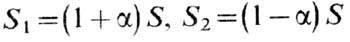(для простоты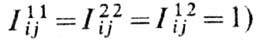

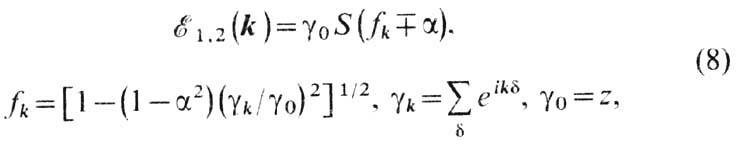
где z - число ближайших соседей; суммирование проводится по первой координац. сфере. Вырождение спектра, характерное для антиферромагн. магнонов (a = 0), отсутствует. В длинноволновом приближении (ka<<1 , где а - постоянная решётки)

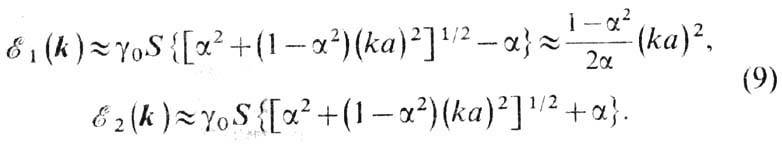
Для низкочастотной ветви имеется область, зависящая от a (т. е. по существу от отношения намагниченностей под-решёток), в к-ром ниж. ветвь квадратична по k, как в ферромагнетиках; при дальнейшем росте k она становится линейной, как в антиферромагнетиках.

Взаимодействие электромагнитного излучения с ферри-магнетиками. Взаимодействие эл.-магн. излучения с ФМ имеет особенности, характерные для магнитоупорядочен-ных веществ, и явл. одним из наиболее широко применяемых инструментов изучения Ф. Увеличение в 10-10³ раз частоты и сигнала ядерного магн. резонанса (ЯМР) связано с увеличением продольной статич. и поперечной ди-намич. составляющих локального поля, действующего на ядерные спины. Измерения частот ЯМР используются для прецизионного определения температурных зависимостей намагниченности подрешёток ФМ. Частоты ЯМР могут различаться не только для разл. ядер, но и для одинаковых ядер с разл. кристаллографич. окружением; методика ЯМР служит одним из косвенных методов определения магн. атомной структуры ФМ.

Ядерный гамма-резонанс (эффект Мёссбауэра) позволяет определить параметры кристаллич. поля, исследовать косвенное обменное взаимодействие. В РЧ-диапазоне наблюдается ферримагн. резонанс.

Многие ФМ являются магнитными диэлектриками или магнитными полупроводниками (напр., ферриты) и прозрачны в видимой области спектра. В нек-рых ферритах-гранатах наблюдаются значит. магнитооптич. эффекты (напр., эффект Фарадея), они также обладают наименьшей диссипацией, при наложении неоднородного статич. поля в них удаётся возбудить бегущие спиновые волны с 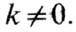Многие работы по эксперим. изучению движения доменных стенок, вертикальных блоховских линий и цилиндрич. магн. доменов проводятся на образцах ферритов-гранатов. ФМ широко применяются как магнитные материалы (см. также Ферриты).

Лит.:Neel L., Magnetic properties of ferrites: ferrimagnetism and antiferromagnetism, "Ann. de Phys.", 1948, v. 3, p. 137; Тябликов С. В., Методы квантовой теории магнетизма, 2 изд., М., 1975; Вонсовекий С. В., Магнетизм, М., 1971; Ориентационные переходы в редкоземельных магнетиках, М., 1979; Хёрд К. М., Многообразие видов магнитного упорядочения в твердых телах, "УФЫ", 1984, т. 142, с. 331; Редкоземельные ионы в магнито-упорядоченных кристаллах, М., 1985; Динамические и кинетические свойства магнетиков, М., 1986; см. также лит. при ст. Ферримаг-нетик, Ферриты. А. К. Звездин, С. Н. Уточкин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.