Akademik

- метод рассмотрения квантовой системы, при к-ром роль независимых переменных играет число частиц в заданном состоянии. В. к. возникло при рассмотрении нерелятивистских систем, состоящих из тождественных частиц. Для бозе-частиц (подчиняющихся статистике Бозе - Эйнштейна) метод В. к. развит в 1927 П. Дираком (P. Dirac, 1927) и в том же году П. Йорданом (P. Jordan) и О. Клейном (О. Klein), для ферми-частиц (подчиняющихся статистике Ферми - Дирака) - Ю. Вигнером (E. Wigner) и Иорданом (1928). Этот метод позволяет рассматривать системы с большим числом степеней свободы и системы с переменным числом частиц. Аппарат В. к. имеет широкое применение в статистич. физике и квантовой теории поля, где рассматриваются процессы с рождением и уничтожением частиц.

В. к. нерелятивистских систем. Рассмотрим квантово-механич. систему из N невзаимодействующих частиц, находящихся во внеш. поле. Пусть 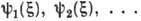- нек-рая полная система одночастичных волновых ф-ций ( 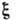включает в себя как пространств. координату 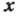, так и спиновую переменную s). Они могут, напр., соответствовать стационарным состояниям одной частицы во внеш. поле. Можно ввести полную систему многочастичных волновых ф-ций след. образом. Пусть N_i - число частиц в состоянии 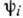. Тогда состояние системы может быть задано набором чисел (N₁, N₂, . . .), указывающим, что N₁ частиц находится в состоянии 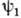, N₂ частиц - в состоянии 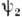и т. д. Вектор состояния системы в этом случае обозначают 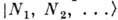. О таком описании системы говорят как об описании в пространстве чисел заполнения или в представлении вторичного квантования.

Для ферми-системы в каждом состоянии может находиться не более одной частицы, N_i=0,1. Для бозе-систем N_i может быть любым неотрицат. целым числом, N_i=0,1, . . ., N. В пространстве чисел заполнения можно рассматривать системы с произвольным числом частиц. Оператор 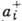, переводящий состояние системы 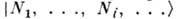в состояние, у к-рого на i -уровне находится N_i+1 частиц,

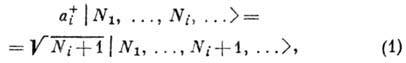
наз. оператором рождения. Оператор, 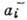, к-рый удаляет частицу с i -уровня,

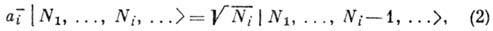
наз. оператором уничтожения. Коэф. 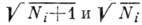в (1) и (2) определяются из условия того, что оператор 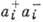является оператором числа частиц в состоянии i, т. е.

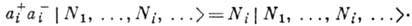
Операторы рождения и уничтожения удовлетворяют перестановочным соотношениям

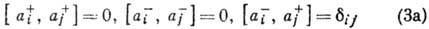
для статистики Бозе - Эйнштейна (квадратные скобки, как обычно, означают коммутатор, т. е. [b, с]=bс-сb )и

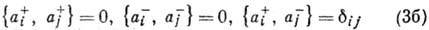
для статистики Ферми - Дирака (фигурные скобки означают антикоммутатор, т. е. 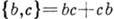; 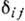- Кронекера символ). Пространство чисел заполнения для бесконечного числа частиц наз. пространством Фока.

Любые квантовомеханич. операторы, заданные, напр., в конфигурационном представлении, можно записать при помощи операторов рождения и уничтожения в представлении В. к. Напр., гамильтониан

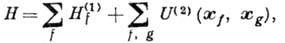
где 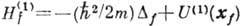- одночастичный гамильтониан, 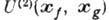- потенциал двухчастичного взаимодействия, в представлении В. к. записывается в виде:

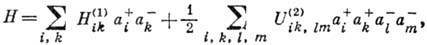
где

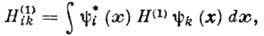
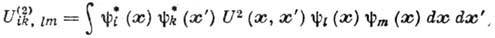
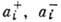- соответственно операторы рождения и уничтожения частиц в состоянии 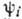одночастичного гамильтониана (без учёта взаимодействия между частицами). Гамильтониан в представлении В. к. может быть записан в более компактной форме, если ввести операторы ,

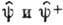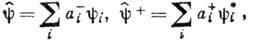
действующие на векторы состояния 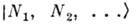в пространстве чисел заполнения:

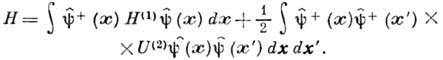
Выражения для операторов 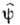аналогичны разложению произвольной волновой ф-ции по полной системе волновых ф-ций 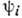. Поскольку, однако, коэффициенты разложения являются не числами, а операторам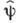и, и 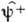наз. вторично квантованными (отсюда назв. метода - "В. к.").

Достоинство метода В. к. в применении к системам взаимодействующих частиц состоит в том, что с его помощью естеств. образом описываются переходы между состояниями системы, вызванные взаимодействием частиц. Эти переходы сводятся к исчезновению частиц в одном состоянии и появлению их в другом. Одновременно аппарат В. к. приспособлен и к рассмотрению процессов с перем. числом частиц - описывает рождение или уничтожение частиц в результате взаимодействия. В квантовой механике всякое слабо возбуждённое состояние системы взаимодействующих частиц может быть представлено как совокупность элементарных возбуждений - квазичастиц. Числа N_i в представлении чисел заполнения в этом случае интерпретируются как числа квазичастиц. Напр., слабо возбуждённое состояние твёрдого тела, обусловленное колебаниями атомов кристаллич. решётки, описывается как совокупность квазичастиц - фононов, свободно движущихся в объёме тела. При этом энергию возбуждения системы можно рассматривать как энергию идеального газа фононов. Осн. состояние системы, в к-ром отсутствуют квазичастицы, можно рассматривать как вакуум, вектор состояния к-рого удовлетворяет условию 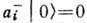. Для слабо взаимодействующего неидеального бозе-газа операторы рождения и уничтожения квазичастиц связаны с операторами рождения и уничтожения исходных частиц Боголюбова каноническими преобразованиями.

Квантование системы гармонических осцилляторов. Рассмотрим важный частный случай - систему га квантовых невзаимодействующих гармонич. осцилляторов (единичной массы) с гамильтонианом

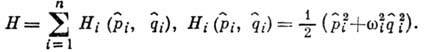
Здесь 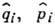- операторы обобщённых координаты и импульса i -осциллятора, а параметры w_i имеют смысл частоты колебаний. Для перехода в представление В. к. вводятся операторы уничтожения и рождения

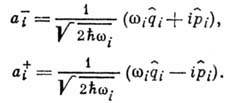
Тогда гамильтониан принимает вид

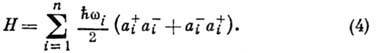
Операторы 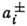удовлетворяют перестановочным соотношениям (3а). Обозначим через 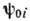решение ур-ния 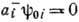; оно интерпретируется как вакуумное состояние i -осциллятора. Введём вакуумное состояние системы п осцилляторов: 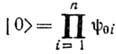. Состояние

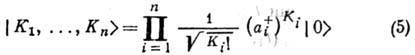
является собств. ф-цией оператора H с собств. значением

;

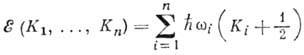оно интерпретируется как состояние, в к-ром имеется K₁ частиц с энергией 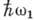, K₂ - с энергией 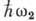и т. д. Векторы состояния (5) при всевозможных значениях Ki (K_i=0, 1, ..., i = l, ..., n) образуют базис в пространстве чисел заполнения. Оператор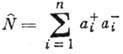

является оператором числа частиц, и

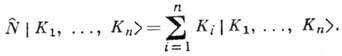
Квантование релятивистских полей. В представлении В. к. можно рассматривать и системы с бесконечным числом степеней свободы - поля физические. Метод В. к. позволяет в этом случае описывать поля как совокупность частиц (квантов. поля).

Рассмотрим классич. свободное скалярное поле 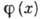, удовлетворяющее Клейна - Гордона уравнению. Ему соответствует лагранжиан

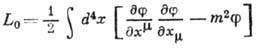
( х - точка пространства-времени, 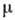=0, 1, 2, 3, постоянная m имеет смысл массы; используется система единиц, в к-рой 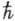=с=1). Соответствующий гамильтониан системы после разложения 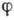по плоским волнам приобретает вид

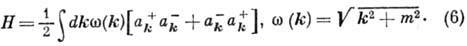
Сравнение ф-л (4) и (6) показывает, что свободное поле можно рассматривать как набор невзаимодействующих осцилляторов в импульсном пространстве (нумеруемых непрерывным трёхмерным индексом k), частота колебаний к-рых зависит от импульса k.

Квантование свободного поля (т. е. сопоставление ему соответствующих частиц) может быть проведено как квантование осцилляторов поля (аналогично квантованию системы гармонич. осцилляторов). Для этого величины 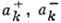в (6) следует рассматривать как операторы, удовлетворяющие перестановочным соотношениям

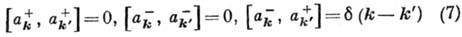
(где 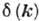- дельта-функция Дирака) и действующие на вектор состояния системы в пространстве чисел заполнения. Процедура квантования свободного поля как совокупности осцилляторов совпадает при условиях (7) с процедурой канонического квантования.

Квантование классич. теории, описываемой набором 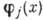классич. полей и лагранжианом L, обычно производится с помощью канонич. квантования (предполагается, что соответствующая классич. система допускает гамильгонову формулировку). При этом на операторы обобщённых координат 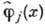и импульсов 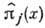накладываются перестановочные соотношения

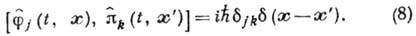
Если построено нек-рое представление перестановочных соотношений (8), такое, что в нём: 1) определено действие оператора Гамильтона H;2) гамильтониан имеет основное (вакуумное) состояние 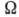; 3) определены средние от полевых операторов в произвольный момент времени t по вакуумному состоянию:

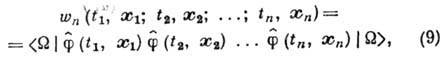
где

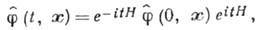
то говорят, что построено квантование полевой системы.

Непосредственно провести описанную выше схему удаётся только для свободных полей. (О квантовании свободного поля Дирака см. Дирака поле. )Для системы свободных полей число сортов частиц и число полей совпадают.

Для лагранжианов вида 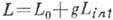, где слагаемое 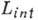описывает взаимодействие полей (g- константа связи), как правило, правая часть (9) может быть построена лишь по теории возмущений по степеням g. При таком построении осуществляется квантование взаимодействующих полей в пространстве Фока, связанном с лагранжианом L₀. Однако включение взаимодействия со сколь угодно малой константой связи g столь существенно меняет картину, что взаимодействующие поля не могут быть определены в фоковском пространстве исходных невзаимодействующих полей. Для преодоления этой трудности разработана процедура устранения расходимостей (см. Квантовая теория поля).

Число полей, из к-рых строится модель, может не совпадать с числом сортов частиц проквантованной системы, аналогично ситуации с квазичастицами в статистич. физике. С одной стороны, могуг появляться связанные состояния, с другой - частиц, соответствующих исходным полям, может не быть. Такая ситуация имеет место в совр. теории сильного взаимодействия - квантовой хромодинамике. Кванты полей, из которых строится модель,- кварки- не наблюдаются, а наблюдаемые адроны являются связанными состояниями кварков.

При квантовании классич. полевой системы полезно иметь информацию о её решениях. Если среди решений классич. ур-ний находятся решения с конечной энергией, локализованной в нек-рой области пространства,- солитоны, то они могут привести к существованию т. н. солитонного сектора в квантовом случае, в к-ром реализованы квантовые солитоны. Квантовые солитоны в принципе могут иметь статистику, противоположную статистике исходных полей. T. о., появляется теоретическая возможность строить фермионы из бозонов. Квантовые солитоны, так же как и связанные состояния, дают возможность, исходя из небольшого числа полей, строить теорию с большим числом наблюдаемых сортов частиц. Одним из практич. методов построения теории в солитонном секторе является квантование системы с помощью фейнмановского функционального интеграла.

Лит.: Бете Г., Квантовая механика, пер. с англ., M., 1965; Боголюбов H. H., Ширков Д. В., Квантовые поля, M., 1980; Дирак П., Принципы квантовой механики, 2 изд., пер. с англ., M., 1979; Ландау Л. Д., Лифшиц В. M., Статистическая физика, ч. 1, 3 изд., M., 1976; Славнов А. А., Фаддеев Л. Д., Введение в квантовую теорию калибровочных полей, M., 1978; Швебер С., Введение в релятивистскую квантовую теорию поля, пер. с англ., M., 1963. Я. Я. Арефьева.