Akademik

- способность плазмы пропускать электрич. ток под действием электрич. поля и сторонних сил (индукц. электрич. поля, градиента давления и др.); физ. величина s, количественно характеризующая это явление. Электрич. ток в плазме представляет собой упорядоченное движение электронной и ионной компонент и определяется величиной зарядов, плотностью частиц, их массой и скоростью движения, а также частотами их столкновений:

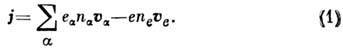
Здесь j - плотность тока,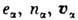- заряд, плотность и ср. скорость ионов сорта 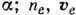- плотность и ср. скорость электронов.

В классич. конденсиров. средах (металлах, электролитах) плотность тока j с большой степенью точности линейно зависит от напряжённости электрич. поля и наводимой эдс ( Ома закон):

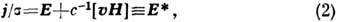
где 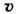- скорость среды, 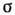- уд. проводимость среды, зависящая от темп-ры.

Простота закона (2) объясняется малой длиной свободного пробега носителей тока. Благодаря этому их движение близко к хаотическому тепловому движению частиц, на к-рое накладывается слабый дрейф вдоль силовых линий электрич. поля 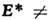0.

В плазме пробеги частиц могут быть самыми разнообразными. При давлении порядка атмосферного в низкотемпературной плазме длина свободного пробега невелика ( 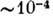см), хотя она и больше пробега в конденсиров. средах. В высокотемпературной плазме длины свободных пробегов частиц очень велики. Так, напр., в токамаках длина свободного пробега 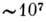см пр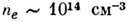и и 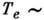10 кэВ. В этих условиях траектории заряж. частиц определяются преим. не столкновениями, а полями, существующими в плазме, и имеют очень сложный вид, а связь j c E* теряет локальный характер (см. Переноса процессы). Такое отличие длины свободного пробега, а следовательно и свойств проводимости высокотемпературной плазмы от низкотемпературной, объясняется тем, что сечение "кулонов-ского" столкновения заряж. частиц быстро падает (а длина свободного пробега растёт) с ростом относит. энергии 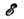сталкивающихся частиц:

Если измерять 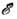в эВ, то 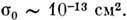Следовательно, при 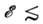1 эВ значение 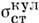существенно больше газокинетического 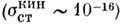, но уже при30 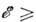эВ оно равно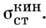

Др. важное отличие плазменных "проводников" от конденсированных заключается в том, что большинство плазменных образований существуют при условии, что через них протекает ток. Таковы классич. электрические разряды в газах, плазма в плазменных ускорителях, тока-маках и др. При изменении тока плазменная структура (конфигурация) плавно или скачкообразно изменяется, в ней могут в широком диапазоне частот развиваться колебания (от акустических до ленгмюровских), на электродах возникать "привязки" и т. п. Около электродов, помещённых в плазму, обычно возникают при-электродные слои, падение потенциала на к-рых может существенно превосходить падение потенциала в осн. части плазменного объёма (напр., в тлеющем разряде). По этой причине для большинства плазменных систем особое значение имеют не дифференциальные, типа (1), а интегральные характеристики П. п. Для стационарных систем это, в первую очередь, вольт-амперные характеристики:

к-рые связывают приложенное напряжение 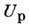с протекающим через плазменную конфигурацию током 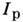В нестационарных условиях их эквивалентами являются "осциллограммы" тока и напряжения: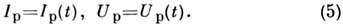

Исключая из этих выражений f, получим для существенно нестационарных разрядов неоднозначные зависимости

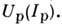
Если длина свободного пробега частиц достаточно мала, то динамику их поведения в плазме можно описать в гидродинамич. приближении (см. Двухжидкост-ная гидродинамика плазмы).

В этом случае для частиц каждого сорта записывается ур-ние движения, учитывающее и давление, и трение компонент друг о друга. Система этих ур-ний предельно упрощена, но тем не менее даёт правильное качественное, а во мн, случаях и количественное описание процессов.

Если время свободного пробега электронов 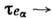0, то усреднённая скорость электронной компоненты оказывается соизмеримой со скоростями тяжёлых компонент, и поэтому, учитывая малую массу электронов, во мн. случаях течение электронной компоненты можно считать безынерционным, а саму её - находящейся в квазистатич. состоянии. В результате ур-ние движения для электронов принимает вид обобщённого закона Ома: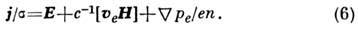

Переход от (6) к (2) сводится к замене 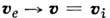и пренебрежению 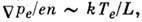где L- характерный масштаб неоднородности плазменного образования. Такой переход означает игнорирование Холла эффекта и термоэлектрич. явлений, и это допустимо для конденсиров. сред, где эти эффекты выражены сравнительно слабо. Однако в плазме они могут стать определяющими. Так, напр., в термоядерных системах 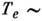10 кэВ, следовательно, термич. разность потенциалов может достигать десятков кВ. В то же время омический член 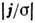может быть очень малым. Так, напр., в токамаке при ср. плотности тока в шнуре

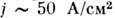и 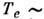10 кэВ П. п.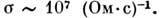

Отсюда 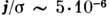В/см. В этих условиях большую роль в плазме начинает играть эффект Холла, т. е. в (6) входит не 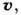как в (2), а 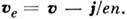Тогда получим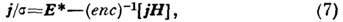

где

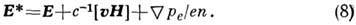
Второй член в правой части (7) обычно наз. холлов-ским. В этом случае различают П. п. по полю и поперёк магн. поля (см. Ома обобщённый закон). Классич. проводимость 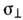поперёк магн. поля с ростом H убывает 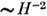, а "холловская" проводимость, обязанная дрейфу электронов в скрещенных E-H -полях, убывает медленнее: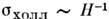. Проводимость вдоль магн. поля от H не зависит. При расчёте тока в плазме по ф-лам (7) и (8) надо знать скорость ионных компонент 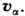В этом случае токи в плазме определяются не просто проводимостью и разностью потенциалов, приложенной к плазменному промежутку, а являются результатом коллективного взаимодействия всей самоорганизующейся плазменной конфигурации. Если конфигурация осесимметрична, а магн. поле имеет только одну азимутальную компоненту 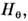то такая конфигурация имеет вид неограниченного цилиндра. Это означает, что если имеется гофриров. проводник, то при 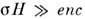линии электрич. тока перестают заходить в выступы (рис. 1).

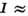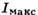Рис. 1. Линии тока в гофрированном проводнике: 1- токовая поверхность, внутри которой 0,9 при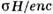

= 5; 2- то же при 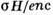= 25.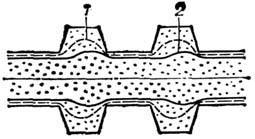

Величина П. п. 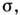введённая феноменологически в гидродинамич. рассмотрении, может быть вычислена более строго [1], с использованием кинетических уравнений для плазмы, тогда для проводимости ионно-элект-ронной плазмы получим ряд ф-л:

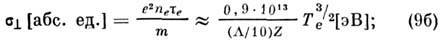
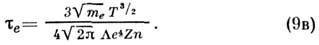
Здесь 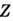- заряд иона, 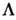- кулоновский логарифм.

В случае полностью ионизованной плазмы проводимость зависит только от темп-ры, возрастая пропорционально 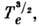и не зависит от концентрации плазмы. Это объясняется тем, что время свободного пробега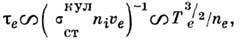

поскольку

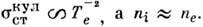
Иначе ведёт себя коэф. электропроводности в случае слабоионизов. плазмы, у к-рой частота столкновений электронов с нейтралами больше, чем с ионами. Его можно определить, зная 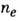и 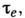по ф-ле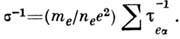

Если плазма достаточно плотная и близка к равновесной, то оценку концентрации электронов можно получить с помощью Саха формулы.

Однако это лишь оценочные расчёты, они могут заметно расходиться с экспериментами из-за загрязнения плазмы. Наличие примесей может существенно увеличивать концентрацию электронов. Учитывая, что при малых энергиях частиц 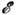кулоновское сечение (3) существенно больше (в 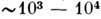раз) газокинетического, газ со степенью ионизации 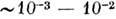может уже рассматриваться как сильноионизованный, а его проводимость определяется по ф-ле (9а).

При достаточно редких столкновениях анализ П. п. требует учёта инерции электронов и кинетич. эффектов, таких, как убегание электронов Будкера - Дрей-сера (см. Убегающие электроны), пристеночная проводимость, аномальное сопротивление, а также проводимость за счёт неоклассич. переноса (см. Переноса процессы).

Благодаря различию скоростей ионной и электронной компонент, приводящему к эффекту Холла, траектории ионов и электронов в плазменных объёмах могут иметь совершенно разный вид (рис. 2). Так, напр., в осесимметричных плазменных ускорителях с замкнутым дрейфом ионы идут вдоль канала в направлении приложенной разности потенциалов, тогда как электроны преим. движутся (дрейфуют) по замкнутым траекториям вдоль азимута, в направлении, перпендикулярном E и Н.

Рис. 2. Схематическое изображение траектории ионов и электронов в плазменном объёме при "сильном" эффекте Холла; сплошные линии - ионы, штриховые - - электроны.

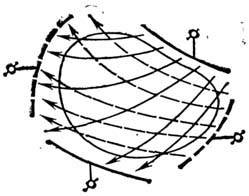
Существ. различие ионных и электронных траекторий приводит к тому, что сопряжение плазменных систем с электродами представляет собой весьма непростую проблему и часто требует сложных многоэлектродных систем, примером к-рых могут служить секцио-ниров. электроды МГД-генераторов. Чтобы уменьшить возникающие здесь трудности, часто стремятся траектории той или иной группы частиц (обычно электронов) сделать замкнутыми.

Лит.:1) Брагинский С. И., Явления переноса в плазме, в сб.: Вопросы теории плазмы, в. 1, М., 1963, с. 183; 2) Райзер Ю. П., Основы современной физики газораз-. рядных процессов, М., 1980. А. И. Морозов.