Akademik

(неоднородная группа Лоренца) - группа всех вещественных преобразований 4-век-торов 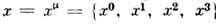пространства Минковского М₄ вида 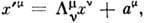где L - преобразование из Лоренца группы, а 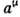- 4-вектор смещения (трансляции). Элемент П. г. обычно обозначается {a, L}, а закон композиции имеет вид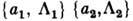

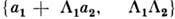= П. г. играет чрезвычайно важную роль в релятивистской физике, являясь группой её глобальной симметрии. Она была введена в 1905 А. Пуанкаре (Н. Poincare). Как и группа Лоренца, П. г. 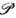имеет четыре компоненты связности, различаемые значениями 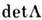и знаком, 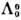а именно: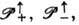 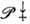и 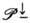. Это - неабелева, некомпактная группа Ли. Наиб. важной является компонента 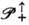, представляющая собой множество преобразований 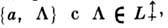содержащая единичное преобразование. В дальнейшем речь будет идти именно об этой группе.

Группа 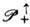- 10-параметрическая; к шести генераторам 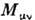группы Лоренца добавляются четыре генератора 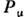трансляций. Ли алгебра П. г. определяется перестановочными соотношениями для генераторов: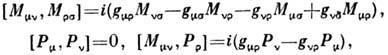

где 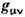- метрич. тензор. 10 генераторов П. г. являются осн. динамич. величинами в релятивистской механике. Величину 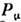наз. вектором энергии-импульса или 4-импульсом; 3-вектор 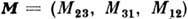есть угл. момент. В квантовой теории поля для любого оператора А (х)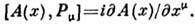

В частности, эволюция во времени определяется оператором P₀, или гамильтонианом системы.

Для П. г. имеется два Казимира оператора, коммутирующих со всеми её генераторами и, следовательно, релятивистски инвариантных. Это 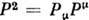p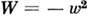, где псевдовектор 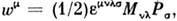а 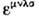- полностью антисимметричный тензор.

При 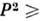0 имеется ещё одна дискретная инвариантная характеристика - знак энергии: 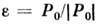с собств. значениями b1.

Как и в случае группы Лоренца, представления П. г. строят с помощью односвязной группы 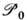- универсальной накрывающей для группы 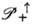(см. Группа). Для квантовой теории поля важны унитарные неприводимые представления 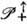(см. Представление группы). Согласно требованию релятивистской инвариантности, векторам состояния отвечают т. н. проективные представления, задаваемые с точностью до фазового множителя. Имеет место теорема Вигнера - Баргмана, утверждающая, что любое проективное представление группы , 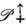порождается обычным однозначным унитарным представлением группы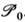

Изучение важных для физики унитарных представлений группы 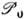сводится к классификации её неприводимых унитарных представлений, т. к. хотя 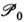и некомпактна, любое её унитарное представление может быть разложено в прямую сумму (или интеграл) неприводимых представлений.

Группа 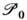локально изоморфна группе 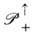и имеет те же генераторы и те же операторы Казимира, что и 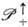. В зависимости от значений оператора P² представления группы 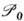могут быть разделены на следующие классы:

1) Р²= m² > 0.

1а) e = 1 (т. е. Р₀ > 0). Соответствующие представления описывают трансформац. свойства реальных частиц с массой покоя т.

1б) e = -1 (т. е. Р₀ < 0). Эти представления комплексно сопряжены с представлениями класса 1а.

2) Р ² = 0, P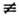0.

2а) e=1 ( Р₀ >0). Соответствующие представления описывают частицы с нулевой массой покоя (нейтрино и фотон).

2б) e = -1 ( Р₀ < 0). Представления этого класса комплексно сопряжены с представлениями класса 2а.

3) Р² =-m² <0 (т. е. вектор P пространственно подобен). Согласно осн. принципам релятивистской механики, частицы с таким импульсом не могут реально существовать. Однако представления класса 3 также встречаются в квантовой теории поля, напр. при описании трансформац. свойств взаимодействующих полей.

4) P= 0. Все состояния с таким P трансляционно инвариантны. Все унитарные представления этого класса, кроме единичного, бесконечномерны. Единичное представление соответствует вакууму, инвариантному относительно всех преобразований из П. г.

Физ. смысл инварианта 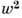выявляется просто при т ²> 0, Р₀ >0. В этом случае величина 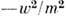равна квадрату угл. момента М² в состоянии покоя, т. е. квадрату спина.

Т. о., неприводимое унитарное представление П. г. характеризуется значениями массы т, спина S изнака энергии (при m² > 0).

Лит.: Боголюбов Н. Н., Логунов А. А., Tодоров И. Т., Основы аксиоматического подхода в квантовой теории поля, М., 1969; Новожилов Ю. В., Введение в теорию элементарных частиц, М., 1972; Мишель Л., Шааф М., Симметрия в квантовой физике, пер. с англ., М., 1974; Ба-рут А., Рончка Р., Теория представлений групп и ее приложения, пер. с англ., т. 1-2, М., 1980; Эллиот Дж., Добер П., Симметрия в физике, пер. с англ., т. 1-2, М., 1983.

С. И. Азаков.