Akademik

- абстрактный объект Т, имеющий определ. систему компонент в каждой рассматриваемой системе координат, такой, что при преобразовании координат его компоненты преобразуются по вполне определ. закону. Каждая точка x n -мерного пространства задаётся в выбранной системе координат набором n чисел ( х ¹, х ², ..., х ⁿ). Переход от одной системы координат к другой означает преобразование (x¹, ..., х ^п) -> ( х'¹, ..., х' ⁿ). Будем рассматривать преобразования, обладающие след. свойствами: 1) 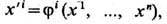i=1, ..., и, где jⁱ -непрерывно дифференцируемые ф-ции, 2) якобиан преобразования, det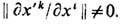

Простейшими примерами Т. являются с к а л я р, к-рый не меняет своего значения при переходе от одной системы координат к другой, и в е к т о р ( а), характеризующийся в данной системе координат и компонентами а'² , ..., а'ⁿ, связанными с компонентами в первоначальной системе координат след. образом:

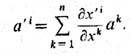
Пусть 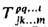-одна из набора ф-ций от переменных x¹, ..., х ⁿ (число верх, индексов равно r, а число ниж. индексов равно s). Эти n^r+s величин являются компонентами Т, ранга (порядка, валентности) r+s при условии, что его компоненты в др. системе координат, х'¹, .,,, х'², даются след. ф-лой:

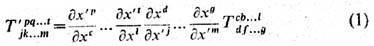
(все индексы принимают значения от 1 до п). Здесь и далее предполагается, что по встречающимся дважды (один раз внизу и один раз вверху) индексам производится суммирование от 1 до n, причём в производных вида дA/дx^k индекс k считается нижним. Такой Т. наз. к о н т р а в а р и а н т-н ы м ранга r и к о в а р и а н т н ы м ранга 5. Верх. индексы являются контравариантными индексами, а нижние - ко-вариантными. Если Т. имеет только контравариантные (верх.) индексы, он наз. контравариантным; если он имеет только ковариантные (ниж.) индексы, он наз, ковариант-ным. Т., имеющий и контравариантные и ковариантные индексы, наз. сметанным. Из (I) видно, что при переходе от одной системы координат к другой компоненты Т. преобразуются линейно и однородно. Если областью определения описанного выше объекта является только одна точка в каждой системе координат, то его обычно наз. просто Т. Если же его область определения - нек-рая область h-мерного пространства, то его наз. т е н з о р н ы м п о л е м. Теория, изучающая тензорные поля, наз. тензорным анализом,

Говорить о том, что нек-рая физ. величина является Т. того или иного ранга, можно только, имея в виду определ. группу преобразований координат в пространстве, в к-ром эта величина рассматривается. При этом если величину можно считать Т. относительно нек-рой группы преобразований, то она является Т, и относительно любой подгруппы этой группы.

Т. о., Т, ранга 0, т. е. Т., имеющий только одну компоненту с одним и тем же значением во всех координатных системах, является скаляром. Примеры скаляров в физике- масса, темп-pa, заряд, кривизна пространства. Т. ранга 1 является вектором. Примеры векторов в трёхмерном пространстве - скорость, импульс, сила, напряжённости электрич. и магн. полей. Нек-рые Т. ранга 2 также имеют спец. названия в геометрии и в физике: напр., метрический тензор в теории римановых пространств и в теории относительности, Т. напряжений (см. Напряжение механическое )и Т. деформаций в механике сплошной среды, Т. диэлектрической проницаемости в электродинамике сплошной среды, тензор энергии-импульса в теории относительности, Т. электромагнитного поля в электродинамике.

Действия над тензорами. Так как Т. задаются своими компонентами в разл. системах координат, то действия над Т. определяются ф-лами, связывающими в каждой системе координат компоненты результата действия через компоненты Т., над к-рыми производятся действия. Алгеб-раич. действия над Т. являются обобщением соответствующих действий над векторами и матрицами.

а) Сложение и вычитание Т. С у м м о й двух Т. А и В с компонентами 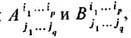имеющих одно и то же строение, т. е. одно и то же число контравариантных и ковариантных индексов, наз. Т. S с компонентами

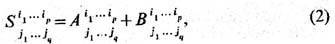
а их разностью - Т. D с компонентами

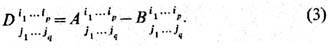
б) Свёртывание смешанного Т. С в ё р т ы в а н и е м сме- шанного Т. наз, операция приравнивания одного контрава- риантного индекса нек-рому ковариантному индексу с по- следующим суммированием по этому индексу. В резуль- тате одного свёртывания ранг Т. уменьшается на два. Если число контравариантных индексов совпадает с числом ко- вариантных индексов, то при полном свёртывании по всем индексам получается инвариант (скаляр).

в) Умножение Т. Произведением (в н е ш н и м п р о и зв е д е н и е м) двух Т. А и В с компонентами 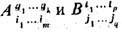(быть может разл. строения) наз. Т. С = АВ с компонентами

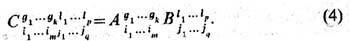
Произведение Т. ассоциативно и дистрибутивно относительно сложения, но, вообще говоря, некоммутативно, т. к. порядок следования индексов в ф-ле (4) является существенным.

В н у т р е н н и м п р о и з в е д е н и е м двух Т. А и В наз. Т., получаемый путём свёртки тензора С[ф-ла. (4)] по. одному или неск. индексам. В общем случае можно образовать неск. таких внутренних произведений.

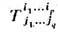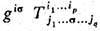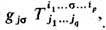Т. наз. а с с о ц и и р о в а н н ы м с т е н з о р о м , если он может быть получен из него подниманием или опусканием нек-рого числа индексов при. помощи внутр. произведений вида или где 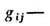ф у н д а м е н т а л ь н ы й м е т р и ч е с к и й Т.,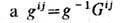 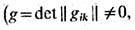G^ik = G^ki - алгебраич. дополнение g_ik в определителе g). Т., ранг к-рого больше единицы, имеет неск. различных ассоциированных Т.

Т., полученные из данного Т. в результате перестановки каких-нибудь верх. (либо ниж.) индексов, наз. изомерами данного Т. Множество изомеров Т. А всегда содержит А. Для всякого Т. контравариантного порядка r и ковари-антного порядка s можно получить r!s!изомеров, но, вообще говоря, не все эти Т. будут различными. Если множество изомеров Т. содержит единственный Т. А, то А наз. симметричным Т.

При рассмотрении прямоугольных координат можно не различать ковариантные и контравариантные индексы, т. к. в этом случае метрич. Т. g_ik имеет наиб. простой вид (единичная матрица).

Признак тензора. Для того чтобы объект X был Т., необходимо и достаточно, чтобы для каждого Т. А нек-рого определённого фиксированного ранга и типа внешнее произведение ХА или какое-нибудь внутреннее произведение объекта X и А было Т. определённого фиксированного ранга и типа.

Лит.: Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; Кильчевский H. А., Элементы тензорного исчисления и его приложения к механике, М., 1954; Схо-утен Я.-А,, Тензорный анализ для физиков, пер. с англ., М., 1965; Сокольников И., Тензорный анализ. Теория и применения в геометрии и в механике сплошных сред, пер. с англ., М., 1971; Векуа И. H., Основы тензорного анализа и теории ковариантов, М., 1978. С. И. Азаков.