Akademik

частица - античастица - один из видов взаимопревращенияэлементарных частиц, в к-ром в результате эл.-магн. или к.-л. др. взаимодействияодновременно возникают частица и античастица. Возможность Р. п. (как и аннигиляция пар)предсказывалась как следствие релятивистского Дирака уравнения. В1933 И. и Ф. Жолио-Кюри (I. et F. Joliot-Curie) с помощью камеры Вильсона, помещённой в магн. поле, наблюдали рождение электрон-позитронных пар -квантамиот радиоакт. источника.

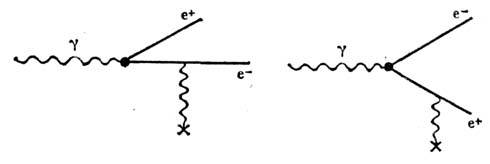
Согласно законам сохранения энергии-импульса, Р. п. одиночным фотономневозможно. Процессы Р. п. фотоном в кулоновском поле (на рис. помеченокрестиком) ядра и атомных электронов при энергии фотона 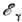, превышающей удвоенную энергию покоя электрона, и при 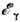,большей 10-30 МэВ (в зависимости от вещества), являются гл. механизмомпотери энергии 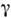-квантовпри их прохождении через вещество (см. Гамма-излучение). Возможентакже процесс Р. п. виртуальным фотоном 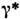(см. Виртуальные частицы), образованным в процессе столкновенияили распада частиц. Такой механизм Р. п. наз. также конверсией фотона. Если энергия фотона (реального или виртуального) очень велика, то он можетпородить любую пару частица - античастица, напр. мюонов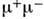

Если при эл.-магн. переходе в ядре образование реального фотона запрещенозаконом сохранения полного момента, то такой переход происходит толькоза счёт процесса конверсии внутренней 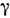-квантаили (при достаточно большой энергии) за счёт конверсии 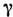-квантав электрон-позитронную пару (парная конверсия).

В столкновениях частиц высоких энергий наблюдается также рождение мюонныхпар. В адронных столкновениях Р. п.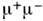связывают с эл.-магн. аннигиляцией кварков и антпкварков, входящихв состав адроное, или с процессами конверсии фотонов тормозногоизлучения, образованных при столкновениях кварков с кварками или глюонами. Поэтомупроцессы Р. п.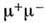и е ⁺ е ^- с большими поперечными (по отношению к осисоударения) импульсами анализируют в рамках квантовой хромодинамики икварк-партонной модели (см. Партоны). В Р. п.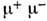смалыми поперечными импульсами важную роль могут играть эл.-магн. распадыадронов (напр.,,).

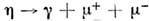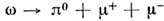Изучение процессов Р. п. (конверсии) в эл.-магн. распадах адронов позволяетполучить информацию об эл.-магн. формфакторах адронов. ПроцессыР. п. новых тяжёлых частиц- с- и b -кварков или тау-лептонов иих последующие лептонные распады являются источником пар т. н. прямых лептоновв адронных столкновениях.

В общем случае любой процесс образования пары частиц с противоположнымилептонными или барионными зарядами можно рассматривать как процесс Р. п. лептонов или кварков, напр.,

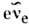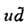
Лит.: Т и н г С., Открытие j-частицы, пер. с англ., «УФН», 1978,т. 125, в. 2, с. 227.

R-ОПЕРАЦИЯ в квантовой теории поля - матем. процедура, применяемаяк коэффициентным ф-циям (см. Операторное разложение, Производящий функционал )матричныхэлементов матрицы рассеяния с целью устранения из них ультрафиолетовыхрасходимостей.

В простых случаях процедуру перенормировок удобно и нагляднопроводить с помощью контрчленов. Однако для коэффициентных ф-цийвысших порядков, отвечающих Фейнмана диаграммам сложной топологии, напр. содержащим т. н. перекрывающиеся расходимости, операция вычитаниярасходимостей требует чёткой и однозначной формулировки. Такая формализацияв импульсном представлении была получена в сер. 1950-х гг. Н. Н. Боголюбовыми О. С. Парасюком в виде теоремы о перенормировках (см. Боголюбова -Парасюка теорема). Рецептурная часть этой теоремы, известная под назв.R-0.Боголюбова, устанавливает относительно простое правило получения конечного, т. е. не содержащего УФ-расходимостей, выражения для коэффициентной ф-ции Т, соответствующей произвольной диаграмме G (обобщённому узлу)данного порядка теории возмущений.

Теорема о перенормировках утверждает, что конечная коэффициентная ф-ция 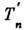,отвечающая данной связной диаграмме n-го порядка G, может быть полученаиз первонач. выражения 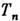применением операции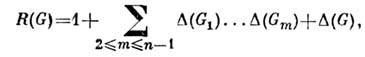

причём сумма берётся по всем возможным разбиениям совокупности элементарныхвершин 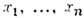(и соединяющих их линий) диаграммы G на поддиаграммы (обобщённыеузлы) С _j:

(* - топологич. произведение). Операция 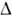определяется следующим образом: для несвязных и слабосвязных (т. н. одночастичноприводимых) диаграмм, а также сходящихся диаграмм 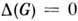. Если к.-л. из поддиаграмм 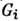совпадает с элементарной вершиной x_i, то 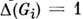.Для слабосвязных расходящихся диаграмм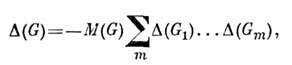

где символ М отвечает операции вычитания из исходного выражения f(k )его w(G) + 1 первых членов разложения в ряд Лорана (или Тейлора)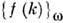по внешней импульсной переменной k: 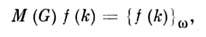причём степень ряда со (G) равна степени расходимости импульсного фейнмановскогоинтеграла, отвечающего диаграмме G.

Для иллюстрации рассмотрим диаграмму 4-го порядка (рис.), описывающуюодин из двухпетлевых вкладов

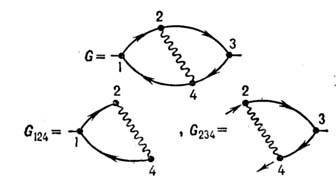
в поляризацию вакуума в квантовой электродинамике. Эта диаграмма 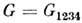содержит две логарифмически расходящиеся поддиаграммы G₁₂₄ иG₂₃₄, так что 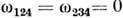. Диаграмма G в целом расходится квадратично w(G) = 2. Поэтому в данномслучае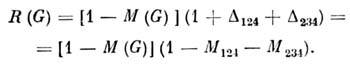

Операторы М₁₂₄ и М ₂₃₄ вычитают логарифмич. расходимости поддиаграмм С ₁₂₄ и С ₂₃₄. Оператор М(G )вычитает квадратичную расходимость диаграммы G в целом.

Как видно, при формулировке R-0. используются в основном топологич. понятия, а устранение расходимостей выполняется путём вычитания из первонач. формального выражения конечных отрезков рядов Тейлора по внешним импульснымпеременным. Поэтому R-0. можно рассматривать как операцию вычитания расходимостей, к-рую можно реализовать без использования вспомогат. регуляризации и употребленияконтрчленов. Такой взгляд отвечает подходу к УФ-расходимостям, основанномуна переопределении произведения пропагаторов, рассматриваемых как обобщённыеф-ции в окрестности световых конусов.

Лит.: Боголюбов Н. Н., Ш и р к о в Д. В., Введение в теорию квантованныхполей, 4 изд., М., 1984, § 29, 30; 3 а в ь я-л о в О. И., Перенормированныедиаграммы Фейнмана, М., 1979, гл. 2. Д. В. Ширков.