Akademik

ЛАГРАНЖА УРАВНЕНИЯ

ЛАГРАНЖА УРАВНЕНИЯ: 1) в гидромеханике — ур-ния движения жидкости (газа) в переменных Лагранжа, к-рыми являются координаты ч-ц среды. Получены франц. учёным Ж. Лагранжем (J. Lagrange; ок. 1780). Из Л. у. определяется закон движения ч-ц среды в виде зависимостей координат от времени, а по ним находятся траектории, скорости и ускорения ч-ц. Обычно этот путь исследования оказывается достаточно сложным, и при решении большинства гидромеханич. задач используют Эйлера уравнения гидромеханики. Л. у. применяют гл. обр. при изучении колебат. движений жидкости.

Л. у. являются ур-ниями в частных производных и имеют вид:

где t — время, х, у, z — координаты ч-цы, a1, а2, а3 — параметры, к-рыми отличаются ч-цы друг от друга (напр., начальные координаты ч-ц), X, Y, Z — проекции объёмных сил, р — давление, r — плотность.

Решение конкретных задач сводится к тому, чтобы, зная X, Y, Z, а также начальные и граничные условия, найти х, у, z, р, r как функции t и a1, a2, a3. При этом надо использовать ещё неразрывности уравнение (тоже в переменных Лагранжа) и ур-ние состояния в виде r=f(р) (для несжимаемой жидкости r=const).

2) В общей механике — ур-ния, применяемые для изучения движения механич. системы, в к-рых за величины, определяющие положение системы, выбирают независимые между собой параметры, наз. обобщёнными координатами. Получены Ж. Лагранжем в 1760.

Движение механич. системы можно изучать, используя или непосредственно ур-ния, к-рые даёт 2-й закон динамики, или получаемые как следствия из законов динамики общие теоремы (см. ДИНАМИКА). В первом случае необходимо решать большое число ур-ний, зависящее от числа точек и тел, входящих в систему; кроме того, эти ур-ния содержат дополнит. неизвестные в виде реакций наложенных связей (см. СВЯЗИ МЕХАНИЧЕСКИЕ). Всё это приводит к большим матем. трудностям. Второй путь требует применения каждый раз разных теорем и для сложных систем приводит в итоге к тем же трудностям.

Л. у. дают для широкого класса механич. систем единый и достаточно простой метод составления ур-ний движения. Большое преимущество Л. у. состоит в том, что число их равно числу степеней свободы системы и не зависит от кол-ва входящих в систему точек и тел. Напр., машины и механизмы состоят из многих тел (деталей), а имеют обычно одну-две степени свободы; следовательно, изучение их движения потребует составления лишь одного-двух Л. у. Кроме того, при идеальных связях из Л. у. автоматически исключаются все неизвестные реакции связей. По этим причинам Л. у. широко используются при решении мн. задач механики, в частности в динамике машин и механизмов, в теории колебаний, теории гироскопа. В случае, когда на систему действуют только потенциальные силы, Л. у. приводятся к виду, позволяющему использовать их (при соответствующем обобщении понятий) не только в механике, но и в др. областях физики.

Для голономных систем Л. у. в общем случае имеют вид:

(d/dt)(дT/дq'i)-дT/дT/qi=Qi (i=1, 2, 3,...n) (1)

где qi — обобщённые координаты, число к-рых равно числу n степеней свободы системы, q'i — обобщённые скорости, Qi — обобщённые силы, Т — кннетич. энергия системы, выраженная через qi и q'i.

Для составления ур-ний (1) надо найти выражение Т (qi, q'i,t) и определить по заданным силам Qi. После подстановки Т в левые части ур-ния (1) будут содержать координаты qi и их первые и вторые производные по времени, т. е. будут дифф. ур-ниями 2-го порядка относительно qi. Интегрируя эти ур-ния и определяя постоянные интегрирования по начальным или краевым условиям, находят зависимости qi(t), т. е. закон движения системы в обобщённых координатах.

Когда на систему действуют только потенц. силы, Л. у. принимают вид:

(d/dt)(дL/дq'i)-дL/дqi=0 (i=1, 2,...,n) (2)

где L= Т -П — т. н. Лагранжа функция, а П — потенц. энергия системы. Эти ур-ния используются и в др. областях физики — электродинамике, статистич. физике и др.

Ур-ния (1) и (2) наз. ещё Л. у. 2-го рода. Кроме них, есть Л. у. 1-го рода, имеющие вид обычных ур-ний в декартовых координатах, но содержащие вместо реакций связей пропорциональные им неопределённые множители. Особыми преимуществами эти ур-ния не обладают и используются редко, гл. обр. для отыскания реакций связей, когда закон движения системы найден другим путём, напр. с помощью ур-ний (1) или (2).

ЛАГРАНЖА УРАВНЕНИЯ

гидромеханики - дифференциальные ур-ния движения частиц несжимаемой идеальной жидкости в переменных Лагранжа (см. Гидроаэромеханика), имеющие вид

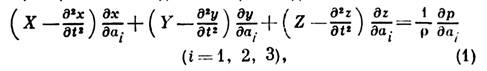
где t - время, х, у, z - координаты частицы жидкости, a₁, а ₂, а₃ - параметры, с помощью к-рых отличают частицы среды друг от друга (этими параметрами могут быть значения координат х₀, у₀,z₀ в нек-рый момент времени t₀), X, У, Z - проекции объёмных сил, р - давление, 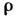- плотность. Получены Ж. Лагранжем (J. Lagrange) ок. 1780.

Решение общей задачи гидромеханики в переменных Лагранжа сводится к тому, чтобы, зная X, У, Z, а также начальные и граничные условия, определить х, у, z, р,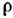как ф-ции времени и параметров a_l,a₂, a₃. Для решения этой задачи необходимо к ур-ниям (1) присоединить ур-ние неразрывности, имеющее в переменных Лагранжа вид и ур-ние состояния 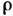=f (р) для баротропного движения или = const для несжимаемой жидкости. Если зависимости х, у, z от a_l, a₂, a₃, t найдены, то траектории, скорости и ускорения частиц определяются обычными методами кинематики точки.

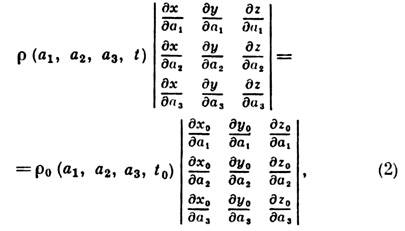
Обычно при решении задач гидромеханики пользуются Эйлера уравнениями. Л. у. применяются гл. обр. при изучении нестационарных движений, в частности колебат. движений жидкости, в нек-рых вопросах теории турбулентности.

Лит. см. при ст. Гидроаэромеханика. С. М. Таре.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.