LASERS
Les lasers (le mot «laser» est formé des initiales des mots anglais light amplification by stimulated emission of radiations , signifiant: amplification de lumière par émission stimulée de rayonnement) sont des sources nouvelles de rayonnement, mettant en œuvre une technique spéciale d’émission, dite «stimulée», par opposition à celle des sources usuelles de lumière, qui est «spontanée». L’intérêt des lasers tient à leur grande cohérence, c’est-à-dire à ce que leurs éléments engendrent des vibrations synchrones, pendant un temps très long par rapport à leur période, alors que, dans l’émission spontanée, de fréquents changements de phase interviennent, qui rendent incohérentes les lumières émises en des instants ou par des points même très voisins.
Les faisceaux émis par un laser permettent, par suite, de réaliser des interférences à grande différence de marche. Leurs rayons ayant tous sensiblement même direction, ils peuvent transmettre à grande distance cette énergie qui se disperse peu. Cette énergie peut au besoin être localisée en un très petit volume et y apporter, pendant un temps très court, une puissance très supérieure à celle qui est obtenue par d’autres moyens.
De nombreuses expériences antérieurement impossibles sont ainsi devenues réalisables. Aussi les lasers ont-ils fait l’objet de très nombreuses recherches, depuis que leur principe a été indiqué, en 1958, par C. H. Townes et A. L. Schawlow.
On s’est appliqué, en expérimentant des dispositifs très variés, d’une part, à diversifier les fréquences émises (d’abord peu nombreuses et situées dans le rouge et le proche infrarouge), d’autre part, à augmenter les énergies disponibles et leur concentration dans l’espace et dans le temps, à développer des applications telles que métrologie dimensionnelle de précision très accrue, portant parfois sur des distances énormes (entre Terre et satellites, par exemple), appréciation de très petits intervalles du temps, mesures spectroscopiques nouvelles, effets thermiques et biologiques des grandes énergies localisées (moyennant, bien entendu, des précautions contre leurs dangers), etc.
Les champs électromagnétiques très intenses réalisables à l’aide de lasers peuvent avoir sur la matière une action qui n’obéit pas à une loi de proportionnalité. L’optique non linéaire, qui met en œuvre de tels effets, offre des possibilités dont l’exploration commence à peine.
1. Principes et réalisations diverses
Émission spontanée et émission stimulée
On sait depuis Max Planck (cf. optique QUANTIQUE) que les atomes et les molécules peuvent posséder des énergies diverses W formant une suite discontinue, selon la position de leurs électrons par rapport aux noyaux. L’état fondamental est celui où W a la plus petite valeur possible, soit W1; les énergies plus grandes W2, W3 correspondent à des états excités, résultant du choc d’un autre atome ou de l’absorption d’un rayonnement (fig. 1 a). L’émission de lumière par la matière a lieu, comme l’a montré Albert Einstein, lors du passage brusque des atomes d’un état excité à un autre moins excité, ou à l’état fondamental. La fréquence du photon émis est:
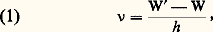
W et W étant les valeurs initiale et finale de l’énergie, et h la constante universelle de Planck:

Ce passage et l’émission du photon correspondant de fréquence 益 peuvent résulter de deux processus différents: l’émission spontanée et l’émission induite.
Dans le premier cas (fig. 1 b) le photon est émis dans une direction quelconque. L’instant d’émission est aléatoire. Sur un grand nombre N d’atomes dans l’état W , le nombre d N de ceux qui retombent à l’état W pendant le temps dt est:

AW W étant la probabilité d’émission spontanée par unité de temps.
Le second processus, l’émission induite, n’a lieu que si l’atome est soumis à un champ électromagnétique de même fréquence 益 que celle correspondant à la transition WW ou W W. La présence d’un tel champ provoque (induit) la désexcitation de l’atome de W , vers W, et donc l’émission d’un photon qui présente une propriété très remarquable: non seulement il a – par définition – la même fréquence que celle du champ inducteur, mais surtout il est émis en phase avec celui-ci, et dans la même direction. Après l’émission induite, par conséquent, rien ne permet de discerner le photon induit du photon inducteur, et ce phénomène est donc une véritable amplification du rayonnement inducteur (fig. 1 c).
Cependant, en pratique, la possibilité d’amplifier effectivement un rayonnement va dépendre de l’importance de l’émission induite. Einstein, qui en avait prévu l’existence en 1917, a montré que le nombre d N des transitions induites, pour un nombre N d’atomes dans l’état W , vaut:

où n est l’indice du milieu, c la vitesse de la lumière et I( 益) l’intensité du champ électromagnétique de fréquence 益 baignant l’atome, les BW W étant appelés les «coefficients d’Einstein» relatifs aux niveaux W ,W. L’émission induite apparaît ainsi comme le symétrique de l’absorption de la lumière par l’atome (fig. 1 a). Si, en effet, celui-ci se trouve au départ dans l’état W, un flux lumineux de fréquence 益 correspondant à l’écart W 漣 W provoquera des transitions WW , dont chacune prélève un photon du faisceau. Le nombre de ces transitions pendant un temps dt est proportionnel à l’intensité I( 益) du flux lumineux de fréquence 益 et au nombre N des atomes qui y sont soumis. Donc: d N = (n /c )BW,W I( 益)Ndt .
Or, d’après Einstein, BW,W = BW W [cf. ATOME]; nous pouvons donc décrire l’évolution d’un ensemble d’atomes dont N sont dans l’état W et N dans l’état W : si cet ensemble est éclairé par un faisceau lumineux d’intensité I( 益) à la fréquence 益, celui-ci va entraîner des transitions WW et W W. Chacune des premières absorbe un photon du faisceau, tandis que chacune des secondes le renforce d’un photon induit. Le faisceau ne sera donc amplifié que si: BW WN 礪 BW,W N et, puisque BW W = BW,W , alors N 礪 N. (On ne tient pas compte, en première approximation, de l’émission spontanée qui, se dispersant dans toutes les directions, ne contribue pas de façon significative à l’intensité d’un faisceau parallèle.)
Un milieu amplificateur doit donc contenir, pour que l’opération soit possible, un nombre suffisant d’atomes dans l’état W . Or la théorie indique que, à une température absolue T, dans un milieu où est établi un équilibre thermique entre matière et rayonnement, les nombres N et N d’atomes, d’énergie respective W et W , sont entre eux dans le rapport:

k étant la constante de Boltzmann:

On peut montrer que, aux températures usuelles, N est, pour les fréquences optiques, toujours très inférieur à N et que, par suite, l’émission stimulée est négligeable en comparaison de l’émission spontanée.
Pour permettre le fonctionnement d’un laser, il faut rendre, au moins temporairement, N supérieur à N (on dit alors qu’on a réalisé une inversion de population). Cette opération a été comparée à un pompage, qui augmente l’énergie d’une masse d’eau en l’élevant au-dessus de son niveau primitif.
Le principe du pompage optique a été indiqué en 1949 par Alfred Kastler [cf. POMPAGE OPTIQUE]. Dans le premier modèle de laser, dit à trois niveaux, le milieu utile est un cristal de rubis rose (alumine contenant des traces d’ions chrome). Sa couleur, lorsqu’il est éclairé en lumière blanche, résulte d’une absorption de radiations vertes qui fait passer les ions de l’état fondamental W1 (fig. 2 a) à l’un des états W2 d’un ensemble de niveaux excités très voisins; la présence de cet ensemble, remplaçant un niveau unique, permet d’augmenter l’énergie emmagasinée. Au lieu de retourner très vite au niveau W1 par émission spontanée, cette énergie se trouve en grande partie cédée, du fait de chocs non radiatifs, à un niveau intermédiaire W3, dont les possibilités d’absorption directe, mais aussi d’émision spontanée W3 漣 W1, sont beaucoup plus faibles que pour W2 漣 W1. Le stockage ainsi réalisé en W3 permet une émission stimulée W3 漣 W1.
Dans d’autres cas (laser à quatre niveaux, fig. 2 b), l’émission se produit de W3 vers un niveau W4 intermédiaire entre W3 et W1, qui se vide rapidement vers W1 et dont la population reste ainsi relativement faible, ce qui permet une émission plus intense.
Cohérence et puissance
Les photons induits ont même direction et même sens de propagation que ceux qui stimulent leur émission. Pour obtenir un nombre suffisant de rencontres avec des atomes excités, il faut que le parcours des photons dans le milieu utile soit assez long, ce qu’on peut obtenir par des réflexions successives. On utilise à cet effet deux miroirs plans parallèles (ou un dispositif équivalent), comme dans l’interféromètre de Pérot et Fabry [cf. INTERFÉRENCES LUMINEUSES]. L’un de ces miroirs est aussi parfaitement réfléchissant que possible, l’autre légèrement transparent, pour laisser sortir le faisceau qu’on veut utiliser.
Ce dispositif rappelle celui des tuyaux sonores et celui des cavités résonantes utilisées dans la technique des ondes radioélectriques courtes. Des ondes stationnaires s’établissent entre les deux miroirs, dont la distance doit être un multiple entier k de la demi-longueur d’onde. Celle-ci étant ici de l’ordre du micron, k atteint 105 ou 106, et les ondes qui se stabilisent suivant la normale au miroir peuvent correspondre à un certain nombre de modes (valeurs diverses de k ) à l’intérieur de la largeur spectrale de la lumière de longueur d’onde. Cette largeur qui caractérise l’émission spontanée correspond, pour un gaz, à la largeur Doppler due à l’agitation thermique des atomes, pour les liquides ou solides, à une largeur déterminée par les actions intermoléculaires. Lorsque l’émission stimulée a lieu, la largeur des raies laser que l’on désignera par 嗀凞 est beaucoup plus petite que celle d’une source de lumière naturelle. La monochromaticité d’une raie laser – surtout d’un laser à gaz – est d’un degré de finesse que n’atteignait aucune des sources de lumière monochromatique précédemment connues. Un laser donné peut être multimodes. Il émet alors simultanément sur plusieurs modes voisins, correspondant chacun à un ordre d’interférence entier k , ces différents ordres étant situés à l’intérieur de la largeur d’émission spontanée. Il peut, dans certaines conditions, être monomode et ne donner lieu qu’à une raie laser unique située alors au voisinage du centre de la raie d’émission spontanée.
La largeur spectrale 嗀凞 n’est jamais nulle, car les niveaux d’énergie W et W subissent des fluctuations, mais elle est très petite: alors qu’il n’y a aucune relation de phase permanente entre les ondes émises spontanément par des atomes excités, l’émission induite se trouve en accord de phase avec celle qui la stimule (autrement dit, l’émission stimulée est très monochromatique). Elle se fait donc par trains d’ondes beaucoup plus longs que ceux des autres sources de lumière (ce qui la rapproche du fonctionnement des oscillateurs radioélectriques). On dit qu’elle présente une grande cohérence longitudinale (ou encore temporelle, cet adjectif traduisant la durée des trains d’ondes).
Deux faisceaux de longueur d’onde et de largeur spectrale, issus d’un même point et ayant parcouru des chemins optiques différents de d , ne peuvent produire des franges d’interférences d’ordre p = d / que si leur «coefficient de finesse»/ 嗀凞 est supérieur à p . Ce rapport, de l’ordre de 107 pour les radiations «naturelles» les plus fines, peut être des millions de fois plus grand pour les lasers.
La lumière de ceux-ci a, en outre, une très grande cohérence transversale (ou spatiale), ce qui signifie que des points situés normalement à la direction de propagation, à une certaine distance l’un de l’autre (plusieurs millimètres ou même davantage), sont encore en accord de phase et peuvent donner lieu à des interférences, contrairement à ce qui se passe pour les autres sources. Il sort ainsi d’un laser à miroirs plans dans la direction normale à ceux-ci une onde plane cohérente, l’ouverture du faisceau étant parfois réduite au minimum qu’imposent les phénomènes de diffraction. Cette directivité favorise une transmission de la lumière à grande distance.
Les lasers à rayonnement continu n’émettent, en général, qu’une puissance relativement faible: ce n’est qu’une petite fraction de la puissance fournie au dispositif de pompage. La plus grande part de l’énergie perdue est tranformée en chaleur dans la matière active. Pour limiter l’échauffement de celle-ci, et surtout pour obtenir (pendant des temps courts) une puissance libérée plus grande, on opère par impulsions en produisant le pompage optique par éclairs successifs; mieux encore, on supprime temporairement l’une des réflexions, puis on la rétablit brusquement quand le pompage a accumulé, au niveau voulu, une population très accrue d’atomes excités (lasers déclenchés). Un moyen d’y parvenir consiste à utiliser une cellule de Pocket pour interdire ou permettre la transmission en lumière polarisée. On a pu ainsi, avec des lasers au néodyme (cf. infra ), produire des émissions dépassant 1010 watts pendant quelques nanosecondes (10 size=1漣9 s).
L’émission comporte en général un certain nombre N d’oscillations sur des modes voisins; certains dispositifs assurent entre ceux-ci un couplage qui transforme ces N vibrations indépendantes d’amplitude A, donc de puissance A2, en une seule vibration de durée N fois moindre, mais d’amplitude NA, donc de puissance 2A2. On a atteint ainsi 1013 watts pendant 10 size=1漣13 s (lasers à modes synchronisés).
Les cavités et les modes lasers
Nous avons vu comment, pour assurer à l’onde lumineuse un nombre suffisant de rencontres avec les atomes excités, on lui faisait décrire des aller et retour successifs dans le milieu amplificateur en plaçant celui-ci entre deux miroirs. Cet ensemble constitue ce que l’on nomme, par analogie avec les cavités résonnantes utilisées en hyperfréquence, la «cavité» du laser, et la présence de cette cavité confère à la lumière émise par les lasers plusieurs de ses caractéristiques les plus essentielles, et en particulier la double «cohérence» caractéristique de ces sources: cohérence «temporelle» et cohérence «spatiale».
Les cavités à miroirs plans
Le cas des cavités formées de deux miroirs plans parallèles est particulièrement simple à étudier, puisque cette cavité est identique à l’interféromètre de Pérot et Fabry évoqué plus haut. Cependant, en pratique, l’obtention d’une inversion de population importante est toujours difficile, et l’amplification subie par l’onde lumineuse par unité de longueur est faible. Cela conduit à construire des cavités longues, en séparant beaucoup les miroirs. Or, en même temps, le pompage (optique ou autre) exige généralement que l’une au moins des dimensions du milieu amplificateur soit faible. Ce double impératif conduit à des cavités à la fois longues et étroites, mettant en œuvre des miroirs largement séparés et de faibles dimensions. Mais alors, un phénomène bien connu en optique: la diffraction (cf. LUMIÈRE – Diffraction) provoque, à chaque réflexion de l’onde sur les miroirs, son élargissement. Toute l’onde ainsi renvoyée n’atteint donc pas l’autre miroir, ce qui se traduit par des pertes importantes.
Il est ainsi très difficile de faire fonctionner un laser avec des miroirs plans, et la quasi-totalité des lasers utilisent au moins un miroir sphérique concave qui, à chaque passage de l’onde, la «reconcentre» et réduit ainsi très fortement les pertes par diffraction.
Les cavités à miroirs sphériques
On montre que les cavités à miroir(s) sphérique(s) favorisent, tout comme les cavités à miroirs plans, certaines ondes, qui en sont les modes.
Mais ces modes ne sont plus les ondes planes se propageant en faisceaux parallèles, caractéristiques des miroirs plans (ou de l’interféromètre de Pérot et Fabry). Ce sont des faisceaux dits «gaussiens», caractérisés par le fait que, à l’intérieur de leurs sections, l’amplitude du champ lumineux E obéit à une loi qui, dans le cas le plus simple (mode «fondamental» ou «axial»), est une loi de Gauss (d’où leur nom):

r étant la distance à l’axe, où le champ passe par un maximum E0, w mesure le rayon de la section transversale, puisque E tombe à 1/e 2 de sa valeur au centre lorsque r = w . En fonction de la propagation, w varie comme le montre la figure 3. On note que, de part et d’autre d’une section de diamètre minimal 2 w 0, appelée le «col» ou la «taille» du faisceau, celui-ci se dilate selon la loi:
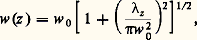
z étant la distance à la taille.
Loin de celle-ci, le faisceau gaussien présente la divergence totale: 2/ 神w 0. À cet étalement progressif du faisceau gaussien de part et d’autre de la taille correspondent des surfaces d’ondes sphériques, dont le rayon de courbure R, dans la section d’abscisse z , vaut  On notera que, pour z = 福0 = 神w 20/, R passe par un minimum égal à 2 福0.
On notera que, pour z = 福0 = 神w 20/, R passe par un minimum égal à 2 福0.
 On notera que, pour z = 福0 = 神w 20/, R passe par un minimum égal à 2 福0.
On notera que, pour z = 福0 = 神w 20/, R passe par un minimum égal à 2 福0. Modes des cavités à miroirs sphériques et faisceaux gaussiens
C’est l’existence de ces surfaces d’onde sphérique qui fait que les faisceaux gaussiens sont des modes des cavités à miroirs sphériques. En effet, si l’on imagine, dans un faisceau gaussien, deux surfaces d’ondes quelconques remplacées par des surfaces réflectrices, il est aisé de voir que, chacune renvoyant l’onde exactement sur elle-même, celle-ci va osciller indéfiniment entre ces miroirs, en se retrouvant – à une atténuation près – identique à elle-même après chaque aller et retour: or telle est bien la définition d’un mode.
À l’inverse, si l’on se donne deux miroirs de courbure R1 et R2, séparés de d , tout faisceau gaussien possédant, avec ce même écart, deux surfaces d’onde ayant ces courbures R1 et R2 sera un mode de la cavité formée par ces miroirs. On montre que l’on peut toujours trouver un tel faisceau à condition que R1, R2 et d respectent la double condition:

et cela signifie que ces miroirs peuvent alors constituer la cavité d’un laser. L’intérêt des cavités sphériques est leur commodité de réglage et elles sont très utilisées.
Cependant, si le gain de l’amplificateur est élevé, on peut s’affranchir de la condition ci-dessus, en constituant ce que l’on appelle une «cavité instable». Dans celles où l’élimination des modes transverses est facile, le même résultat peut être obtenu en conférant à l’un des miroirs un coefficient de réflexion décroissant du centre au bord, selon une loi, par exemple, gaussienne (cavité à miroir gaussien).
Mode fondamental et modes d’ordre supérieur
La condition définie ci-dessus étant respectée, on montre qu’il existe non pas un seul faisceau gaussien s’inscrivant entre les deux miroirs, mais une triple famille. La première correspond aux faisceaux décrits ci-dessus avec des longueurs d’onde telles que (k + 1/2) = 2d , k étant un entier quelconque. Chacun de ces faisceaux est un mode fondamental de la cavité (du reste, une condition analogue définissait – en ondes planes – les modes du laser à miroirs plans).
Les deux autres familles de modes, tout en conservant des surfaces d’ondes sphériques comme les premiers, ont une répartition du champ lumineux qui n’est plus gaussienne, mais présente une variation beaucoup plus complexe, avec une ou plusieurs annulations du champ selon chaque coordonnée. Ces modes, plus divergents que les modes fondamentaux, sont dits «modes d’ordre supérieur» ou «modes transverses». Dans tous les cas, les vecteurs champs électrique et magnétique des modes sont transverses à la direction de propagation. C’est pourquoi, par analogie avec les hyperfréquences, on les note TEMij (TEM pour transverse électrique magnétique). Les indices i et j , nombres d’annulations du champ d’action selon x et y dans une section du faisceau, sont les «ordres» de chaque mode. On a ainsi les modes TEM 00, 01, 10, 11, 20, 21... (photo 1), le mode fondamental étant le mode TEM 00.
Généralement, les modes d’ordre supérieur présentent plus de pertes que les modes axiaux et n’entrent en oscillation que lorsque le pompage est très intense. Néanmoins, c’est souvent ainsi que les lasers sont utilisés, et ces modes peuvent alors être gênants car ils contribuent, du fait de leur divergence supérieure à celle des TEM 00 (on le constate sur la photo 1), à élargir le faisceau émis. On peut généralement les supprimer en mettant à profit, précisément, cette divergence: un diaphragme disposé dans la cavité les affaiblit fortement, tout en n’atténuant que peu les modes axiaux, et l’on peut, par ce moyen, ne conserver que ceux-ci.
Des méthodes plus élégantes font appel, comme exposé ci-dessus, aux cavités instables, ou à «miroir gaussien». Dans tous les cas, on réalise un laser dit «monomode transverse».
Principaux types de lasers
Les lasers à cristaux
Les recherches qui se poursuivent activement font apparaître fréquemment des modèles nouveaux, de performances améliorées.
On a donné ci-dessus le principe du laser à trois niveaux, à cristal de rubis rose, qui fut réalisé en premier lieu par T. H. Maiman (1960). L’excitation résulte d’une décharge dans un tube à néon enroulé en hélice autour du cristal (fig. 4). Celui-ci, d’une longueur de quelques centimètres, a ses faces terminales (dont le diamètre est de quelques millimètres) planes, parallèles, et recouvertes de couches très réfléchissantes (l’une d’elles ayant cependant un facteur de transmission de quelques centièmes). La longueur d’onde émise est de 694,3 nm (rouge extrême) à la température ordinaire.
Un autre cristal particulièrement intéressant est le grenat d’yttrium et d’aluminium (Y3Al512), en abrégé Y.A.G., contenant en faible quantité du néodyme, qui est l’atome «actif». Alors que le rubis est un corps à trois niveaux, le néodyme met en jeu le pompage à quatre niveaux de la figure 2 b. De ce fait, la puissance requise pour le pompage est plus faible, et le rendement peut atteindre 3 p. 100, soit plus de dix fois celui du laser à rubis. L’émission du néodyme a lieu dans le proche infrarouge, à 1,06 猪m.
Pour le reste, la constitution des lasers à néodyme dans le Y.A.G. est comparable à celle des lasers à rubis, au point que certains systèmes laser peuvent recevoir indifféremment (avec éventuellement un changement de miroirs) un barreau de rubis ou de néodyme.
En ce qui concerne les énergies maximales émises, elles sont sensiblement proportionnelles au volume des barreaux, pouvant atteindre une centaine de joules à chaque éclair de pompage pour les plus gros rubis (face=F0019 歷 = 2 cm, L = 20 cm), et une cinquantaine de joules pour les plus gros cristaux de Y.A.G. (face=F0019 歷 = 2 cm, L = 10 cm). Il faut, bien entendu, que l’énergie fournie à la lampe éclair de pompage soit suffisante. La durée de l’émission laser dépend de celle du pompage. Elle est typiquement du même ordre (quelques millisecondes). Pendant ce temps, l’intensité émise n’est généralement pas uniforme, mais se présente plutôt comme une suite d’impulsions irrégulières (photo 2).
Le néodyme dans le Y.A.G. présente cependant un autre mode de fonctionnement: en effet, grâce au rendement de pompage relativement élevé, une émission continue est possible, à condition de pomper en continu, et de refroidir très énergiquement le cristal (et la lampe de pompage). On a pu ainsi engendrer, avec les plus gros cristaux, près de 1 kW en continu. Par ailleurs, on a évoqué plus haut le fonctionnement «déclenché» des lasers, obtenu, par exemple, lorsqu’une cellule de Pocket est intercalée entre l’amplificateur et l’un des miroirs. Les lasers à rubis et à néodyme se prêtent particulièrement bien au fonctionnement déclenché. Si les énergies émises ne sont qu’environ le dixième de ce que le même cristal fournirait en fonctionnement normal, la durée de l’émission est ramenée à quelques dizaines de nanosecondes seulement (fig. 5), ce qui conduit à des puissances considérables.
Les lasers à solides non cristallins
Bien que les milieux cristallins soient généralement les plus favorables à la réalisation de matériaux amplificateurs, ils présentent l’inconvénient d’être difficiles à fabriquer en grandes dimensions. Cela a conduit à rechercher des solides non cristallins, dont plusieurs se sont révélés capables de constituer des milieux amplificateurs. L’un des plus utilisés est le verre contenant une faible quantité de néodyme. Si les seuils de fonctionnement laser sont, à taille donnée, bien plus élevés que dans le Y.A.G., on sait, par contre, fabriquer avec le verre des lasers de gros volume (utilisant, par exemple, des barreaux de verre de 1 m de long et de 10 cm de diamètre), et c’est avec de tels lasers que l’on obtient les puissances les plus fortes que l’homme sache engendrer (cf. infra ).
Les lasers à gaz
Les lasers à gaz, bien que ne différant pas dans leur principe des autres types de lasers, présentent un certain nombre de caractéristiques qui leur donnent un intérêt particulier. Grâce à la nature même de l’état gazeux, l’amplification peut être obtenue par toute une variété de procédés d’excitation, qui sont employés seuls ou conjointement: décharges électriques, détente, pompage optique, réactions chimiques, etc.
La possibilité d’une inversion de population entre deux niveaux quantiques dépend de façon cruciale des vitesses de transfert des populations moléculaires ou atomiques dans l’ensemble des niveaux du système. Ces vitesses sont liées en partie aux interactions interatomiques ou intermoléculaires qui, dans le cas des gaz, dépendent essentiellement de la fréquence des collisions et de la nature des espèces moléculaires ou atomiques. L’expérimentateur est maître de ces paramètres puisqu’il peut choisir la température, la pression et la composition du gaz dans de larges limites.
L’excitation porte le gaz hors de l’état d’équilibre thermodynamique et, si les paramètres sont convenablement choisis, l’inversion de population apparaît parmi quelques-uns des nombreux niveaux quantiques des espèces constituant le gaz. En fait, un nombre considérable (plusieurs milliers) de raies d’émission laser ont été obtenues pour une soixantaine de gaz ou vapeurs, dans un domaine spectral s’étendant de l’ultraviolet à l’infrarouge lointain.
Dans les gaz à basse pression, les raies d’émission ont une largeur spectrale très réduite, et il est possible de stabiliser la fréquence de l’émission laser à l’intérieur de ces raies avec une précision inégalée, d’où l’importance que ces lasers viennent d’acquérir en métrologie.
Le renouvellement rapide du gaz et son homogénéité permettent d’obtenir, dans certains cas, des puissances continues bien plus considérables que dans tous les autres types de lasers, et déjà de nombreuses applications industrielles commencent à apparaître, telles que découpage de tôle, fusion de matières réfractaires, microsoudure, etc.
En bref, les lasers à gaz se distinguent par leur nombre élevé de raies disponibles, leur puissance continue et leur stabilité en fréquence.
L’effet laser est obtenu entre les niveaux quantiques de molécules, d’atomes ou d’ions constituant le gaz, ou la vapeur, placé entre les deux miroirs du résonateur optique. Les transitions entre niveaux électroniques, dans ces trois types d’espèces, donneront lieu à des émissions laser situées généralement dans l’ultraviolet et le visible, quelquefois dans le proche infrarouge. Les transitions entre niveaux de vibration-rotation des molécules donneront lieu à des émissions dans l’infrarouge moyen et lointain entre 3 猪m et 300 猪m (cf. tabl. 1). Décrivons les différents types de lasers à gaz.
Lasers fonctionnant sur des transitions électroniques
L’excitation du milieu gazeux dans les lasers fonctionnant entre des niveaux électroniques est obtenue par trois principaux moyens: décharge électrique dans le gaz, illumination par un rayonnement ultraviolet donné par une lampe éclair, faisceau d’électrons en impulsions brèves. Les mécanismes de fonctionnement de ces lasers sont très variés et pas toujours bien connus.
Le laser à hélium-néon, premier laser à gaz, découvert par A. Javan, est l’un des plus employés dans les applications pratiques. Ce laser émet de nombreuses raies, situées dans le visible et le proche infrarouge, sur des transitions électroniques du néon excité par un transfert d’énergie à partir de l’hélium.
Les deux transitions laser les plus intenses se situent l’une dans le rouge à 0,6328 猪m, l’autre dans l’infrarouge à 3,39 猪m (fig. 6 a). Les électrons libérés par la décharge électrique portent les atomes d’hélium sur l’état électronique noté par les spectroscopistes 21So. C’est un état métastable, c’est-à-dire que les atomes ne peuvent redescendre directement à l’état de base. Par contre, lors d’une collision d’un atome d’hélium excité avec un atome de néon, il peut s’effectuer un échange d’énergie : l’atome d’hélium descend à l’état fondamental et l’atome de néon est porté au niveau 3S2 dont l’énergie est voisine du niveau de l’hélium (transfert résonant). Les niveaux les plus bas 3p 4 et 2p 4 se dépeuplent plus rapidement que le niveau le plus haut 3S2, principalement par collision sur les parois du tube, de sorte qu’il s’établit une inversion de population donnant lieu à l’effet laser.
Une catégorie importante de lasers est représentée par les lasers à excimère . Un excimère est une molécule qui n’est stable que dans un état électronique excité. Un exemple en est donné par les halogénures de gaz rares comme les fluorures de krypton KrF ou de xénon XeF. L’excitation est réalisée par une décharge électrique ou un faisceau d’électrons dans un mélange de gaz rare et d’halogène, du fluor par exemple. Le fluor est décomposé en atomes qui réagissent sur les atomes de gaz rare excité pour former la molécule d’excimère. L’effet laser a lieu sur les transitions entre l’état excité stable et l’état de base dissociatif. L’inversion de population est donc très facilement réalisée, puisque l’état d’arrivée de la transition est très rapidement dépeuplé par dissociation de la molécule. Cette circonstance permet à ce type de laser d’atteindre des rendements énergétiques relativement élevés (jusqu’à 10 p. 100).
Un autre type de laser s’est révélé capable de fournir en impulsion des énergies considérables: le laser à iode atomique. Le principe en est le suivant: les iodures organiques du type R-I, où R est un radical aliphatique complètement fluoré, sont décomposés par le rayonnement ultraviolet d’une lampe éclair au xénon en donnant des atomes d’iode dans l’état électronique excité 2P1/2. Ces atomes retournent à l’état de base 2P3/2 par la transition optique 2P1/22P3/2 très lente lorsqu’elle est spontanée mais qui donne lieu à une émission laser très intense dans l’infrarouge proche de 1,315 猪m. Des impulsions laser transportant une énergie de 60 joules en 1 nanoseconde ont pu être obtenues avec ce type de laser.
Lasers fonctionnant sur des transitions de vibration-rotation
Un exemple important de laser fonctionnant sur des transitions de vibration-rotation est donné par le cas des lasers à C2-2.
Le gaz carbonique (CO2) possède trois modes de vibration, désignés par 益1, 益2, 益3, [cf. SPECTROSCOPIE]. L’énergie vibrationnelle dans chacun de ces modes est quantifiée suivant des niveaux de vibration, eux-mêmes subdivisés en niveaux de rotation. La molécule d’azote 2 ne possède évidemment qu’un mode de vibration, et son premier niveau de vibration ( 益 = 1) est très voisin du premier niveau, noté 0 0 0 1, du mode 益3 de C2 (fig. 6 b).
Une décharge électrique dans le mélange gazeux libère des électrons qui, par arrachement aux molécules C2 et 2 et retour à l’état neutre, excitent leurs niveaux de vibration. Or les modes 益1 et 益2 de C2 se désexcitent par collision beaucoup plus rapidement que le mode 益3 et que celui de 2. Il s’ensuit une inversion de population entre le niveau 0 0 0 1 du mode 益3 et les niveaux 0 2 0 0 ou 1 0 0 0 des modes 益1 et 益2, d’où l’émission de nombreuses raies laser sur les transitions de vibration-rotation correspondantes, vers 10 猪m. La puissance de ce type de laser est considérablement augmentée si l’on ajoute de l’hélium au mélange. L’hélium a un double rôle : il désexcite par collision moléculaire les niveaux d’arrivée 1 0 0 0 et 0 2 0 0 des transitions laser et favorise l’évacuation de la chaleur vers les parois du tube grâce à sa grande conductibilité thermique. Ce type de laser a un excellent rendement (de l’ordre de 20 p. 100), et la puissance d’émission peut atteindre couramment 500 watts. Des puissances de l’ordre de 500 kilowatts ont été atteintes par détente du gaz préalablement porté à haute température. La détente dans une tuyère «gèle» l’excitation vibrationnelle tandis que la température de translation s’abaisse fortement. On obtient ainsi un déséquilibre thermodynamique considérable.
À l’intérieur de chaque raie du laser à C2, la plage d’accord de l’émission laser est faible, de l’ordre de quelque 107 hertz, car la pression du gaz n’est pas assez forte pour élargir les raies par les collisions moléculaires. Pour certaines applications, notamment en spectroscopie, il est utile d’étendre cette plage d’accord en augmentant la pression du gaz. Cependant, en régime continu, une décharge électrique dans un gaz à pression élevée dégage beaucoup de chaleur qui détruit les conditions nécessaires à l’établissement d’une inversion de population. L’évacuation de cette chaleur peut néanmoins être réalisée par les parois de tubes laser à section très étroite, de l’ordre du millimètre carré. Ces lasers sont appelés lasers capillaires ou lasers guides d’ondes . Des lasers guides d’ondes ont pu permettre une plage d’accord allant jusqu’à 109 hertz sur chaque raie.
L’excitation peut être obtenue par des décharges électriques très brèves et très intenses dans le gaz à pression atmosphérique, entre des électrodes rapprochées de quelques centimètres et placées longitudinalement dans le tube. Ce type de laser, le T.E.A. laser (transversely excited atmospheric laser ), est capable de fournir des impulsions de quelques nanosecondes avec une puissance de plusieurs watts, la puissance crête atteignant 1010 watts. Ces performances rivalisent avec celles des lasers solides au néodyme, et les études sur ce laser sont poursuivies activement, notamment afin d’obtenir la fusion nucléaire contrôlée.
Par suite de la pression élevée utilisée dans le T.E.A. laser, la plage d’accord de fréquence peut atteindre 1010 hertz sur chaque raie. Il a même été possible d’utiliser des pressions allant jusqu’à 2.106 pascals. Dans ces conditions, les différentes transitions de vibration-rotation sont suffisamment élargies pour se recouvrir entièrement, et les émissions laser peuvent être accordées sur n’importe quelle longueur d’onde entre 9 et 13 猪m.
Certains lasers moléculaires à H2O (molécules d’eau) ou à HCN (acide cyanhydrique) émettent dans l’infrarouge lointain. Ils sont également excités par des décharges électriques. Leur technologie et leur principe de fonctionnement sont semblables à ceux des lasers à C2. Cependant, leur puissance est très inférieure.
Les lasers chimiques
Les lasers chimiques constituent une catégorie de lasers dont l’étude a fait l’objet d’un grand nombre de travaux. L’énergie nécessaire au fonctionnement du laser est fournie par une réaction chimique effectuée au sein du mélange gazeux dans le tube laser. Les produits de réaction sont excités sur des niveaux de vibration et peuvent donner lieu à l’effet laser, soit directement, soit par l’intermédiaire d’un transfert à une autre molécule, comme celle de C2. On a souvent besoin d’un apport d’énergie électrique non négligeable pour préparer la réaction, par exemple pour former des atomes d’oxygène à partir de l’oxygène moléculaire. Un exemple de laser chimique est donné par le laser à acide fluorhydrique HF dont le principe est le suivant: la réaction dans un mélange d’hydrogène et de fluor à basse pression est déclenchée par une décharge électrique, ou par un éclair lumineux qui libère par dissociation des atomes de fluor et d’hydrogène. Ceux-ci sont constamment régénérés par les réactions:

Les molécules d’acide fluorhydrique sont formées dans des états vibrationnels excités et donnent lieu à l’effet laser entre deux niveaux de vibration.
Signalons que des lasers ont pu fonctionner sur les molécules d’acide chlorhydrique HCl et de fluorure de deutérium DF par une excitation purement chimique, sans apport d’énergie électrique. Des puissances de 2 MW ont ainsi été atteintes.
Les lasers à liquides et les lasers à colorants
Pour différentes raisons, les liquides ne se sont pas révélés être de très bons amplificateurs laser, à l’exception notable de certains qui sont tous des colorants organiques. C’est donc surtout de ceux-ci que nous parlerons, et cela d’autant plus qu’ils présentent le gros intérêt d’être accordables, c’est-à-dire que l’on peut, contrairement à la plupart des autres lasers, en régler la longueur d’onde d’émission dans une plage étendue. Découverts en 1966, ces lasers ont bouleversé les méthodes de la spectroscopie tant par leurs performances que par les nouvelles techniques qu’ils ont permis de mettre en œuvre.
Dans les montages usuels, les colorants sont dilués dans des solvants liquides où ils sont excités par absorption de la lumière. Comme dans de nombreux systèmes lasers, le gain et, du même coup, la possibilité d’oscillation sont liés à la réalisation d’une inversion de population. Les molécules de colorants comportent le plus souvent un nombre important d’atomes, ce qui rend leur spectre d’émission ou d’absorption extrêmement complexe à analyser dans le détail. Elles sont le siège de nombreux mouvements de vibration et de rotation, qui se traduisent par l’apparition de niveaux d’énergie caractéristiques, en quantité d’autant plus grande que la molécule est plus complexe. Pour toutes les molécules de colorants, ces niveaux forment un continuum pour chaque niveau électronique (fig. 7). Pour simplifier, on peut considérer pratiquement qu’elles se trouvent toutes dans l’état (noté 1 sur la figure) de plus basse énergie. En présence d’un rayonnement lumineux de fréquence 益 appropriée, les molécules peuvent absorber un quantum d’énergie h 益 et être excitées dans un état (noté 2) de S1, tel que h 益 = E2 漣 E1 = E. Or ces niveaux (du type 2) ont une durée de vie extrêmement brève, de l’ordre de quelques picosecondes (10 size=1漣12 s), et les molécules relaxent très rapidement vers le niveau vibrationnel (noté 3) le plus bas de S1, par une transition non radiative. La durée de vie du niveau 3 est d’une dizaine de nanosecondes (10 size=1漣9 s) environ, de sorte que, si le pompage lumineux à la fréquence v est suffisamment intense, de nombreuses molécules pourront être accumulées dans l’état 3 et présenter une inversion de population avec l’un quelconque des états (noté 4) de S0, à l’exclusion de l’état 1. Cette possibilité de gain permet d’envisager une oscillation laser entre les niveaux 3 et 4, par un processus typique du laser à quatre niveaux. De la même façon qu’entre les états 2 et 3, les molécules relaxent très rapidement du niveau 4 vers 1, et le cycle peut recommencer. L’absorption ayant lieu entre l’état 1 de S0 et les états de S1, le spectre correspondant s’étend sur un domaine caractérisé par la largeur de S1; l’émission (la fluorescence) ayant lieu à partir du niveau 3 vers les états de S0, le spectre qui lui correspond s’étend sur un domaine caractérisé par la largeur de S0. L’émission correspond, en moyenne, à des différences d’énergie plus petites que pour l’absorption, et le spectre d’émission se trouve, par conséquent, décalé par rapport au spectre d’absorption vers les grandes longueurs d’onde: ainsi, l’oscillation laser n’est obtenue que pour les longueurs d’onde de fluorescence qui ne sont pas réabsorbées par les molécules. Comme dans les autres lasers, elle s’obtient en enfermant le milieu amplificateur dans une cavité optique résonnante. Comme elle peut avoir lieu sur un assez grand intervalle spectral, elle s’accroche en fait à la fréquence optique pour laquelle la courbe de gain présente un maximum. La largeur en fréquence de la courbe de fluorescence est de nature essentiellement homogène, ce qui se traduit par une tendance des molécules émettrices à coopérer et, par suite, conduit à ce que la plus grande partie de l’énergie d’excitation stockée soit restituée dans une raie d’émission unique. Pour déplacer cette fréquence, il suffit de modifier la courbe de gain en utilisant, par exemple, des éléments disperseurs à l’intérieur de la cavité, comme des prismes ou des réseaux, ou encore des filtres biréfringents. Si l’on veut n’obtenir l’oscillation que sur un mode unique de la cavité, il faut utiliser des filtres encore plus efficaces constitués par des interféromètres. Ces oscillateurs lasers fonctionnent les uns par impulsions, les autres en régime continu. Les premiers sont excités (pompés) soit par des lampes à éclairs, soit par des lasers pulsés à rubis, à néodyme, à azote, à excimères; les seconds sont pompés par des lasers continus à gaz ionisé, argon ou krypton (photo 3). L’amélioration continuelle des performances de ces lasers a conduit à un développement technologique récent de laser à colorant continu en anneau, dans lequel on n’a plus affaire à des ondes stationnaires mais à une onde progressive que l’on oblige à choisir un sens de propagation. Les développements les plus prometteurs concernent la recherche de colorants nouveaux permettant d’élargir la gamme de longueurs d’onde déjà disponible et qui s’étend continûment depuis le proche ultraviolet (340 nm) jusqu’au proche infrarouge (1 000 nm). Les familles de colorants les plus connues sont les coumarines, les xanthènes, les cyanines, etc. Les puissances lumineuses disponibles sont très variables selon les types de lasers, les colorants, les solvants, les dilutions, les intensités de pompage, etc. On a pu obtenir avec les colorants les plus efficaces (par exemple la rhodamine 6G) jusqu’à 30 p. 100 de conversion de l’énergie de pompage. Une variété particulièrement intéressante de lasers à colorants fonctionnant par impulsions est constituée par les lasers à modes couplés (ou bloqués) qui délivrent des trains d’impulsions séparés par le temps d’un aller et retour dans la cavité ( 福 = 2L/c ), chaque impulsion ayant une durée de 1/ v de l’ordre de la picoseconde où v représente la largeur de la courbe de gain. De tels lasers picosecondes à colorants, fonctionnant en régime continu comme en excitation périodique, sont particulièrement adaptés aux expériences de spectroscopie résolue en temps et, de façon générale, aux études de phénomènes à relaxation très rapide. Récemment un tel laser, mettant en œuvre une cavité en anneau, a émis des impulsions de 70 . 10 size=1漣15 seconde.
Nous allons maintenant décrire d’autres lasers qui, comme les lasers à colorants déjà décrits, présentent l’intérêt d’être accordables: lasers à centres colorés, lasers paramétriques et, enfin, diodes lasers à semi-conducteurs et lasers Raman.
Notons d’ailleurs que, hormis les lasers accordables à proprement parler, les lasers offrent de nombreuses possibilités d’émettre de la lumière cohérente à des longueurs d’ondes diverses, en utilisant, notamment, les phénomènes non linéaires de conversion de fréquence décrits plus loin. Mais ces procédés requièrent de grandes puissances lumineuses; en outre, ils ne permettent pas de couvrir le même spectre qu’avec les lasers accordables (fig. 8).
Les lasers à centres colorés
Bien que les principes qui président à l’obtention d’une inversion de population soient très spécifiques dans le cas de cristaux qui présentent des centres colorés, on peut trouver de nombreuses analogies avec les molécules de colorants organiques. Il s’agit en particulier de systèmes à quatre niveaux; en outre, la nature de l’élargissement de la bande d’émission (luminescence) est essentiellement homogène. Les puissances lumineuses nécessaires au pompage de ces lasers sont relativement modestes, environ trente fois moindres que celles requises pour les colorants les plus efficaces: en tenant compte des pertes de cavité, on est conduit pratiquement à des taux de conversion de l’ordre de 2 à 3 p. 100.
Les centres colorés (ou centre F , de l’allemand Farbzentrum ), qui donnent lieu à une oscillation laser continue et accordable sur une large bande spectrale, sont créés dans des cristaux d’halogénures d’alcalins, dopés d’ions étrangers constitués par un autre métal alcalin. Les exemples les plus typiques sont donnés par des cristaux de chlorure de potassium dopés avec du lithium ou avec du sodium, ou encore par les cristaux de chlorure de rubidium dopés au lithium ou au sodium. Les centres F , dont il est question, proviennent tous de la vacance d’un anion dans le cristal, vacance dans laquelle un électron vient se piéger. L’électron ainsi fixé peut être excité optiquement par absorption d’un photon à partir de l’état fondamental de type s jusqu’au premier état excité de type p . Cependant, le système dans cet état excité est fortement instable et relaxe très rapidement (en quelques picosecondes) vers un état d’énergie inférieure, qui correspond à un réarrangement géométrique des ions autour de la vacance, donc sans émission lumineuse; en configuration relaxée, il émet un photon qui le désexcite et provoque de nouveau un réarrangement des ions entourant la vacance qui le ramène de façon non radiative vers l’état fondamental (fig. 9). Suivant la nature du centre F , il est possible ou non d’observer une inversion de population efficace entre les niveaux de la configuration relaxée, et d’obtenir un gain sur cette transition. On distingue généralement les centres F A et les centres F B, et, parmi eux, ceux du type I (à une vacance) et ceux du type II (à deux vacances en position relaxée). Seuls les centres F du type II donnent un effet laser. Dans les centres F A, l’un des six ions métalliques qui entourent la vacance est un ion étranger. Les centres F A de type II relaxent après une excitation optique, en une configuration de vacance à double puits de potentiel (schématisée figure 9). Dans les centres F B, deux des six ions entourant la vacance sont des ions étrangers. On obtient de tels centres en dopant le cristal en ions étrangers à de plus fortes concentrations.
D’une façon générale, la technologie de ces lasers est très semblable à celle qui est utilisée pour les lasers à colorants. Ils couvrent, pour le moment, la région du proche infrarouge située entre 2 et 3 猪m, mais l’espoir est grand de voir de nouveaux types de centres colorés (centres F 2, par exemple) qui permettraient d’étendre le domaine jusque vers 0,9 猪m pour les petites longueurs d’onde et 4 猪m pour les grandes.
Les lasers paramétriques
Contrairement à de nombreux oscillateurs lasers, le gain dans un oscillateur paramétrique n’a pas son origine dans une inversion de population entre des niveaux atomiques ou moléculaires. Il provient de l’interaction entre des champs électromagnétiques et un milieu optique non linéaire. D’une façon très générale, lorsqu’un système physique (mécanique ou électronique) est soumis à une excitation périodique de fréquence v , il suscite la génération d’harmoniques de cette fréquence dès lors que le signal de réponse du système est une fonction non linéaire du signal d’entrée. Ainsi, dans un milieu optique, si un champ fort (champ de pompage) de fréquence vp interagit avec un champ plus faible (champ signal) de fréquence vs , un nouveau champ est induit à la fréquence vi , telle que vi = vp 漣 vs . On peut dire encore que l’onde de fréquence vp module le paramètre caractéristique du milieu qu’est la susceptibilité linéaire, et induit un couplage avec l’onde de fréquence vs . Mais ce champ vi interagit à son tour avec le champ de pompage, ce qui accroît le champ signal: c’est le processus de l’amplification paramétrique qui accroît les champs aux fréquences vs et vi au détriment du champ de pompage. La relation vp = vs + vi exprime simplement la conservation de l’énergie.
Il est possible de calculer le gain pour chacun des champs de fréquence vs et vi . On trouve que ce gain est maximal lorsque 轢kp = 轢ks + 轢ki ; cette relation (condition d’accord de phase) exprime la conservation de l’impulsion (k = 2 神nv /c ; n : indice du milieu; c : vitesse de la lumière dans le vide). Lorsque cette condition est satisfaite, les trois ondes se propagent dans le milieu sans changement de leur phase relative initiale. La condition d’accord de phase peut être remplie en tirant parti des propriétés de biréfringence du milieu, soit que la propagation des ondes se fasse de manière colinéaire, soit non colinéaire (fig. 10).
Pour obtenir un oscillateur paramétrique, il suffit de placer le cristal non linéaire dans un résonateur optique exactement semblable à ceux utilisés pour les lasers usuels. Ces résonateurs peuvent être résonnants soit pour l’onde signal seule, soit pour les deux ondes vs et vi à la fois. Le balayage en fréquence d’un tel oscillateur s’effectue en agissant simultanément sur un paramètre physique du cristal non linéaire (température, orientation), de manière à modifier la condition d’accord de phase, et sur la longueur du résonateur.
Les matériaux utilisés dans des oscillateurs paramétriques sont principalement: le phosphate de potassium di-hydrogène (KDP), le phosphate d’ammonium di-hydrogène (ADP), l’arséniate d’ammonium di-hydrogène (ADA), l’iodate de lithium (LiIO3), le niobate de lithium (LiNbO3), le niobate de baryum-sodium (Ba2NaNb515); les trois premiers couvrent le domaine du proche ultraviolet et du visible, les trois autres celui du visible et de l’infrarouge proche et moyen. Au total, il est possible de couvrir pratiquement tout le spectre entre 0,25 猪m et environ 20 猪m. Les lasers de pompage les plus couramment employés sont les lasers à néodyme, à rubis et à colorants. Le mode de fonctionnement le plus répandu est celui par impulsions, mais on a pu montrer la possibilité de fonctionner en régime continu.
Les diodes lasers à semi-conducteurs
Les semi-conducteurs se distinguent des autres milieux actifs en ce qu’ils présentent des transitions radiatives entre des états liés (bande de valence) et des états libres (bande de conduction).
De nombreuses méthodes d’excitation (pompage) ont été utilisées pour obtenir une émission stimulée à partir de semi-conducteurs, qu’il s’agisse d’une excitation optique ou d’un bombardement électronique, ou encore d’une excitation par injection d’un courant dans une jonction p-n polarisée électriquement, etc. Sans entrer dans le détail de ces méthodes, on peut comprendre le mécanisme de cette émission stimulée en décrivant simplement les propriétés spectroscopiques des semi-conducteurs au moyen de deux bandes continues d’énergie: la bande de valence et la bande de conduction, séparées par une bande interdite de largeur EG. À l’équilibre, seule la bande de valence est peuplée d’électrons, la bande de conduction est vide. Sous l’effet d’une excitation quelconque, un certain nombre d’électrons passent dans la bande de conduction. À une température non nulle, la répartition des porteurs de charges (trous et électrons) a tendance à se diluer dans le matériau, mais il est possible, en supposant que les porteurs de charges d’une bande déterminée sont en équilibre thermique les uns avec les autres, de trouver des conditions pour lesquelles on obtient encore de l’émission stimulée.
Considérons, par exemple, une jonction p-n . Si on applique au système une tension de polarisation convenable V0, la barrière de potentiel étant réduite, des électrons de la zone n peuvent passer dans la zone p , où ils effectuent une transition vers un niveau vide de la bande de valence en émettant un photon d’énergie voisine de EG (ou inférieure à cause des impuretés). On peut aussi avoir une migration des trous vers la région n et une recombinaison avec des électrons, le processus prédominant étant essentiellement déterminé par les densités relatives d’impuretés, les durées de vie des porteurs et leurs mobilités. Mais, dans l’un ou l’autre cas, on peut trouver, pour un potentiel de polarisation V0 assez grand, une région active dans le voisinage de la jonction qui présente une inversion de population. Comme cette région est généralement très mince, on obtiendra un gain lumineux maximal sur un parcours raisonnable, dans le plan de la jonction proprement dite. D’où la structure géométrique de la cavité laser correspondant à une diode laser: les faces du cristal sont polies et forment les miroirs de la cavité (fig. 11). En général, les dimensions de la cavité sont si petites (quelques centaines de 猪m) que seul un mode peut osciller. Le domaine d’oscillation est fixé grossièrement par la composition du cristal; le balayage continu et fin de la fréquence est ensuite assuré usuellement, soit par variation du courant de polarisation, soit par variation de la température. De tels systèmes fonctionnent en régime pulsé aussi bien qu’en régime continu. Ils permettent aujourd’hui de couvrir la région du rouge (vers 0,7 猪m) jusqu’à l’infrarouge moyen (vers 35 猪m), mais ne délivrent que des puissances lumineuses moyennes relativement basses, de l’ordre de quelques dizaines à quelques centaines de mW seulement.
Les diodes lasers à semi-conducteurs qui ont été les plus employées sont : arséniure de gallium ou d’indium, antimoniure d’indium, etc., d’une façon plus générale les composés III-V et II-VI, en référence aux colonnes de la classification périodique des éléments (cf. classification PÉRIODIQUE).
Les lasers Raman à retournement de spin
Le principe sur lequel repose le fonctionnement de cette classe de lasers accordables est la diffusion stimulée par des électrons dans un semi-conducteur. Suivant ce principe de base, une lumière incidente de fréquence vp est diffusée à une fréquence v R telle que v R = vp 梁 E/h , selon qu’il s’agit de raies Stokes ou anti-Stokes (cf. effet RAMAN). L’effet Raman à retournement de spin (en anglais: spin flip Raman process ) implique un processus au cours duquel le spin d’un électron de la bande de conduction du cristal semi-conducteur est renversé par rapport à la direction d’un champ magnétique externe B. Dans ce cas, E = g . 猪B . B, où g est le rapport gyromagnétique effectif de l’électron (qui peut prendre des valeurs élevées dans un environnement cristallin), et 猪 size=1隣 le magnéton de Bohr. Le balayage en fréquence est alors aisément réalisé par variation continue de l’intensité du champ magnétique B. Ainsi, la grande valeur de g dans les semi-conducteurs (de l’ordre de 50 dans l’antimoniure d’indium) conduit à des domaines de balayage de près de 5 000 gigahertz pour des champs magnétiques allant jusqu’à 100 kilogauss.
Comme on peut l’imaginer, cet effet Raman s’apparente à l’émission lumineuse qu’on obtient dans les cristaux paramétriques et, dans ce cas aussi, il n’est pas nécessaire d’établir une inversion de population pour obtenir un gain lumineux. La condition de conservation de la quantité de mouvement est aisément remplie ici car une partie de la quantité de mouvement incidente est partagée entre un photon et un électron, au lieu d’être partagée entre deux photons; en particulier, on peut choisir d’observer la diffusion Raman stimulée à un angle quelconque avec le faisceau laser de pompage (fig. 12).
On peut montrer théoriquement que la section efficace de diffusion Raman à retournement de spin augmente de façon résonnante lorsque l’énergie des photons de pompage s’approche de la valeur EG de l’intervalle d’énergie de la bande interdite qui sépare la bande de valence de celle de conduction. Pour cette raison, ces lasers ne fonctionnent actuellement que dans l’infrarouge proche, avec des longueurs d’onde de pompage délivrées par les lasers à monoxyde de carbone (CO) [entre 5,2 et 6,5 猪m] et par les lasers à gaz carbonique (CO2) [entre 9 et 14,6 猪m]. Dans le cas du pompage à 5,3 猪m d’un cristal d’antimoniure d’indium par un laser à CO, le gain lié à la proximité de la longueur d’onde avec l’intervalle de la bande interdite est tel qu’il autorise un fonctionnement en régime continu, tandis qu’à 10,6 猪m le fonctionnement est en régime pulsé.
D’actives recherches sont en cours pour essayer d’étendre ce type de lasers à de nouvelles régions du spectre. Dans cet ordre d’idée, des résultats prometteurs ont déjà été obtenus avec des cristaux de sulfure de cadmium (CdS) dans le visible, en pompant avec une raie bleue intense d’un laser à argon ionisé.
Les lasers stabilisés en fréquence
Caractères de l’émission et de l’absorption
À l’exception des lasers guides d’ondes et T.E.A., la plupart des lasers à gaz fonctionnent avec des gaz sous faible pression, de l’ordre de quelques torrs. Dans ces conditions, les raies d’absorption ou d’émission du gaz présentent un élargissement dû principalement à l’effet Doppler (élargissement dit inhomogène): les molécules sont soumises à l’agitation thermique, elles ont des vitesses réparties suivant une distribution statistique de Maxwell et absorbent ou émettent à des fréquences différentes suivant leur vitesse. Il en résulte que, pour les transitions donnant lieu à une émission laser, la courbe donnant le coefficient d’amplification g du rayonnement en fonction de la fréquence 益 présente un profil Doppler donné par l’équation:
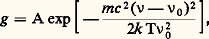
où 益0 est la fréquence du centre de la raie, k la constante de Boltzmann, m la masse de la molécule et c la vitesse de la lumière. Les miroirs du laser forment une cavité résonnante caractérisée par des modes de résonance correspondant aux fréquences pour lesquelles la distance entre les miroirs est un multiple entier de demi-longueurs d’onde. L’énergie lumineuse se trouve concentrée dans les fréquences de ces modes, mais pour que l’effet laser apparaisse il faut de plus qu’il y ait au moins un mode dont la fréquence se situe à l’intérieur de la courbe d’amplification, dans une région où l’amplification est supérieure aux pertes (fig. 13). Les molécules, dont la composante des vitesses suivant l’axe du tube laser (vitesse longitudinale) est telle que la fréquence de l’onde lumineuse qu’elles peuvent émettre est identique à celle d’un mode, vont donc se désexciter en fournissant de l’énergie à ce mode.
Si la fréquence 益1 de ce mode est différente de la fréquence 益0 du centre du profil Doppler (correspondant à une vitesse longitudinale nulle), les molécules émettant à cette fréquence 益1 possèdent soit la vitesse longitudinale v1, soit la vitesse longitudinale opposée 漣 v1; v1 correspond aux molécules émettant dans une direction et 漣 v1 dans la direction opposée. Donc, si l’on trace la courbe des populations en fonction des vitesses longitudinales, le mode v1, qui peut être considéré comme constitué par la superposition d’ondes se propageant en sens inverse à cause de la réflexion sur les miroirs, creusera deux trous dans cette courbe de population en induisant la désexcitation par émission de photons des molécules possédant les vitesses v1 et 漣 v1. Ces trous ont une certaine largeur due aux interactions des molécules entre elles (élargissement dit homogène). L’intensité d’émission laser est proportionnelle au nombre de molécules enlevées, donc à la surface des trous. Lorsque la fréquence du mode est déplacée, par changement de la longueur optique de la cavité, les deux trous se réduisent à un seul lorsque le mode coïncide avec le centre de la raie (cas 益1 = 益0), car alors 益1 = 0. La surface de ce trou est inférieure à la somme des surfaces des deux trous (cas 益1 益0) et l’intensité de l’émission est réduite. Le profil de l’émission présente donc un minimum à la fréquence 益 = 益0. Ce phénomène, calculé par W. E. Lamb, est appelé Lamb dip. Il peut être observé en absorption dans un gaz différent de celui du laser. En effet, si un gaz à basse pression, non excité, est traversé par deux ondes laser se propageant en sens inverse et de même fréquence, ce qui est facilement réalisé en plaçant la cuve à gaz à l’intérieur de la cavité laser, le profil d’absorption dans une raie du gaz étranger présente un minimum, lorsque la fréquence des ondes laser coïncide avec la fréquence du centre de la raie. Les raisons en sont les mêmes que précédemment, à cela près que les trous sont creusés dans les populations par pompages de molécules sous influence du rayonnement laser. C’est le phénomène d’«absorption saturée», dont l’utilisation en spectroscopie a pris un développement considérable.
Stabilisation des lasers et métrologie
Par un dispositif d’asservissement agissant sur la longueur de la cavité optique du laser, l’émission peut être stabilisée soit au centre du Lamb dip de la raie laser elle-même, soit au centre du Lamb dip d’une raie d’un gaz étranger, en absorption saturée. La précision sur la fréquence d’émission peut atteindre 10 11 et est suffisamment grande pour que l’on envisage d’employer une raie laser comme étalon de longueur, en remplacement de la raie d’émission du krypton 86 qui sert actuellement à la définition du mètre.
Déjà, à la suite de travaux poursuivis notamment au Bureau international des poids et mesures à Sèvres sur le laser à hélium-néon, les longueurs d’onde de la raie à 3,39 猪m, stabilisée sur une raie d’absorption du méthane, et de la raie à 0,6328 猪m, stabilisée sur une raie d’absorption de la vapeur d’iode, sont suffisamment bien mesurées par des méthodes interférométriques de comparaison à la longueur d’onde étalon du krypton pour pouvoir servir d’étalon secondaire.
Mesure de la vitesse de la lumière
La vitesse de la lumière dans le vide c est liée à la fréquence 益 et à la longueur d’onde par la relation très simple c =益. La fréquence de la raie du laser à hélium-néon à 3,39 micromètres, stabilisée sur le méthane, a été mesurée par le National Bureau of Standards, à Boulder (États-Unis), en utilisant une horloge à césium comme étalon de temps (cf. MESURE - Étalons fondamentaux). Par suite des différences considérables des fréquences entre l’horloge à césium et la raie à 3,39 micromètres, il a été nécessaire d’établir une chaîne de fréquences intermédiaires constituée par deux klystrons et des lasers à HCN, à H2O et à C2, soigneusement stabilisés. Ces comparaisons de fréquence entre les maillons de la chaîne se font par des techniques d’hétérodynage. Le résultat de cette mesure, multiplié par la longueur d’onde () déterminée comme on l’a vu précédemment, fournit d’emblée une valeur de la vitesse de la lumière connue à mieux que 1 mètre par seconde près: c = 299 792 458 m/s. Cela représente une amélioration des résultats antérieurs d’un facteur supérieur à cent.
2. Applications des lasers à la physique et dans l’industrie
Un avantage essentiel des lasers par rapport à toute autre source lumineuse est que la lumière, étant émise en faisceau, peut être acheminée, pratiquement sans pertes, vers l’utilisation. Cependant, dans un faisceau gaussien, la lumière n’émane pas d’un point, et ne peut donc être reconcentrée ponctuellement, ce qui conduit à une optique un peu particulière.
Optique des faisceaux gaussiens
Un faisceau gaussien, après traversée d’une lentille, redonne naissance à un autre faisceau gaussien. Par suite, au lieu des familières conjugaisons de point à point, on conjugue plutôt, en optique des faisceaux gaussiens, les tailles P1 et P2 de ces faisceaux (fig. 14).
Si p 1 et p 2 sont les distances des tailles «objet» et «image» à la lentille, de focale f , et, en posant:
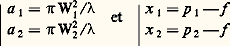
Lorsque W1 est très petit, a 1 est très inférieur à x 1, et l’on retrouve les relations relatives aux conjugaisons de points.
Moyennant ces relations, le faisceau laser peut être transformé à volonté, soit pour éclairer une toute petite zone, où il engendrera une intensité lumineuse considérable, soit, au contraire, pour être acheminé à très grande distance, en un faisceau quasi cylindrique (cf. LUMIÈRE – Diffraction).
Ces diverses possibilités ont suscité un grand nombre d’applications que nous allons évoquer. Toutefois l’holographie, qui utilise largement les lasers, ne sera pas traitée ici mais dans la rubrique relative à l’optique cohérente (cf. OPTIQUE - Optique cohérente).
Éclairage, alignement, guidage
Afin d’obtenir des éclairements très intenses, on focalise un faisceau laser sur la région à étudier; ces éclairements peuvent être aussi très brefs: jusqu’à 10 size=1漣14 seconde grâce aux lasers dits à modes synchronisés (mode-locked , cf. sufra ). Utilisés en photographie ulra-rapide, ces éclairs servent également à l’étude de certains comportements des molécules: réactions chimiques, diffusions, polarisation, etc., dont la rapidité interdisait jusqu’à présent l’étude dynamique. Parmi les phénomènes qu’est susceptible de provoquer le flux laser, figure en bonne place l’excitation de certaines molécules, qui deviennent à leur tour susceptibles d’amplifier (ou d’engendrer) un rayonnement de fréquence voisine ou inférieure à celle du flux excitateur, comme nous l’avons vu à propos des lasers à colorants.
On peut aussi, grâce au laser, éclairer des objets très lointains: des photographies de satellites distants de 1 500 km ont été ainsi obtenues avec un laser à rubis de 50 J.
Les militaires utilisent cette propriété pour désigner une cible lointaine à l’attention du tir terrestre ou aérien ou de fusées qui se dirigent de façon automatique vers l’objet éclairé.
On peut aussi asservir un engin à se déplacer le long d’un faisceau laser: un engin antichar sera ainsi guidé comme par un fil vers le char adverse, une machine de forage creusera en ligne droite malgré les irrégularités de la roche.
Tous les éclairages par laser ne sont pas aussi élaborés: il existe, dans les laboratoires, des milliers de petits lasers continus pour les réglages et les alignements d’éléments optiques ou mécaniques.
Plus simples et encore bien plus nombreux sont les lecteurs de codes barres, dans lesquels un mince faisceau laser (généralement He-Ne ou semi-conducteur), démultiplié par des miroirs tournants multiples, balaye l’espace traversé par les objets à identifier, tandis qu’un détecteur analyse le signal retour pour y repérer un code. Plusieurs centaines de milliers de tels appareils sont vendus chaque année.
Enfin, dans deux autres secteurs encore plus proches du grand public, le marché du laser a véritablement explosé. Il s’agit des «imprimantes laser», où un faisceau laser très fin, dévié par des miroirs, vient impressionner le papier pour y tracer, point par point, les graphismes seulement limités par la capacité du microprocesseur qui commande le mouvement du miroir, et par la vitesse de balayage des miroirs. Or le pinceau fin du laser permet d’utiliser des miroirs très petits et donc très rapides. Plusieurs millions de ces imprimantes, utilisant comme source des diodes lasers d’une fraction de watt, sont vendus chaque année.
Pour terminer, mentionnons pour mémoire l’application maintenant la plus connue du laser: le lecteur de disques compacts, dans lequel le faisceau d’une diode laser d’environ 1 mW éclaire un disque en rotation dont le pouvoir de réflexion en chaque point est codé en fonction de l’information (son, images, signaux informatiques) à restituer. Dans certains cas, l’enregistrement est possible par la même méthode: des dizaines de millions de ces appareils sont produits chaque année.
Éclairage et vision en milieu absorbant
L’observation à travers un milieu absorbant n’est généralement pas limitée par le phénomène d’absorption proprement dit; en fait, le récepteur est aveuglé par la lumière de la source diffusée par les couches les plus proches, tout comme un automobiliste dans le brouillard est aveuglé par la lumière de ses propres phares.
Supposons alors que la source émette des impulsions très brèves et que la réception ne soit effectuée que durant un intervalle de temps très court survenant t secondes après l’émission: on n’observera en retour que le seul rayonnement ayant cheminé t secondes depuis l’émission, rayonnement provenant d’une «tranche» du paysage située à la distance ct /2. La lumière renvoyée par les couches proches, en particulier, est entièrement éliminée. Cette méthode a été utilisée avec succès pour l’observation des fonds portuaires: les eaux, continuellement brassées par les hélices, y sont toujours chargées de vase et limitent la vision à quelques décimètres, alors que le laser déclenché permet l’observation jusqu’à plusieurs dizaines de mètres.
Soudure et usinage des matériaux
Dans les applications qui précèdent, l’état de surface de l’objet visé n’est pas modifié par le flux laser (sauf pour les réactions photochimiques), et l’on peut parler d’éclairement. Il n’en est plus de même lorsqu’on concentre suffisamment le faisceau lumineux.
La partie du flux incident, qui n’est pas renvoyée mais absorbée par le corps, devient capable d’élever de façon notable sa température superficielle: l’impulsion de 1 J d’un petit laser à rubis, concentrée sur un diamètre de 0,1 mm, représente un flux de 12 MW/cm2 si l’impulsion dure 1 ms. Ainsi, même un laser relativement modeste, concentré sur une très petite surface, peut y créer localement des températures très élevées.
Focalisés sur des aires du même ordre, des lasers plus puissants permettent d’atteindre des températures auxquelles aucun matériau, même «réfractaire», ne résiste.
De plus, cet apport d’énergie, très intense mais très localisé, provoque la fusion (voire la volatilisation) très rapidement, sans que la chaleur ait le temps de se propager notablement: on réduit ainsi fortement les phénomènes collatéraux (déformation, corrosion, recristallisation), qui affectent, par exemple, la découpe ou la soudure au chalumeau ou à l’arc. Typiquement, un laser Nd-Y.A.G. de 1,5 à 2 kW coupe une plaque métallique d’acier doux, inox, alliage léger, de 5 mm d’épaisseur à des vitesses de l’ordre de quelques mètres par minute, et un laser C2 de 10 kW obtient les mêmes résultats jusqu’à plus de 1 cm d’épaisseur.
À plus faible vitesse, on peut couper (ou souder) des épaisseurs plus importantes. Des lasers beaucoup moins puissants sont utilisés pour couper, à très grande vitesse, les matériaux non conducteurs: tissus, papiers, matières plastiques, verres. C’est pourquoi un nombre croissant de lasers (surtout CO2 et Nd-Y.A.G.) sont utilisés dans l’industrie pour des applications qui représentent, en valeur, le tiers du marché (civil) total de tous les lasers.
Mesure des distances
Les lasers déclenchés ont permis de réaliser des dispositifs que, par analogie avec le radar (radio detection and ranging ), on a appelé lidar (light detection and ranging ). Le principe consiste à envoyer vers l’objet dont on veut connaître l’éloignement une impulsion lumineuse très courte. Une partie de cette lumière, diffusée par l’objet, revient vers le point d’émission où elle est recueillie. Du temps t séparant l’émission du retour de l’écho, on tire la distance d de l’objet à l’observateur par la relation d = 2 t /c .
La cohérence du laser présente là un double avantage: le faisceau émis étant très fin, il s’ensuit non seulement une portée élevée, mais aussi une bonne définition du point cible. C’est ainsi que, dans les premiers appareils de ce genre réalisés – des télémètres de char –, le laser indique la distance du point qui se trouve exactement à la croisée de fils matérialisant l’axe de la lunette.
Depuis ces premières réalisations, l’augmentation de la cadence de fonctionnement des lasers a permis d’utiliser des lidars pour reconstituter, point par point, de véritables images en relief des objets observés. De tels lidars existent maintenant pour toute une variété d’applications, depuis le guidage des petits robots, jusqu’au repérage et à l’identification de cibles militaires à très grande distance.
On s’intéresse ensuite à des objets plus lointains: les satellites terrestres et la Lune. Il convient là, plus encore que dans les applications terrestres, de mettre à profit la cohérence du laser pour émettre un pinceau très fin dont une fraction notable sera interceptée par la cible. Toutefois, il n’est plus alors question de laisser cette énergie diffuser dans toutes les directions comme dans le cas précédent. Il faut, au contraire, en renvoyer la plus grande partie dans la direction de l’émetteur au moyen de réflecteurs spéciaux: les cataphotes, qui se présentent comme trois miroirs deux à deux perpendiculaires. Des satellites ainsi équipés (on dit qu’ils sont «coopératifs») renvoient un écho suffisant pour que l’on puisse déterminer leur distance à 0,1 m près jusqu’à plus de 3 000 km. En effectuant à plusieurs reprises des mesures simultanées depuis trois stations au moins, on peut déterminer avec une très haute précision (de un à quelques centimètres) leurs positions relatives.
On peut obtenir des mesures aussi précises en prenant cette fois pour cible un cataphote déposé sur la Lune, et plusieurs ont déjà été déposés à cet effet sur notre satellite.
Interférométrie et métrologie
Si toutes les applications que l’on vient d’évoquer font appel essentiellement à la cohérence spatiale des lasers et à la concentration de l’énergie qu’elle rend possible, d’autres mettent à profit leur cohérence temporelle. Un moyen simple est de superposer l’onde émise à un instant donné avec l’onde émise à un instant antérieur. Pour cela, le faisceau émis en L est séparé en deux parties, dont l’une parcourt une distance supérieure à l’autre d’une longueur l = 2 d avant qu’on ne les confonde à nouveau. Si, au cours du temps nécessaire pour parcourir la distance l , la fréquence de l’onde est restée la même, les deux ondes superposées ont encore la même fréquence et elles peuvent, selon que 2 d contient ou non un nombre entier de longueurs d’onde, se renforcer ou s’annuler réciproquement en D: on dit que les ondes interfèrent, et le montage optique dédoublant puis recombinant les ondes est appelé interféromètre (fig. 15).
On peut ainsi mesurer la distance d , ou plutôt ses variations: il suffit pour cela de construire un interféromètre dans lequel on prend pour d la longueur à mesurer elle-même. Puisque, chaque fois que l contient un nombre entier de, l’éclairement à la sortie de l’interféromètre passe par un maximum, il suffit de compter ceux-ci pour mesurer les variations de d .
La fréquence – et donc – étant parfaitement définie, d sera connu avec la même précision. On commence à utiliser maintenant des interféromètres éclairés par des lasers pour mesurer aussi bien des distances courtes: étalonnage, voire traçage automatique des règles, déplacements de machines-outils, déformations de toutes sortes, etc., que des intervalles très grands, dépassant parfois le kilomètre pour l’étude des déformations de l’écorce terrestre. La précision relative, qui dépasse couramment 10 size=1漣7 et peut atteindre 10 size=1漣13, place d’emblée le laser parmi les instruments les plus puissants de la métrologie.
Cependant, au-delà de quelques mètres, et surtout en plein air, la précision (de l’ordre de 1) de l’interféromètre est excessive, car la turbulence de l’air provoque des fluctuations continuelles en D, faussant ainsi les mesures.
On constitue alors «artificiellement» une onde de plus grande longueur d’onde L1 en modulant électriquement le faisceau laser à la fréquence 1 = C/L1.
Le même raisonnement que ci-dessus montre que, en D (fig. 15), la lumière passera par un maximum chaque fois que 2 d est multiple de L1. Comme L1 拾 1, on a donc bien réalisé l’interféromètre moins sensible cherché.
Mais, surtout, on peut, en faisant varier F, mesurer la distance d sans avoir à la décrire, ou à la modifier. Il suffit pour cela d’ajuster 1 successivement sur deux valeurs voisines 1 et 2 conduisant chacune à un maximum d’éclairement en D.
Si L1 et L2 sont les longueurs d’onde correspondantes, on aura:

d’où l’on tire:

puis d . Plusieurs appareils commerciaux, d’emploi quasi instantané, utilisent ce principe, et des milliers d’entre eux sont employés par les géomètres et les topographes.
Télécommunications par laser
Lumière très monochromatique et émise en étroits pinceaux, le laser serait un excellent support d’information, et cela d’autant plus que sa fréquence très élevée (de l’ordre de 10 14 Hz) autorise qu’on le module jusqu’à plus de 10 10 Hz: des milliers de canaux de télévision, des millions de voies téléphoniques pourraient ainsi être acheminés simultanément. Cependant, la propagation des ondes dans l’atmosphère nécessiterait des points d’émission et de réception élevés, et pourrait de surcroît être perturbée par les intempéries. On s’est affranchi de ces contraintes en faisant propager le faisceau dans des fils de verre de très faible diamètre qui canalisent l’onde lumineuse comme les guides d’onde canalisent les ondes hertziennes. Après plusieurs années de recherche, on est parvenu à obtenir des verres très purs et presque parfaitement transparents, dans lesquels l’atténuation des ondes lumineuses n’est plus due qu’à l’inévitable diffusion de la lumière pour les molécules du milieu.
Ce phénomène est d’autant plus faible que la longueur d’onde est grande, ce qui conduit à se placer dans l’infrarouge; le choix précis de la longueur d’onde résultant alors d’un compromis entre les lasers disponibles (toujours pratiquement des diodes lasers) et la dispersion de l’indice du matériau constituant la fibre.
Typiquement, on atteint maintenant des atténuations de l’ordre de 1 p. 100 par kilomètre. Après de premières liaisons, installées entre des centraux téléphoniques distants de quelques kilomètres, on en est venu à des liaisons à grande distance, par exemple pour le câblage de Biarritz puis de très nombreuses villes françaises, et maintenant sont réalisés les premiers câbles transatlantiques à fibres [cf. TÉLÉCOMMUNICATIONS].
Mesure des vitesses
Mesure des vitesses linéaires
On sait depuis longtemps, avec les radars par exemple, mesurer les vitesses en mettant à profit l’effet Doppler, c’est-à-dire la variation de fréquence subie par une onde électromagnétique lors de sa réflexion sur un objet en mouvement.
Si l’onde incidente est caractérisée par le vecteur d’onde 轢ki (fig. 16), l’onde diffusée dans la direction d’observation par le vecteur 轢kr , l’effet Doppler se traduit par un décalage d 益 de la fréquence de l’onde diffusée:
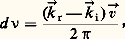
轢v étant la vitesse de l’objet.
La difficulté pratique réside, pour les ondes électromagnétiques, dans la valeur très faible du décalage relatif d 益/ 益. De ce fait, ces mesures n’étaient pas accessibles aux sources lumineuses habituelles, dont l’étalement spectral 益, bien supérieur à d 益, masque totalement le décalage. Par contre, sa largeur spectrale très faible fait du laser une source idéale pour de telles mesures.
Encore faut-il mesurer le décalage. Une méthode particulièrement appropriée est de «mélanger» (cf. infra ) une partie de la lumière incidente servant à l’éclairage, et la lumière diffusée.
Mesure des vitesses angulaires. Lasers en anneaux
Dans la cavité laser habituelle, la lumière décrit des aller et retour entre deux miroirs en revenant sur elle-même. Cependant, rien n’empêche d’imposer aux rayons lumineux un trajet polygonal quelconque, par exemple triangulaire avec trois miroirs M1, M2, M3 (fig. 17). D’après le principe du retour inverse, le trajet imposé aux rayons par les miroirs peut être décrit dans les deux sens, et il apparaît deux ondes oscillantes tournant en sens inverse.
Si, lorsque le triangle est immobile, ces deux ondes parcourent la même longueur et ont la même fréquence, il n’en est plus de même dès que le triangle est animé d’une rotation: l’onde tournant dans le même sens doit parcourir une distance un peu plus grande pour se raccorder à elle-même, et celle tournant en sens inverse une distance un peu plus courte. Les longueurs d’onde de chacune de ces oscillations, liées aux distances parcourues, seront ainsi modifiées, ce qui se traduira par une légère variation affectant, en plus et en moins, leur fréquence initiale commune.
Si on les superpose sur un détecteur D, on observe au cours du temps une succession de battements. La fréquence de ces battements est proportionnelle à la vitesse angulaire de rotation de l’ensemble qui peut donc constituer un gyromètre à la fois précis et totalement dépourvu de toutes pièces mobiles.
Depuis plus de dix ans, la plupart des avions sont équipés en série de tels gyromètres, dont plus d’une centaine de milliers sont maintenant en service. Des missiles et des lanceurs, comme Ariane, en sont également munis. Un montage analogue a permis de répéter, avec une précision mille fois plus grande, la célèbre expérience de Michelson et Morley, confirmant ainsi la constance de la vitesse de la lumière [cf. RELATIVITÉ].
Phénomènes non linéaires. Mélanges de fréquences
Le champ électrique lumineux très intense apparaissant lorsqu’on focalise un faisceau laser peut provoquer des ruptures diélectriques au sein des matériaux. Cependant, même lorsqu’il n’atteint pas le seuil d’arrachement des électrons, ce champ leur impose sa vibration. Les électrons ainsi sollicités émettent de la lumière à la même fréquence: c’est la diffusion Rayleigh.
Lorsque l’amplitude de la vibration imposée cesse d’être petite par rapport aux dimensions atomiques ou, ce qui revient au même, lorsque le champ lumineux excitateur n’est plus négligeable vis-à-vis du champ d’attraction du noyau sur les électrons, le mouvement de ceux-ci cesse d’être exactement sinusoïdal à l’image du champ excitateur, mais présente une distorsion: le comportement du milieu vis-à-vis de la lumière n’est plus linéaire.
On peut considérer le mouvement ainsi déformé comme la somme d’une vibration sinusoïdale à la fréquence excitatrice et de vibrations de fréquences double, triple...
Chacune d’entre elles, d’après les lois de l’électromagnétisme, rayonnant de la lumière, on constate que le milieu, éclairé à une fréquence 益, rayonne, en plus de la diffusion normale de même fréquence 益, de la lumière à 2 益, 3 益...
Un raisonnement analogue montre que, si l’on envoie sur le milieu deux vibrations 益1 et 益2 dont l’une au moins est de très grande amplitude, le milieu va émettre de la lumière aux fréquences 2 益1, 3 益1, 2 益2, 3 益2, 益1 = 益2, ... (en général |m 益1 + n 益2|, m et n étant des entiers).
Il s’en faut que ces phénomènes, déjà complexes, suffisent à décrire le comportement des matériaux. L’irradiation provoque en effet, dans certains cas, des variations de l’indice de réfraction, c’est-à-dire de la vitesse de l’onde elle-même, ce qui entraîne une concentration spontanée (autofocalisation) du faisceau.
En outre, l’interaction d’une onde laser intense avec certaines vibrations spontanées du milieu ou des molécules qui le constituent peut donner lieu à une émission lumineuse présentant tous les caractères d’une oscillation laser, mais à des fréquences s’écartant de 益 de valeurs caractéristiques du matériau: ce sont les émissions Brillouin et Raman stimulées.
L’apparition du laser, première source lumineuse cohérente, et la mise en évidence de matériaux (ADP, KDP, NbO3Li, ...) fortement non linéaires pour les ondes lumineuses permettent d’envisager la transposition à l’optique des techniques de la radioélectricité: multiplication de fréquence, redressement, amplification paramétrique, battements et détection hétérodyne dont on connaît l’apport irremplaçable aux télécommunications.
Sur le plan pratique, on utilise aujourd’hui couramment des doubleurs de fréquence pour transformer l’émission à 1,06 猪m des lasers à néodyme en un rayonnement à 0,53 猪m beaucoup plus facile à détecter.
Un cas un peu différent, mais très important en pratique, d’interaction entre ondes lumineuses est le «mélange de fréquences»: lorsque plusieurs ondes (par exemple 益1 et 益2) parviennent simultanément sur le même détecteur lumineux (lequel, étant sensible à l’intensité – et donc au carré du champ électrique lumineux –, est, par essence, non linéaire vis-à-vis des amplitudes), un calcul simple montre que le courant détecté comporte, là encore, toutes les fréquences m 益1 梁 n 益2. Ces fréquences ne sont toutefois observées que si le détecteur est assez rapide pour les «suivre ». Généralement, aux fréquences optiques, ce n’est pas le cas, et seule la composante | 益1 漣 益2| – si 益1 et 益2 sont assez proches – est observable. Tel est le cas pour les mesures Doppler (cf. supra ), où cette méthode de mélange est très utilisée.
Spectroscopie résolue en temps avec les lasers femtosecondes
Parmi les qualités des sources lasers les plus réclamées par les scientifiques et les industriels, il faut citer celles qui permettent d’émettre le maximum de longueurs d’onde soit en continu, soit de façon impulsionnelle et, dans ce cas, avec les durées les plus courtes possibles.
Ces besoins ont conduit aux lasers dits femtoseconde (fs), l’une des réalisations les plus spectaculaires de ces dernières années. Grâce à leur brièveté, ces lasers, de durées d’impulsion de 10 size=1漣13 à 10 size=1漣14 s (= de 100 à 10 fs), ont permis d’engendrer par effets non linéaires une gamme continue de longueurs d’onde, s’étendant pratiquement de l’ultraviolet au proche infrarouge. Cela donne à ces lasers une énorme potentialité pour faire de la spectroscopie résolue dans le temps.
Cette course passionnante vers les temps ultracourts a permis de gagner près de quinze ordres de grandeur par rapport à l’échelle temporelle humaine de la seconde, alors que, en parallèle, la course vers les petites dimensions spatiales ne portait que sur dix ordres de grandeur, de la taille humaine du mètre vers celle de l’atome, avec le dixième de nanomètre.
Dans ces conditions, les lasers femtosecondes, en offrant les plus brèves quantités d’énergie (6 fs) que l’on puisse faire interagir avec la matière, ouvraient une nouvelle voie expérimentale très prometteuse vers l’interaction laser-matière en autorisant des puissances crêtes supérieures au petawatt (1015 W). Les intensités espérées dépasseront bientôt 1020 W/cm2, avec des installations dont l’encombrement est sans commune mesure avec le gigantisme de certaines installations lasers mises en place pour étudier la fusion thermonucléaire contrôlée.
Afin de mieux saisir les domaines d’intérêt ouverts par les lasers femtosecondes, il est utile de schématiser la manière d’étudier les évolutions rapides de certaines interactions lumière-matière. Pour cela, on fait appel à une méthode inspirée directement de la stroboscopie, technique utilisée depuis des lustres pour étudier facilement les mouvements les plus rapides, par un astucieux ralentissement apparent des phénomènes. Cette méthode de spectroscopie résolue en temps, dite «pompe-test», consiste à envoyer successivement dans le milieu à étudier deux impulsions lumineuses dont la seconde est continûment retardable par rapport à la première. Celle-ci, l’impulsion «pompe», est intense afin d’initier le phénomène à étudier dans l’échantillon ainsi excité (ou pompé), tandis que la seconde, l’impulsion «test», éventuellement accordable, explore le milieu excité par des mesures d’absorption, d’émission, de réflexion ou de tout autre phénomène optique... visualisant ainsi l’évolution temporelle des phénomènes créés dans l’échantillon. Généralement, cette exploration nécessite plusieurs longueurs d’onde différentes pour tester spectroscopiquement l’échantillon. Or les effets non linéaires évoqués plus haut permettent d’engendrer, à partir des impulsions initiales amplifiées, tout un «continuum spectral» composé d’impulsions toujours femtosecondes s’étendant continûment du proche infrarouge à l’ultraviolet. Il suffit, pour cela, de focaliser dans un milieu transparent (de l’eau par exemple) les impulsions femtosecondes amplifiées pour créer le continuum spectral relativement lissé et dont la durée reste dans les domaines des femtosecondes. Utilisé comme «test», ce continuum, en arrivant avant, pendant, et après les impulsions «pompes», permet une spectroscopie, résolue à l’échelle des temps les plus brefs que l’on sache maîtriser à l’heure actuelle.
Les impulsions de ces lasers vont jouer dans cette spectroscopie plusieurs rôles fondamentaux et très spécifiques, celles-ci devant obligatoirement satisfaire les critères suivants: être un «flash lumineux» suffisamment intense pour initier le phénomène à étudier; engendrer d’une manière synchrone toutes les longueurs d’onde nécessaires à une étude spectrale; être stables et répétitives pour étudier les phénomènes au cours de leurs évolutions ultrarapides.
Rappelons que, au niveau microscopique, quand une molécule se dissocie sous l’effet de la lumière, les fragments libérés peuvent s’éloigner les uns des autres à près d’un kilomètre par seconde, ce qui signifie que, en 100 fs, la liaison chimique qui les maintenait ensemble s’est distendue puis a fini par céder. Les lasers femtosecondes permettent de suivre en direct les étapes intermédiaires de cette rupture. C’est de façon identique que des phénomènes beaucoup plus complexes sont disséqués, qu’il s’agisse du comportement des électrons dans différents milieux, par exemple dans les semi-conducteurs, matériaux constituant les transistors et les piles solaires. De même, dans un liquide aussi commun que l’eau, la spectroscopie résolue dans le temps apporte une meilleure compréhension des transferts d’électrons à travers les membranes biologiques. Les premières étapes de la photodissociation des protéines ont pu être appréhendées avec ces techniques, de même que celles de la photosynthèse qui transforme la lumière en énergie chimique avec un rendement excellent, que l’on aimerait rencontrer dans nos usuels convertisseurs d’énergie! Tous les processus ultrarapides en physique, en chimie et en biologie sont ainsi devenus accessibles grâce à cette spectroscopie femtoseconde, avec en plus, ces toutes dernières années, une course très prometteuse vers les très hautes intensités.
La recherche des fortes intensités a été une préoccupation constante depuis la naissance du laser. Si l’on étudie la courbe des puissances dispensées par les lasers depuis 1960, on note une spectaculaire progression dans la période 1960-1970, correspondant à la mise au point des lasers déclenchés et des lasers à modes bloqués donnant des impulsions dans les domaines micro, nano et subnanoseconde. Après un palier de plus de quinze ans, il faut attendre 1985 pour voir une nouvelle technique permettre d’amplifier des impulsions lasers très courtes sans que les puissances instantanées mises en jeu ne détériorent les matériaux utilisés: il s’agit de l’amplification d’impulsion à dérive de fréquence (en anglais C.P.A. pour chirped pulse amplification : transposition d’une technique radar utilisée depuis 1960). Cette amplification d’impulsion à dérive de fréquence consiste en un étirement temporel (d’un facteur 103 à 104) de l’impulsion laser ultrabrève dans un milieu dispersif, puis une amplification maximale de cette impulsion étirée, sans craindre alors des non-linéarités gênantes, puisque les puissances crêtes sont réduites des mêmes ordres de grandeur que ceux de l’étirement, et enfin une compression à la sortie du milieu amplificateur, pour retrouver la durée initiale, tout en essayant de conserver une grande partie de l’énergie amplifiée.
De cette manière on peut obtenir des énergies supérieures de plusieurs ordres de grandeur à celles qui sont obtenues dans les amplifications classiques. Les impulsions femtosecondes bénéficient d’un facteur 1013 à 1015 par rapport au continu. Cette énergie peut être concentrée sur une toute petite surface seulement limitée par les lois de la diffraction de l’optique, et, à un taux de récurrence de 10 à 20 Hz, des intensités de 1019 W/cm2 sont déjà atteintes. Dans un très proche avenir, les 1020 ou 1021 W/cm2 n’apparaissent plus hors de portée, à des taux de récurrence élevés et dans des installations d’encombrement très réduit. Une dernière hypothèse laisse à penser que la fusion thermonucléaire contrôlée par confinement inertiel dans les grands lasers de puissance pourrait être assistée par une impulsion très énergétique dans le domaine temporel des femtosecondes.
Cette ouverture vers les très hautes intensités donne aussi l’espoir de réaliser des expériences relativistes dans lesquelles les cibles irradiées par les lasers femtosecondes se trouveront dans un état où le champ électrique associé à l’impulsion laser excitatrice sera de plusieurs ordres de grandeur supérieur au champ coulombien des atomes constituant le matériau de la cible. Tous les phénomènes qui peuvent en découler ne sont pas encore répertoriés, certains pouvant être complètement inattendus. C’est ainsi une toute nouvelle physique qui s’ouvre, dès à présent, aux chercheurs, dans ce domaine de la physique ultrarapide avec, n’en doutons pas, de spectaculaires applications.
Mesures à distance des composants atmosphériques par absorption sélective
Un laser accordable (à colorants ou à semi-conducteurs) ou un laser capable d’émettre plusieurs raies (laser à C2) est utilisé pour explorer (par balayage continu point par point) le spectre atmosphérique. Pour cela, le (les) faisceau(x) laser sont envoyés à travers l’atmosphère. Certaines des longueurs d’onde étant plus absorbées que les autres par tel ou tel composant, on conçoit que, de l’analyse des intensités restantes aux diverses longueurs d’onde après traversée, on puisse remonter aux teneurs des composants rencontrés (qui devront bien sûr être moins nombreux que les longueurs d’onde utilisées).
L’avantage est que le faisceau fin et la puissance élevée du laser permettent une très grande sensibilité, même sur un long trajet.
Les mesures à distance par rétrodiffusion Rayleigh ou Raman
La méthode décrite ci-dessus présente l’inconvénient d’exiger la présence d’un récepteur (ou d’un déflecteur) à l’extrémité du trajet du faisceau. Seules les mesures au sol sont ainsi possibles. De plus, les teneurs relevées intègrent la totalité du parcours, excluant par exemple l’établissement de profils le long du trajet du faisceau.
Tel n’est pas le cas des méthodes de rétrodiffusion, qui utilisent la propriété qu’ont les corps (ici les gaz) de réémettre de la lumière dans toutes les directions lorsqu’ils sont eux-mêmes éclairés. Il existe deux sortes de diffusions : la diffusion Rayleigh , qui s’effectue sans changement de fréquence, et la diffusion Raman , qui s’effectue avec un changement de fréquence 益R propre à chaque molécule, ce qui permet d’en faire un instrument sélectif (cf. effet RAMAN, diffusion de la lumière RAYLEIGH).
La plupart des installations utilisant ce principe fonctionnent comme des radars optiques : l’impulsion lumineuse très brève d’un laser déclenché est envoyée dans l’atmosphère, dont les «tranches» successives renvoient, par diffusion, de la lumière dans toutes les directions, et en particulier vers un récepteur placé à côté de l’émetteur.
La variation, en fonction du temps, de l’intensité de cette lumière permet de calculer la densité des molécules diffusantes en fonction de la distance.
Si l’observation a lieu à la même fréquence que celle du laser, on observe la diffusion Rayleigh (plus celle due aux poussières), qui, si elle donne une indication du nombre total des molécules présentes à chaque distance, ne permet pas de les identifier.
Cependant, si l’on recherche un seul composant, son identification devient possible à condition de relever en même temps deux profils. Si l’un est établi à une longueur d’onde coïncidant avec une raie d’absorption du composant, et l’autre à une longueur d’onde légèrement différente, la comparaison des deux conduit à la concentration cherchée. L’appareillage, dit Dial (differential absorption lidar ), doit comporter deux sources.
Une méthode plus générale permet l’identification de tous les composants atmosphériques. N’utilisant qu’un seul laser, elle consiste à observer la lumière rétrodiffusée à une fréquence décalée de 益R par rapport à celle du laser. On observe alors la diffusion Raman, spécifique à chaque molécule, et qui permet ainsi de relever le profil de concentration de la molécule choisie le long du trajet. Cet appareillage, dit Lidar Raman (photo 4), présente un intérêt pour les mesures météorologiques (fig. 18) et la lutte antipollution, puisque plusieurs composants peuvent être mesurés avec le même laser (il suffit d’utiliser plusieurs détecteurs observant aux décalages 益R appropriés).
La mesure des températures
La diffusion Raman évoquée ci-dessus donne naissance, dans la plupart des molécules, non pas à une seule, mais à tout un ensemble de réémissions (raies) décalées de n R, n R, N R, ... (écarts tous caractéristiques de la molécule) par rapport à la fréquence de la lumière incidente.
Or l’intensité relative de ces raies dépend de la température, et l’on utilise maintenant ce moyen pour effectuer, en instantané si le laser est assez puissant, des mesures de température de gaz, même dans des endroits très peu accessibles: jets de tuyère, brûleurs, chambres de moteur à explosion.
La séparation isotopique
Les divers isotopes ont donc des propriétés chimiques identiques et sont donc très difficilement séparables chimiquement. Or l’uranium naturel est un mélange d’isotopes dont les noyaux comportent respectivement (pour 92 protons) 143 et 146 neutrons, dont seul le premier, qui ne représente que 0,7 p. 100 du minerai, est utilisable dans les réacteurs nucléaires. Il faudrait donc l’isoler ou, tout au moins, élever sa concentration dans l’uranium qui sera utilisé. Tel est le but de la séparation isotopique (cf. séparation isotopique et retraitement NUCLÉAIRE).
La séparation par laser repose sur le fait que la différence de masse des noyaux, lorsqu’on passe d’un isotope à un autre, se traduit par un très léger décalage entre les niveaux d’énergie correspondants E et F (ou entre position des raies spectrales – cf. SPECTROSCOPIE), comme l’illustre la figure 19.
Grâce au laser, qui émet, contrairement aux autres sources lumineuses, une longueur d’onde parfaitement définie, il est alors possible d’exciter l’un des isotopes – A par exemple – si la fréquence d’émission du laser correspond à la fréquence 益1 de la raie de A.
La photoionisation
Il reste à séparer physiquement l’isotope ainsi excité. Pour cela, on utilise encore un laser, dont l’énergie h 益2 doit être suffisante pour, partant de E, amener l’atome A à l’ionisation E+, c’est-à-dire lui apporter une énergie suffisante pour arracher un électron. L’atome E devient alors l’ion E+, dont la charge électrique permet de l’entraîner hors du mélange par un champ électrique approprié.
Il faut, par contre, que les photons d’énergie h 益2 ne puissent amener l’atome F ni à l’excitation (donc 益2 益1) ni, directement, à l’ionisation ( 益2 麗 益3). Pour certains atomes, 益2 peut être égal à 益1 et un laser unique suffit.
La photoionisation est utilisée pour la séparation de l’uranium. Elle met en œuvre un four où est vaporisé l’uranium (car le processus, pour permettre la pénétration de la lumière, doit se dérouler en milieu gazeux).
La photodissociation
On s’intéresse cette fois à des molécules. On peut exciter ainsi, comme on le faisait pour l’atome isolé, la molécule comportant un isotope spécifique. Ensuite, l’action d’un second laser, d’énergie appropriée, sur la molécule excitée l’amène à la dissociation. L’atome recherché est alors piégé par voie chimique.
On peut également, par cette méthode, séparer 235U de 238U par irradiation d’UFi6, qui se décompose en U5 + F.
Dans l’ensemble, la séparation isotopique par laser est une méthode intéressante par son rendement relativement élevé, qui conduirait, par exemple, à un coût moitié moindre de celui de la diffusion gazeuse.
La fusion nucléaire par laser
Le laser, s’il constitue la source lumineuse la plus monochromatique que l’homme sache réaliser, s’il est également, à l’inverse, capable d’émettre les signaux les plus brefs connus, est encore capable d’une autre performance: sa cohérence, qui autorise la focalisation du faisceau dans un volume très petit (de l’ordre de3), permet au laser de donner naissance à de considérables concentrations d’énergie. Si cette propriété était déjà largement mise à profit – avec des lasers continus ou impulsionnels – pour l’usinage des matériaux, l’utilisation comme source de très puissants lasers déclenchés conduit à des densités de puissances comparables à celles qui règnent au sein des explosions nucléaires (cf. énergie THERMONUCLÉAIRE).
On a alors montré que, inversement, le «chauffage» par laser d’un mélange de deutérium D et de tritium T devrait permettre d’amorcer la réaction nucléaire :

Dans cette voie, l’intérêt du laser est double. Outre la puissance considérable qu’il peut apporter au combustible: D + T, communiquant ainsi aux atomes de D et T la température (c’est-à-dire les vitesses d’agitation thermique) nécessaire pour permettre aux noyaux – malgré leur répulsion électrostatique mutuelle – d’entrer en contact pour fusionner, il apporte cette puissance en un temps tellement bref que la réaction thermonucléaire peut se développer avant que – précisément du fait de leur agitation – les atomes chauffés se dispersent, arrêtant ainsi la réaction. La rapidité du chauffage est donc telle que les atomes chauffés n’ont pas le temps de se disperser: on peut dire ainsi que seule leur inertie les retient, et, pour cette raison, cette méthode est appelée «la fusion par confinement inertiel».
De nombreux pays consacrent des efforts importants pour montrer la faisabilité de la fusion par confinement inertiel, mettant en œuvre des lasers de plus en plus puissants, d’abord pour atteindre le seuil d’amorçage de la réaction, puis pour améliorer le rendement du processus de fusion. En effet, les perspectives entrevues sont immenses, puisque le deutérium est abondant dans l’eau de mer, tandis que le tritium nécessaire pourrait assez facilement être fabriqué par une réaction auxiliaire sur du lithium. Dans ces conditions, une source quasi inépuisable d’énergie deviendrait, pour la première fois de son histoire, accessible à l’homme.
Plusieurs types de lasers se disputent la faveur des scientifiques.
Les sources les plus puissantes, à l’heure actuelle, sont des chaînes (ainsi nomme-t-on un oscillateur suivi de nombreux amplificateurs) à verre au néodyme, suivies de cristaux tripleurs de fréquence, car l’efficacité du rayonnement est bien plus grande à 0,35 mm. On peut citer: Nova, au laboratoire de Livermore (États-Unis), qui engendre 70 kJ à 0,35 mm, en quelques 10 size=1漣9 s; Gekko XII, à 牢saka (Japon), engendrant 15 kJ à 0,35 mm, en 10 size=1漣9 s; Phebus, à Limeil (France), avec 14 kJ en 2,5 憐 10 size=1漣9 s.
Une nouvelle génération de lasers ultrapuissants se prépare aux États-Unis et en France. La décision officielle n’est pas encore prise, mais les études et les premières réalisations sont déjà très avancées. Le projet américain s’appelle Nova Upgrade, et les caractéristiques sont impressionnantes; en effet, les énergies par impulsion de 3 à 5 nanosecondes de durée atteindront de 1,5 à 2 mégajoules à une longueur d’onde de 351 nanomètres. Cela correspondra à des puissances crêtes de 300 à 600 térawatts (de 3 à 6 憐 1014 W). Ces systèmes ne comportent plus les mêmes formes d’amplificateurs (barreaux ou disques comme dans l’actuel laser Nova); ils auront une structure en 18 faisceaux avec chacun 16 amplificateurs à solides segmentés (288 faisceaux lasers en tout).
3. Applications des lasers en biologie et en médecine
L’apparition en 1960 du laser a permis aux médecins et aux biologistes de réaliser des expériences nombreuses. Une description détaillée des propriétés physiques de cette source de lumière ayant été exposée plus haut, on se limitera au rappel de la caractéristique fondamentale d’un laser: c’est une source de rayonnement qui présente une grande cohérence temporelle et spatiale. La cohérence spatiale permet d’obtenir, par focalisation du faisceau laser, des densités de puissance énormes, car l’énergie lumineuse peut être concentrée dans un petit volume déterminé à la limite par les lois de la diffraction (fig. 20). Dans le cas des lasers déclenchés, cette énergie est en outre délivrée dans des temps très courts (de l’ordre de la nanoseconde et de la picoseconde). Cette propriété, surtout, a reçu des applications en médecine et en biologie.
Aspects physiques de l’interaction rayonnement laser-matériel biologique
L’absorption de la lumière visible par les êtres vivants est liée à l’excitation des pigments, c’est-à-dire des molécules chromophores qui existent dans certaines cellules. Ces molécules reviennent à leur état initial de plusieurs façons: thermalisation de l’énergie absorbée; fluorescence ou phosphorescence, c’est-à-dire émission d’une lumière de longueur d’onde supérieure à celle de la lumière incidente; transformations chimiques.
D’un point de vue macroscopique, les quatre principaux effets de l’action du laser sur du matériel biologique sont les suivants :
– On observe d’abord une action photochimique qui, tout au moins pour des densités de puissance modérées, ne se distingue pas de celle obtenue avec une source classique, comme l’a montré une série d’expériences d’irradiation dans l’ultraviolet de cellules en culture de tissus. Mais, pour des densités de puissance plus grandes, à la longueur d’onde 694,3 nm, il a été mis en évidence une absorption à deux photons par la molécule de nicotinamide adénine dinucléotide (NADH).
– Pour des énergies importantes, il peut y avoir évaporation d’une partie du matériel biologique. Dans certains cas (densités de puissance supérieures à 1010 W/cm2), il se produit une ionisation du matériel, et la température peut atteindre plusieurs dizaines d’électrons-volts (1 eV correspond à environ 104 K). Il se crée un plasma lumineux transitoire qui permet d’analyser spectroscopiquement la composition qualitative d’échantillons de la substance irradiée.
– Pour des énergies plus modérées, les principaux effets sont dus à l’action thermochimique et à la dégradation thermique des matériaux. Des études pratiques et théoriques tenant compte de la diffusion thermique permettent de prévoir le volume de la région lésée.
– Enfin, des effets acoustiques peuvent accompagner l’action du laser. Ces derniers sont dus principalement à la dilatation rapide des matériaux après absorption de l’énergie du laser.
C’est le troisième effet qui a reçu le plus grand nombre d’applications. Il est difficile de faire une classification parmi les travaux souvent très divers. On indiquera, donc, d’une manière non limitative, les résultats les plus marquants en biologie et en médecine, et on essayera de montrer la spécificité du laser pour de tels usages.
Le laser en médecine
On a introduit le laser dans les diverses disciplines médicales, telles la chirurgie, l’ophtalmologie, la cancérologie, la stomatologie, l’urologie et la cardiologie; il peut être utilisé pour le diagnostic ou bien en thérapeutique.
Le laser en chirurgie
Un laser continu peut servir comme une sorte de scalpel lumineux incisant les tissus par brûlure. Les facteurs dont dépend l’action obtenue sont: l’absorption et la réflexion du flux lumineux par les tissus à la longueur d’onde du laser; la densité de puissance du laser; la vitesse d’incision; le degré d’irrigation vasculaire; le degré de tension du tissu dans la zone incisée.
Pratiquement, on utilise à cet effet les lasers à gaz carbonique, émettant dans l’infrarouge (10,6 猪m). Leur puissance est de 5 à 50 W, et le faisceau est focalisé sur environ 1 mm2. Pour des incisions cutanées, la vitesse de coupe est d’environ 3 cm/s et l’échauffement des régions voisines n’est pas gênant. La vitesse de cicatrisation est plus lente avec ce nouveau scalpel dont l’avantage principal est d’être hémostatique et capable de coaguler des vaisseaux de 1 mm de diamètre, d’où son usage en chirurgie du foie.
L’introduction de ce scalpel en microchirurgie nécessite de réduire le diamètre du spot jusqu’à quelques dizaines de microns. On est donc obligé de matérialiser ce faisceau à l’aide d’un autre laser continu émettant dans le visible, et la manipulation doit être effectuée sous microscope.
Le laser en ophtalmologie
Les photocoagulateurs utilisés en cas de décollement ou de déchirement de la rétine étaient équipés de lampes au xénon, remplacées maintenant par un laser à argon ou à diode.
Les avantages respectifs de ces sources lumineuses ont été souvent discutés. Si l’on considère que le meilleur résultat est acquis à l’appareil qui utilise le moins d’énergie pour faire une lésion soudant la rétine à la choroïde, l’avantage va au laser déclenché; en effet, grâce à la brièveté de l’irradiation (30 ns), il faut dix fois moins d’énergie, et les lésions sont plus petites. Un inconvénient à l’emploi de ce type de laser est la vague de pression qui accompagne son action. Des pressions transitoires de l’ordre de quelques dizaines d’atmosphères peuvent être rencontrées au voisinage de la zone traitée et être la cause d’hémorragies. Néanmoins, cet inconvénient s’estompe en employant un laser relaxé, c’est-à-dire présentant des trains d’impulsions durant environ une milliseconde, et des statistiques portant sur plusieurs centaines de cas montrent un taux de guérison de 90 p. 100.
Le laser en cancérologie
L’utilisation du laser pour le traitement de certaines tumeurs malignes avait fait naître bien des espoirs. Les résultats obtenus sont variés et discutés. Le laser ne peut reconnaître les cellules malades que si ces dernières présentent une absorption plus grande que les cellules saines. C’est pour cette raison que l’on s’est intéressé au traitement des mélanomes (tumeurs mélaniques ou à pigments): après une irradiation avec une énergie de 1 500 à 1 700 J/cm2, la tumeur se nécrose et laisse place à une cicatrice aspécifique. Mais l’existence dans les tumeurs de nombreuses cellules achromiques et le fait que le rayonnement du laser n’atteint pas les cellules qui se trouvent en profondeur expliquent que pour le moment le laser ne constitue pas un outil dans le traitement des cancers; par contre, il est employé pour effacer les tatouages et les «taches de vin».
Le laser en biologie
L’étude de la fonction d’un organe, une glande par exemple, implique une destruction totale ou partielle de cet organe; le physiologiste peut alors observer sur l’animal les effets de l’ablation. En revanche, cette technique n’est pas applicable à la détermination des fonctions des organites cellulaires qui sont trop petits (un à deux microns) pour être extirpés ou lésés à l’aide des micro-outils même les plus fins [cf. MICROCHIRURGIE]. La découverte du laser a donc fourni au cytologiste, en particulier, un outil qui vient s’ajouter à l’ultra-centrifugation, au microscope électronique et aux traceurs.
Les effets observés après irradiation de cellules en culture de tissus ont été reliés à l’absorption spécifique de différents constituants cellulaires. Ainsi, la respiration cellulaire est perturbée après irradiation à 530 nm à l’aide d’un laser déclenché. Une diminution de la consommation d’oxygène serait due à la désorganisation de la chaîne des transporteurs d’électrons des mitochondries après absorption d’énergie par les cytochromes.
Une autre application du laser à la biologie est son introduction dans le domaine de la micro-irradiation. Dès 1962, un premier essai de micro-irradiation, en remplaçant la source classique par un laser à rubis (longueur d’onde 694,3 nm), fut effectué sur des globules rouges riches en hémoglobine, qui absorbe fortement dans le bleu (bande de Soret). Malgré la très faible absorption du matériel biologique pour cette longueur d’onde, de petits coagula se formaient à l’endroit du spot d’irradiation.
Cette expérience servit de point de départ à des essais de microchirurgie au niveau cellulaire. Toutefois, comme les cellules animales, qui ne possèdent pas de pigments naturels particuliers, tels l’hémoglobine ou les cytochromes, n’absorbent pas dans le domaine visible, mais fortement dans l’ultraviolet, il est nécessaire de remplacer ces pigments par des colorants vitaux (vert Janus, acridine orange), susceptibles de se fixer sur telle ou telle catégorie d’organites. Ces colorants, employés à des concentrations très faibles, ne sont pas, ou sont peu toxiques pour la cellule, et à ces concentrations la spécificité de leur site de fixation est accrue. Après cette « infracoloration», on se trouve donc en présence d’une cellule dont une catégorie d’organites présente une très faible absorption dans une bande généralement assez large du spectre visible. Ainsi, grâce aux fortes densités de puissance réalisées en focalisant un faisceau laser, il devient théoriquement possible de détruire sélectivement une catégorie d’organites. La constante de relaxation thermique (c’est-à-dire le temps de retour à l’équilibre thermique), liée à un organite ayant un volume de quelques 猪m3 ou moins, est très petite, et l’on est généralement conduit à utiliser des lasers déclenchés afin de pouvoir faire absorber à la cellule une énergie suffisante dans un temps très bref.
Cette technique de microchirurgie a pu être appliquée à différentes catégories d’organites telles que les mitochondries, les lysosomes, les nucléoles ou les chromosomes. Ainsi, des travaux ont été faits sur l’activité enzymatique après irradiation des mitochondries (fig. 21); de même, l’irradiation des gènes organisateurs du nucléole permet d’étudier la modification du nombre et de la taille de cet organite.
En embryologie, enfin, il a été possible de détruire sélectivement différentes parties de l’œuf afin d’étudier le rôle de chaque zone dans l’embryogenèse.
Danger présenté par l’emploi des lasers
Il est préférable d’éviter d’exposer la peau à l’action du laser. Dans le domaine visible, il semble que la seule action du laser soit thermique. Ainsi, un laser à rubis déclenché d’une énergie de 1 J provoque un érythème pendant quelques heures. Le plus grand danger est une illumination intempestive de l’œil. Le tableau 2 donne les doses tolérables adoptées par l’armée américaine. Ces doses peuvent paraître très faibles à la plupart des expérimentateurs, mais en réalité ces derniers ne prennent que des précautions insuffisantes.
4. L’arme laser
La possibilité d’infliger quasi instantanément et à grande distance des dommages à un objectif ennemi a toujours excité l’imagination. L’idée d’utiliser à cette fin un faisceau de lumière concentrée remonte au IIe siècle avant J.-C., puisqu’on attribue à Archimède la paternité de la première arme à énergie dirigée, constituée de miroirs focalisant la lumière solaire sur les voiles des nefs romaines, lors du siège de Syracuse, afin de les incendier et de semer l’effroi chez l’ennemi par l’emploi d’une arme précise et silencieuse. Ce concept, popularisé par les auteurs de science-fiction sous le terme de «rayon de la mort», est revenu occuper le devant de la scène dès 1961, date de l’invention du laser.
En effet, les propriétés spécifiques du rayonnement laser (directivité, monochromaticité) ont rapidement conduit à envisager l’emploi du laser en tant qu’arme ou constituant de cette dernière. Les programmes de recherche sur les armes laser tactiques et stratégiques se sont alors succédé dans la plupart des grands pays industrialisés, en particulier aux États-Unis, où certains de ces programmes ont été fédérés dans le cadre du projet d’Initiative de défense stratégique (I.D.S.), proposé par le président Ronald Reagan dans son discours désormais célèbre du 23 mars 1983. Ce projet, qui vise à établir un bouclier de défense spatiale contre les missiles stratégiques, repose sur l’emploi d’armes à énergie dirigée, parmi lesquelles les lasers jouent un rôle important. Mais les niveaux de puissance et d’énergie requis et les nombreuses difficultés technologiques à surmonter en font encore, à de rares exceptions près, des armes du futur.
Effets des lasers sur les matériaux
Les effets particuliers des lasers sur la matière sont dus à la forte densité énergétique spectrale du rayonnement cohérent. Ils dépendent de la longueur d’onde laser, de la nature des matériaux irradiés et de l’état hydrodynamique de l’air ambiant. Il est possible de distinguer deux catégories d’effets, selon le mode d’application de l’éclairement; les lasers dits continus (durée d’émission comprise entre 0,1 s et quelques dizaines de secondes) produisent des effets purement thermiques dus à l’absorption du rayonnement par les matériaux. Le chauffage résultant conduit à la fusion, puis à la vaporisation des métaux et à la délamination des matériaux composites, donc à leur rupture. Les lasers impulsionnels (délivrant des puissances élevées – de 106 à 1012 watts – pendant des temps très courts – de 1 à 10 猪s) induisent, en amont des cibles, des phénomènes hydrodynamiques très violents (détente de plasma, vaporisation brutale) qui leur communiquent une impulsion mécanique susceptible de les endommager. De ces effets dépendront les possibilités d’utilisation des armes laser dans les domaines tactique et stratégique.
Armes laser tactiques
L’arme laser tactique serait déployée sur le champ de bataille terrestre, aérien ou maritime. Sur le premier d’entre eux, une arme laser embarquée sur char est capable d’assurer la protection d’autres blindés contre des missiles antichars air-sol. À titre d’exemple, des lasers C2 ou DF, dont les longueurs d’onde respectives de 10,6 et 3,8 猪m se propagent bien dans l’atmosphère, émettant 1 MW pendant une dizaine de secondes, détiennent la possibilité d’assurer la neutralisation des missiles air-sol, soit par une destruction pure et simple, soit par aveuglement de l’autodirecteur infrarouge. Dans ces sources, l’effet laser est obtenu par réaction chimique, ce qui facilite l’emport sur un véhicule (réserves de gaz). De la même manière, un laser chimique DF peut être embarqué sur un navire, afin d’assurer la protection d’un porte-avions contre des missiles mer-mer du type Exocet. Dans ce dernier cas, le problème de la compactisation du système est moins critique que pour une arme laser sur char.
La défense au sol de bases aériennes contre les attaques par missiles air-sol paraît plus facilement réalisable, dans la mesure où le déploiement de la source laser est peu limité par l’espace disponible, et où il est possible d’imaginer une défense étendue aux attaques des avions ou des hélicoptères. Les limitations de telles armes sont liées au pointage, à la propagation atmosphérique et aux temps d’engagement des cibles. Pour produire une action destructive, le faisceau de l’arme laser doit être focalisé à grande distance à travers l’atmosphère sur une cible en mouvement rapide (jusqu’à Mach 2) au moyen d’une optique de grande dimension capable non seulement de faire varier la position de son foyer, mais également de maintenir la tache sur la cible avec une précision de l’ordre de 10 microradians, en corrigeant simultanément les écarts dus à la turbulence de l’air et à la défocalisation liée au chauffage du trajet optique par le faisceau lui-même. À de tels niveaux de puissance, la faible part d’énergie absorbée par l’air ambiant est suffisante pour l’échauffer au point de modifier son indice de réfraction, et créer ainsi une pseudo-lentille divergente qui annule l’effet de la focalisation. Ces perturbations sont corrigées au moyen d’optiques déformables qui délivrent au miroir de focalisation un front d’onde dont les écarts de phase, évalués par l’analyse du retour thermique de la cible, minimisent les inconvénients décrits ci-dessus. Cette méthode reste efficace tant que la fréquence des turbulences ne dépasse pas 100 Hz. Aux États-Unis, une source laser C2 de 400 kW embarquée, sur un avion de type K.C. 135 et associée à un tel système optique, a abattu en vol six missiles air-air Sidewinder, en 1983, tandis que, le 23 février 1989, le laser DF Miracl a détruit en vol, pour la première fois, un missile tactique supersonique.
L’emploi tactique des lasers impulsionnels (ou impulsionnels répétitifs) est actuellement peu envisagé. En effet, les très fortes intensités émises (jusqu’à 1010 W/cm2) provoquent rapidement la formation d’un plasma absorbant sur les aérosols en suspension dans l’air, empêchant ainsi le dépôt d’énergie sur les cibles. Cependant, certains scénarios particuliers (brouillage d’autodirecteurs) restent compatibles avec l’emploi de lasers impulsionnels, dans la mesure où ces applications ne nécessitent que des flux laser inférieurs au seuil de formation du plasma (de l’ordre de 5 . 106 W/cm2 à 10,6 猪m).
Armes laser stratégiques
L’intégration de lasers dans un système de défense contre des missiles stratégiques implique un déploiement d’armes dans l’espace (fig. 22). En effet, ces missiles, lancés du sol ou à partir de sous-marins, effectuent la majeure partie de leur trajectoire à très haute altitude et doivent donc être attaqués pendant leur phase propulsée, lorsqu’ils sont vulnérables et détectables. On peut envisager, par exemple, de les engager depuis l’espace au moyen de stations porteuses de lasers chimiques continus HF (action thermique, puissance requise de l’ordre de 50 MW) ou impulsionnels excimères (effets mécaniques sur les structures, énergie comprise entre 10 et 100 MJ). Dans le cadre du programme I.D.S., les États-Unis ont développé un laser chimique HF de 5 MW (Alpha), destiné à être satellisé avant 1995 pour constituer la première démonstration d’une arme laser spatiale. Certains scénarios prévoient le déploiement de stations au sol, comprenant des lasers excimères ou à électrons libres, dont le faisceau serait relayé par des miroirs placés en orbite géostationnaire vers les «miroirs de combat» en orbite basse, avant d’être focalisé sur les cibles.
Des projets plus futuristes prévoient l’emploi de lasers à rayons X pompés par explosion nucléaire et lancés au moment de l’attaque («pop-up»).
Ces deux concepts impliquent de toute façon des contraintes sévères de pointage à longue distance (à 5 000 km, la précision requise est de 10 nanoradians) sur des cibles se déplaçant à la vitesse angulaire de quelques milliradians par seconde. Par ailleurs, les problèmes d’évacuation de chaleur dans le vide spatial et de compactisation des sources d’énergie sont loin d’être résolus, ce qui milite en faveur des armes laser au sol. En particulier, les concepts d’arme laser antisatellite (A.S.A.T.) semblent prometteurs, les seuils de dommage des satellites étant plus bas que ceux des missiles balistiques, généralement durcis aux agressions électromagnétiques (fig. 23).
Encyclopédie Universelle. 2012.