CINÉMATIQUE
La cinématique est la théorie qui, à l’intérieur de la mécanique, a pour objet la description des mouvements des systèmes matériels.
Deux notions sont absolument indispensables à l’élaboration de la cinématique sous sa forme classique: celle de solide invariable et celle de temps. Muni d’un espace euclidien dans lequel il peut mesurer des longueurs et situer des points géométriques et des solides, muni d’un dispositif chronométrique à l’aide duquel il peut mesurer des durées de manière continue et affecter une date à tout événement instantané, le mécanicien se livre alors à la description des mouvements des systèmes physiques en commençant par le plus simple de ces systèmes, celui qui est constitué d’un seul solide.
Étudier, par rapport à un repère (R) = (O, ゑ, を, ん), le mouvement d’un solide (S) c’est étudier le mouvement, par rapport à (R), de n’importe quel point MS lié à (S), ce qui donne toute son importance à la cinématique du point lié à un solide : il s’agit, en somme, de savoir où se trouve tel point à un instant quelconque, s’il y passe vite et si, ensuite, il ira plus ou moins vite; c’est pourquoi on caractérise le mouvement d’un point MS par rapport au repère (R) en étudiant les variations du vecteur de situation de MS dans (R), soit OMS 轢, en fonction de la variable de temps t correspondant au dispositif chronométrique utilisé. Cette étude conduit à définir les notions de trajectoire , de vecteurs cinématiques du premier ordre (vitesse) et du second ordre (accélération); elle amène à préciser ce qu’on entend par mouvement accéléré , par mouvement décéléré (ou retardé); l’étude du mouvement de MS dans (R) fournit des renseignements sur ces nouvelles notions, bien qu’initialement elle ne consiste qu’en l’étude de OMS= に(t ), fonction vectorielle du temps exprimée par exemple sous la forme x ゑ + y を + z ん, c’est-à-dire à l’aide de ses composantes x, y, z dans la base ( ゑ, を, ん) associée aux directions d’axes de (R).
1. Solide invariable et temps
Solide invariable
La notion abstraite de solide invariable, qui est essentielle pour le repérage, est fondée sur des observations simples.
Si l’on a marqué sur deux objets, S et (constitués de matériaux tels qu’acier, bois ou pierre), deux points, A et B, sur S et deux points, 見 et 廓, sur , et si les formes de ces deux objets permettent de réaliser les coïncidences de A avec 見 et de 隣 avec 廓, alors il apparaît que:
– dans tout déplacement de par rapport à S respectant ces deux coïncidences, il existe sur S une infinité de points C1, ..., Ci , ..., Cn , que l’on peut marquer, et il existe sur une infinité de points 塚1, ..., 塚i , ..., 塚n , que l’on peut également marquer et qui restent en coïncidence géométrique chacun à chacun (C1 avec 塚1, ..., Ci avec 塚i , ..., Cn avec 塚n ); les points Ci constituent la droite AB; les points 塚i constituent la droite 見廓 (exemple: déplacement d’une porte par rapport à un mur S);
– si l’on oriente les droites AB et 見廓 dans le sens de A vers B et de 見 vers 廓, la coïncidence de A et 見 et la coïncidence des axes définis par ces orientations entraînent les coïncidences de B et 廓, ..., de Ci et 塚i , etc.;
– si le corps S présente une arête rectiligne AB et le corps une arête rectiligne 見廓, il est possible d’amener ces arêtes rectilignes (ou règles) en coïncidence géométrique d’une infinité de façons, A venant, par exemple, coïncider avec un point arbitraire 塚i de 見廓: il est possible de faire glisser AB sur 見廓, c’est le cas d’une porte que l’on va sortir de ses gonds (fig. 1).
Les solides naturels vérifient approximativement les trois propriétés précédentes. Par idéalisation, le géomètre imagine des solides (dits invariables) qui vérifient rigoureusement ces propriétés et constituent un schéma géométrique utile des solides naturels (c’est en ce sens approximatif que l’on peut considérer l’ensemble de la terre comme un corps solide).
Distance
La distance est une grandeur attachée à tout ensemble de deux points A et B d’un solide invariable; c’est une grandeur mesurable, car on sait définir l’égalité et la somme de deux distances: si l’on peut faire coïncider AB et 見廓, on dit que les distances AB et 見廓 sont égales; si C est un point de la droite AB compris entre A et B, on dit que la distance AB est la somme des distances AC et CB. La mesure d’une distance est alors conditionnée par le choix d’une unité de mesure : l’unité de mesure internationale de distance est le mètre.
D’autre part, si un solide naturel comporte des arêtes constituant un triangle, la somme des mesures de ses angles est approximativement égale à 180 degrés; on postule que c’est une propriété rigoureuse des solides invariables: autrement dit, la géométrie euclidienne, géométrie des solides invariables, rend compte avec beaucoup de précision des propriétés des solides naturels. On peut, dans ce cas, repérer l’espace à l’aide d’un trièdre trirectangle direct (O, ゑ, を, ん) et un espace euclidien se trouve ainsi constitué, dans lequel un point est défini par ses trois coordonnées cartésiennes x, y, z , et la distance de deux points voisins est donnée par l’expression (caractéristique des espaces euclidiens):
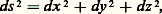
qui est invariante dans tout changement de repère euclidien.
Temps
À la notion de temps se rattachent les notions suivantes: simultanéité, ordre de succession de deux instants, durée de l’intervalle qui les sépare, notions dont la vie courante donne l’intuition.
Si des événements brefs se produisent dans une région limitée de l’espace où se trouvent des observateurs (munis de tous les appareils utiles), chacun de ces observateurs sait dire si, quant à lui, en fonction des appareils dont il dispose, ces événements sont simultanés ou si l’un d’eux est antérieur ou postérieur à l’autre (on sait les difficultés qui s’attachent à l’arrivée d’une course particulièrement serrée). À la limite, on dit qu’un événement bref est instantané: par induction, on admet que simultanéité et ordre de succession d’événements instantanés sont indépendants de l’observateur situé au voisinage de l’événement.
Si des phénomènes se produisent dans des régions de l’espace éloignées les unes des autres et si les observateurs sont eux-mêmes éloignés tant les uns des autres que des phénomènes qu’ils étudient, l’expérience montre immédiatement que ces observateurs ne sont pas en mesure d’estimer la simultanéité de deux phénomènes d’après la simultanéité des sensations que ceux-ci provoquent en chacun d’eux. Par exemple, le phénomène lumineux et le phénomène acoustique accompagnant un coup de canon sont estimés simultanés par un observateur situé au voisinage immédiat du point de tir, tandis qu’un observateur éloigné estimera a priori le phénomène lumineux antérieur au phénomène acoustique, puisque la sensation lumineuse qu’il perçoit est antérieure à la sensation acoustique. Il en est de même si les phénomènes observés se passent en des lieux différents. On parvient toutefois a posteriori à mettre tous les observateurs d’accord sur la simultanéité ou l’ordre de succession de deux phénomènes, et ces notions recouvrent un caractère intrinsèque.
Durée
En ce qui concerne la durée, l’expérience suggère la possibilité de faire correspondre, à tout intervalle qui sépare deux instants, un nombre tel que, à la durée de deux phénomènes identiques (par exemple, oscillation d’un pendule à partir d’une même amplitude), corresponde le même nombre et, à l’ensemble de deux intervalles consécutifs, corresponde la somme des nombres mesurant la durée de chacun d’eux.
La mesure d’une durée est alors conditionnée par le choix d’une unité de mesure : l’unité internationale de mesure des durées est la seconde.
La manière pratique de mesurer le temps résulte des considérations précédentes: tout phénomène périodique, c’est-à-dire formé par la répétition indéfinie d’un même phénomène peut servir à mesurer le temps, avec une approximation d’autant plus serrée que la période du phénomène est plus courte (on rapporte utilement les durées à la période d’une vibration lumineuse). À la limite et par suite des simplifications qu’apporte le calcul différentiel aux études analytiques effectives, on confère à la variable de temps t la propriété d’être continue.
À l’aide des concepts qu’il vient de définir et de préciser, le mécanicien va pouvoir décrire les mouvements, objet de la cinématique.
2. Cinématique d’un point lié à un solide
Cinématique d’un point
On dit qu’un repère (T) et un solide (S) sont liés l’un à l’autre si tout point de (S) a des coordonnées constantes dans (T); on démontre aisément que la condition nécessaire et suffisante pour qu’il en soit ainsi est que trois points non alignés de (S) aient des coordonnées constantes dans (T), c’est-à-dire indépendantes de la valeur numérique prise par la variable de temps.
Il est possible de lier à (S) une infinité de repères; soit (TS) l’un d’entre eux, trirectangle direct, d’origine S et dont ゑs, をs, んs sont les vecteurs unitaires des axes:

on désigne avec un indice inférieur tout élément géométrique lié à (S): point MS, droite S, plan 神S; on dit, par exemple, qu’un point géométrique MS est lié à (S) si ses coordonnées sont des constantes dans un repère (TS). Il arrive souvent que, par souci de simplification d’écriture, on désigne par (S) un repère lié au solide (S).
Parmi tous les repères (S), on n’en fait souvent intervenir qu’un seul dans les raisonnements: il est choisi à cause des simplifications qu’il apporte dans l’étude du mouvement du solide; celle-ci comporte l’étude du mouvement de chacun des points (MS étant l’un d’entre eux) qui sont liés à ce solide.
À la date t , MS coïncide avec le point P(t ) fixe dans (R): P(t ) est appelé position de MS à la date t dans (R).
Trajectoire, vitesse et accélération
On appelle trajectoire de MS dans le repère (R), l’ensemble des points fixes de (R) avec lesquels le point MS vient en coïncidence dans la succession des événements, ou encore l’ensemble des positions de MS dans (R). On désigne cette trajectoire par 臨(R)(MS) pour marquer qu’elle dépend de MS et de (R): par exemple, tel point qui admet relativement à un wagon une trajectoire rectiligne peut admettre une trajectoire parabolique par rapport au sol sur lequel se déplace le wagon. Quand on ne considère qu’un seul repère et un seul point, on peut désigner la trajectoire par 臨, puisque cette notation simplifiée n’introduit aucune ambiguïté.
On appelle vitesse de MS dans le repère (R) le vecteur dérivé par rapport au temps, dans le repère (R), du vecteur de situation OMS= に(t ); on note ce vecteur vitesse (R)(MS):

si aucune confusion ne peut s’introduire.
On appelle accélération de MS dans le repère (R) le vecteur dérivé par rapport au temps, dans le repère (R), du vecteur vitesse (R)(MS); on note ce vecteur accélération ど(R)(MS):

Si aucune confusion ne peut s’introduire, on simplifie la notation:

Ces deux vecteurs cinématiques s’expriment par:
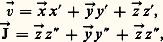
si l’on fait intervenir les vecteurs unitaires liés à (R); x et x sont les deux premières dérivées de x par rapport au temps.
Il est possible toutefois de les exprimer en utilisant des représentations géométriques beaucoup plus générales que la représentation cartésienne: par exemple, la représentation cylindro-polaire (fig. 2).
Dans la pratique, un usage fréquent exprime ces vecteurs selon la trajectoire et «perpendiculairement» à la trajectoire, ce qui se traduit dans la technique du calcul par l’intervention de leurs composantes sur un vecteur unitaire tangent ゝ et sur le vecteur unitaire 益 normal principal en P(t ), à la trajectoire 臨 orientée par ゝ et sur laquelle est définie l’abscisse curviligne s = P(0)P(t ); 益 倫 désigne le bipoint d’origine P(t ) et d’extrémité C(t ), centre de courbure de 臨 en P(t ) (fig. 3). Le vecteur ど 精 = s ゝ est dit accélération tangentielle ; le vecteur ど size=1益 = (s 2/ 倫) 益 est dit accélération normale (fig. 3). Cette façon d’écrire présente un intérêt tout particulier dans le cas d’une trajectoire rectiligne où et ど s’expriment très simplement par les relations: = s ゝ et ど = s ゝ. Dans le cas d’une trajectoire circulaire, l’on pose s = 倫 見 et l’on trouve:

Quelles que soient les représentations utilisées, l’intensité et les composantes du vecteur vitesse ont des mesures qui s’expriment en mètre par seconde: l’unité de vitesse est le mètre par seconde (m . s-1) et la dimension physique d’une vitesse est L-1. L’intensité et les composantes du vecteur accélération ont des mesures qui s’expriment en mètre par seconde par seconde: l’unité d’accélération est le mètre par carré de seconde (m . s-2); et la dimension physique d’une accélération est L-2.
Cas pratiques
Ainsi, jusqu’à l’apparition des chemins de fer, les moyens de locomotion utilisés par l’homme lui permettaient d’atteindre une vitesse de l’ordre de 10 m . s-1 (c’est actuellement la vitesse moyenne du coureur à pied le plus rapide); puis, en un peu plus d’un siècle, les vitesses des transports ont considérablement augmenté: au cours de la Seconde Guerre mondiale, les avions ont atteint en piqué 200 m . s-1, ce qui est inférieur à la vitesse de croisière d’un Airbus (270 m 練 s-1); un quart de siècle plus tard, on voit des hommes se mouvoir à 11 000 m . s-1 au cours des expériences Apollo, ce qui, en moins d’une génération, représente une multiplication de la vitesse par un facteur supérieur à 50.
En ce qui concerne les accélérations, l’homme est soumis au champ de la pesanteur (attraction terrestre), qui lui confère une accélération voisine de 10 m . s-2 (en fait g = 9,81 m . s-2 à Paris); cela signifie que, dans ce champ naturel, la vitesse s’accroît à chaque seconde de 10 m . s-1. Pour qu’une automobile partant du repos effectue, par suite d’une accélération constante, un premier kilomètre en 30 secondes, il faut que son accélération soit de l’ordre de 2,2 m . s-2. Au cours d’une opération de catapultage d’un avion à partir d’un porte-avions, l’accélération du mouvement est de l’ordre de 4 à 5 g (40 à 50 m . s-2). Pour un avion volant à mach 2, qui effectue un virage de 600 mètres de rayon, l’accélération (normale) atteint 6 g , et pour éviter qu’une telle accélération ne provoque des troubles dans l’organisme du pilote, celui-ci est soumis à un entraînement spécial.
Reprenant le langage courant, on dit en cinématique que le mouvement de MS est accéléré (ou, à l’inverse, décéléré) si l’intensité du vecteur vitesse (MS) est croissante (ou, à l’inverse, décroissante); le mouvement de MS est uniforme si l’intensité de son vecteur vitesse reste constante: dans un mouvement rectiligne uniforme, l’accélération est nulle; dans un mouvement curviligne uniforme, l’accélération est normale à la trajectoire.
3. Cinématique du solide
Étudier le mouvement d’un solide, c’est être en mesure d’indiquer la trajectoire, la vitesse et l’accélération de tous les points qui lui sont liés. Le premier de ces trois objectifs n’admet pas de réponse générale: sauf cas particuliers, les trajectoires des différents points liés à un solide n’ont aucun rapport simple; ainsi, dans le mouvement «en ligne droite» d’une bicyclette, un point lié à un moyeu de roue admet une trajectoire rectiligne par rapport au sol (il est immobile par rapport au cadre), tandis qu’un point de la bande de roulement d’un pneumatique (supposé rigide) admet une trajectoire cycloïdale par rapport au sol (et circulaire par rapport au cadre).
Par contre, dès que sont connues la vitesse et l’accélération d’un point lié au solide, et que la manière dont varie en fonction du temps l’orientation du solide (S) dans le repère (R) est précisée, les vitesses et les accélérations de tous les points liés au solide peuvent être évaluées.
Pour orienter un solide (S) dans un repère (R), on utilise les vecteurs ゑS, をS, んS, et pour étudier les variations de cette orientation en fonction du temps, on étudie les variations des vecteurs ゑS, をS, んS par rapport aux vecteurs ( ゑ, を, ん) de la base du repère (R). Il ne peut se présenter que trois cas:
– ou bien ゑS, をS, んS sont indépendants du temps et l’on dit que le mouvement du solide (S) par rapport au repère (R) est un mouvement de translation ou encore que (S) est en translation par rapport à (R); on peut alors, sans restreindre la généralité du problème, supposer que ゑS = ゑ, をS = を, んS = ん (cas du mouvement d’un tiroir par rapport à une table où il coulisse, ou inversement mouvement de la table par rapport au tiroir); les dérivées ゑ S, を S, ん S sont nulles (fig. 4); – ou bien l’un des trois vecteurs ゑS, をS, んS est indépendant du temps; on peut, sans restreindre la généralité du problème, supposer que んS = ん (cas du mouvement de la Terre par rapport au Soleil); dans ce cas l’orientation angulaire de (S) par rapport à (R) est caractérisée par la fonction:

mesurée sur ん = んS et l’on trouve les résultats indiqués sur la figure 5. 見 est dite vitesse angulaire du mouvement; 見 est dite accélération angulaire du mouvement (en ce qui concerne la Terre, sa vitesse angulaire est de 1 tour par jour, soit environ 7,3 . 10-5 radian par seconde; son accélération angulaire est nulle);
– ou bien les trois vecteurs ゑS, をS, んS dépendent du temps; dans ce cas (mouvement d’une toupie, par exemple) l’orientation angulaire de (S) par rapport à (R) est précisée en général par la donnée de trois angles; on choisit souvent les angles d’Euler ainsi définis: ょ étant un vecteur unitaire (dit nodal) orthogonal à ん et à んS, ces trois angles sont la précession 切 (t ) = ( ゑ, ょ) mesurée sur ん, la nutation (t ) = ( ん, んS) mesurée sur ょ, la rotation propre 﨏 (t ) = ( ょ, ゑS) mesurée sur んS (fig. 6). L’étude des variations de l’orientation d’un solide (S) par rapport à un repère (R) comporte la démonstration du fait que, dans tous les cas, il existe un vecteur ゚RS tel que まS = ゚RS 廬 まS, où まS est l’un des vecteurs unitaires ゑS, をS ou んS; le vecteur ゚ = ゚RS est appelé le taux de rotation du solide (S) dans le repère (R).
Si le solide (S) est en translation par rapport à (R), son taux de rotation est nul; si le mouvement de (S) par rapport à (R) est tel qu’un axe lié à (S) garde une orientation constante dans (R), le taux de rotation ゚RS est égal à 見 ん; si l’orientation angulaire de (S) par rapport à (R) fait intervenir les trois angles d’Euler, le taux de rotation est égal à 切 ん + ょ + 﨏 んS. Dérivant alors par rapport au temps dans le repère (R), l’identité: OM 轢S = OP 轢S + PSMS 轢, il vient:
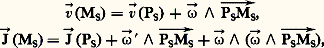
 étant la dérivée du taux de rotation par rapport au temps, soit dans le repère (R), soit dans le repère (S). Les formules ci-dessus définissent les distributions des vitesses et des accélérations des points liés à un solide (S) en mouvement par rapport à un repère (R). On voit qu’elles permettent d’obtenir la vitesse (et l’accélération) de n’importe quel point lié à (S), quand on connaît ゚ (et par dérivation ゚ ), et la vitesse (et l’accélération) d’un point quelconque (observable ou non) lié à (S).
4. Notion de torseur
La notion de torseur est fondamentale en mécanique; elle n’est pas indispensable à un exposé de cinématique, mais, comme elle peut y trouver usage, on donnera ici un aperçu de la théorie des torseurs.
Dans un espace à trois dimensions , un torseur, noté 淪, est défini par un ensemble de deux champs de vecteurs: le premier de ces champs, noté れ 淪, est indépendant du point considéré, et désigné sous le nom de somme géométrique du torseur; le second de ces champs est variable (en général) d’un point à un autre selon la loi de définition :

quels que soient les points P et Q de l’espace; le vecteur ぬP 淪 est appelé moment en P du torseur 淪.
Les vecteurs れ 淪 et ぬP 淪 constituent les éléments de réduction en P du torseur 淪.
On dit que deux torseurs 淪1 et 淪2 sont égaux et on écrit:

s’ils ont mêmes éléments de réduction en un point quelconque Q (on démontre que cette définition est indépendante du point Q).
On dit qu’un torseur 淪 est nul et on le note alors0, si ses éléments de réduction en Q sont nuls (ils sont alors nuls en tout point).
On désigne le torseur «combinaison linéaire» de 淪1 et 淪2 à coefficients scalaires k 1 et k 2 par 淪, ce torseur ayant comme éléments de réduction en P:
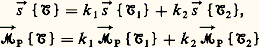
(on démontre que cette définition est indépendante du point P). L’application de cette définition dans certains cas particuliers conduit à définir la somme et la différence ainsi que la multiplication d’un torseur par un scalaire; immédiatement, elle s’étend à un nombre fini de torseurs:

On appelle produit scalaire de 淪1 et de 淪2, que l’on note 淪1 . 淪2 ou 淪2 . 淪1 (car la commutativité est évidente), le nombre réel défini par:

On démontre que ce produit scalaire est indépendant du point P qui intervient dans sa définition.
Si l’on multiplie scalairement chaque membre de l’équation qui constitue la définition des variations du moment d’un torseur par PQet par れ 淪, on obtient:

puis:

Le premier résultat exprime que les mesures algébriques des projections orthogonales des vecteurs ぬP et ぬQ sur un axe de support PQsont égales (propriété dite d’équiprojectivité ): cette mesure est dite moment scalaire du torseur sur l’axe considéré.
Le second résultat exprime que le produit scalaire 溜 des éléments de réduction en un point (pour un torseur donné) est indépendant de ce point: le scalaire 溜 est dit invariant scalaire du torseur considéré.
Ainsi, à un torseur 淪 donné on peut associer le scalaire 溜 et le vecteur れ qui sont deux invariants (indépendants de P). On classe les torseurs à l’aide de ces deux invariants:face="EU Arrow"
れ = ( 溜 = 0 nécessairement), face="EU Arrow" ぬP = : torseur nul ;
れ = ( 溜 = 0), face="EU Arrow" ぬP : torseur-couple de moment ぬ (indépendant de P);
れ , 溜 = 0: torseur-vecteur, pour lequel il existe un alignement de points Q de moment nul (face="EU Arrow" ぬQ = ) défini par:
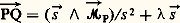
(, scalaire réel);
れ 0, 溜 0: torseur quelconque, pour lequel, en tout point de l’alignement précédemment défini (axe central ), le moment ぬQ est colinéaire à れ : face="EU Arrow" ぬQ = 溜 れ/ れ2.
Cette classification est fondamentale.
5. Torseur distributeur des vitesses
La relation importante concernant, dans un même repère (R), les vecteurs vitesses de deux points MS et PS liés à un solide peut s’écrire:

par conséquent, si on associe au mouvement de (S) dans (R) le torseurRS dont les éléments de réduction en PS sont ゚RS (somme géométrique) et (R)(PS) (moment en PS), alors (R)(MS) sera le moment en MS de ce même torseur appelé torseur distributeur des vitesses de (S) dans (R); ainsi:

et:

Il est évident que l’invariant scalaire du torseur distributeur des vitesses ne peut être nul que si ゚RS = , ou bien si (R)(MS) = , ou bien encore si (R)(MS) est orthogonal à ゚RS.
La classification des torseurs permet d’énumérer les divers mouvements que peut prendre un solide dans un repère.
戀
索RS =0: (S) est immobile par rapport à (R).
戀
索RS est un torseur-couple de moment ぬ: (S) est en translation par rapport à (R), et tout point lié à (S) possède dans (R) une même vitesse ぬ et une même accélération ぬ .
戀
索RS est un torseur-vecteur: il existe alors un alignement de points liés au solide qui, à une date déterminée, ont une vitesse nulle dans (R). Cette circonstance peut se présenter dans deux cas particuliers:
– si (R)(MS) 令 , c’est-à-dire si le solide a au moins un point fixé dans (R) (le solide aura un axe fixé si ゚RS = 見 ん);
– si ゚RS est orthogonal à (R)(MS), c’est-à-dire si le solide (S) est animé d’un mouvement plan sur plan par rapport à (R).
戀
索RS est un torseur quelconque: il existe un alignement de points liés au solide qui, à une date déterminée, ont une vitesse parallèle au taux de rotation; cet alignement porte le nom d’axe instantané de viration .
6. Composition des mouvements
L’étude systématique des relations entre les trajectoires et les vecteurs cinématiques d’un même point M (et notamment d’un même point MS) relativement à deux (ou à plus de deux) repères conduit à la théorie de la composition des mouvements. On considère deux repères mobiles l’un par rapport à l’autre au cours du temps; on connaît donc le vecteur de situation O size=1凞O size=1猪en fonction du temps sur l’une des deux bases () ou ( 猪) et, par exemple, les vecteurs ゑ size=1猪, を size=1猪, ん size=1猪 en fonction du temps sur la base (); cela signifie en particulier que l’on sait dans lequel des trois cas se trouve ( 猪), en ce qui concerne son orientation angulaire par rapport à () (fig. 4, 5, 6) ; ゚ size=1凞猪 est donc évalué. On suppose que le vecteur de situation de M dans ( 猪) est connu en fonction du temps.

où x size=1猪(M), y size=1猪(M) et z size=1猪(M) sont des fonctions connues du temps définissant paramétriquement la trajectoire 臨( size=1猪) (M).
On peut exprimer par exemple:
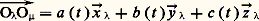
et lier les vecteurs unitaires des deux bases à l’aide du tableau 1; le vecteur de situation O size=1凞Mde M dans () a donc pour expression O size=1凞O size=1猪 size=1轢 + O size=1猪M 轢, c’est-à-dire pour composantes dans () les fonctions du temps:
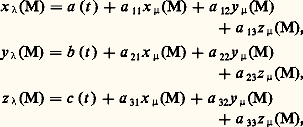
qui définissent paramétriquement la trajectoire 臨( size=1凞)(M). Cette étude montre comment se fait le passage (de manière généralement analytique et compliquée) de la trajectoire de M dans ( 猪) à la trajectoire de M dans ().
On montre immédiatement que si l’on exprime le vecteur に(t ) par ses composantes x size=1猪, y size=1猪, z size=1猪 sur la base ( 猪) et par ses composantes x size=1凞, y size=1凞, z size=1凞 sur la base (), et si l’on pose selon l’usage:

alors:

en particulier, la théorie de composition des vitesses et des accélérations utilise cette formule dans les cas où に = O size=1猪Met に = ( size=1猪) (M).
Pour obtenir la formule dite de composition des vitesses , on dérive, par rapport au temps dans le repère (), chaque membre de l’identité: O size=1凞M= O size=1凞O size=1猪+ O size=1猪M 轢; on obtient, d’après ce qui précède:

Dans cette formule, on distingue alors le groupement:

dans lequel le torseur distributeur des vitesses de ( 猪) dans () est défini par ses éléments de réduction en O size=1猪, savoir: face="EU Arrow" ゚ size=1凞猪 (somme géométrique), () (O size=1猪) (moment).
Ainsi la formule fondamentale de composition des vitesses peut s’écrire utilement sous forme condensée:

Le vecteur 紐M凞猪 est souvent appelé vitesse d’entraînement de M dans le mouvement de ( 猪) par rapport à ().
Pour obtenir la formule dite de composition des accélérations , on dérive par rapport au temps dans le repère () chaque membre de la formule de composition des vitesses; on obtient:
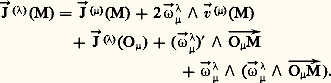
Le vecteur 2 ゚ size=1凞猪 廬 ( 猪)(M) = どC(M size=1凞猪) est souvent appelé accélération de Coriolis de M dans le mouvement de ( 猪) par rapport à (); ce vecteur est nul si le mouvement de ( 猪) par rapport à () est une translation, ou si M est immobile dans ( 猪) ou si ( 猪)(M) est parallèle à ゚ size=1凞猪.
Le vecteur:

est souvent appelé accélération d’entraînement de M dans le mouvement de ( 猪) par rapport à ().
Les formules de composition des vitesses et des accélérations sont utilisées, dans la plupart des cas pratiques, en faisant intervenir plus de deux repères (dans le plus simple des mécanismes, il y a toujours un bâti, une entrée et une sortie d’énergie, ce qui fait au moins trois repères). On démontre par permutation et addition, les formules suivantes:

qui s’étendent à un nombre fini de repères.
De même:
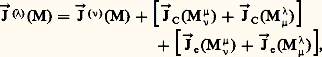
et l’on voit que:
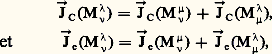
formules qui s’étendent aussi à un nombre fini de repères.
Dans certains raisonnements de cinétique et de dynamique interviennent des repères en translation les uns par rapport aux autres; si ( 猪) est en translation par rapport à (), les formules de composition se simplifient considérablement:

Il est remarquable que la mise en évidence de l’accélération de Coriolis soit contemporaine des progrès accomplis dans les moyens de locomotion: on notera que si ( 猪) est la Terre et () le Soleil, l’accélération de Coriolis de M dans le mouvement de la Terre par rapport au Soleil ne sera notable que si la vitesse ( 猪)(M) de M par rapport à la Terre est assez grande; le terme 2 ゚ size=1凞猪 廬 ( 猪)(M) sera maximum en intensité si ( 猪) (M) est orthogonal à la ligne des pôles terrestres (support du ゚ size=1凞猪), c’est-à-dire si M se déplace d’ouest en est ou d’est en ouest; dans ces conditions, le tableau 2 précise les ordres de grandeur de l’accélération de Coriolis.
7. Cinématique des systèmes de solides
Principes
On vient de voir précédemment que la situation d’un solide (S) dans un repère (R) dépend très généralement de la donnée de six fonctions du temps, à savoir trois coordonnées d’un point lié au solide (S) et trois angles caractérisant l’orientation de (S). On désignera par q size=1見(t ) l’une quelconque de ces six fonctions du temps ( 見 = 1, 2, ..., 6). Dans bien des cas le repère (R) sera lui-même un repère géométrique lié à un solide (R), par conséquent la position d’un solide (S) par rapport à un autre solide (R) dépend très généralement de six paramètres.
On dit qu’on établit une liaison entre (S) et (R) si l’on suppose que les fonctions q size=1見(t ), q size=1見(t ) et t obéissent à l’identité:
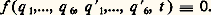
On dit qu’on établit l liaisons (1 諒 l 諒 5) entre (S) et (R) si l’on suppose que q size=1見, q size=1見 et t obéissent aux identités:
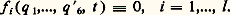
Soit maintenant un ensemble de p solides, considérés dans un ordre arbitraire, mais précisé (par exemple, celui du montage) et supposons que cet ordre soit justement celui des nombres j avec j = 1, 2, ..., p. Tout ce qui a été dit à propos de (S) et (R) en ce qui concerne les liaisons, les trajectoires, les vitesses et les accélérations peut être répété à propos des solides k et k + 1 (où k = 1, ..., p 漣 1). Cette «chaîne» de solides dépend de 6 p paramètres et est soumise à L liaisons (0 諒 L 諒 6 p 漣 1), chacune de ces L liaisons étant réalisée par un système physique convenablement choisi ou par contact entre solides. Dans le cas où la situation de cette chaîne peut être effectivement précisée à l’aide de (6p 漣 L) paramètres indépendants, on dit que la chaîne a (6p 漣 L) degrés de liberté .
Chaînes usuelles de solides
Une sphère (S) reste au contact d’un plan (R) (que l’on prend comme plan Oxy ); le système de ces deux solides est soumis à une liaison: la cote z du centre de la sphère doit être égale au rayon a de la sphère, si l’on suppose que le contact a lieu du côté des cotes positives, et z – a = 0. Cette liaison laisse la possibilité de situer (S) dans (R) par les cinq paramètres indépendants x, y , 祥, , 﨏. Si l’on impose qu’il n’y ait pas de glissement au point de contact M de (S) et de (R), il y a lieu de traduire que ぬMRS= , ce qui introduit deux nouvelles liaisons:

Ces liaisons ne laissent plus la possibilité de situer (S) dans (R) à l’aide de paramètres indépendants choisis parmi x, y , 祥, , 﨏.
Si un solide (S) a un axe fixé par rapport à (R), on peut supposer que OS = O et que んS = ん. Une telle fixation s’appelle un rotoïde ; elle permet de laisser au solide (S) un degré de liberté 見 par rapport à (R). L’axe Ozest appelé axe du rotoïde. Dans une suspension à la Cardan (fig. 7) à trois degrés de liberté, le mouvement du solide (4) par rapport au bâti (1) dépend des valeurs des trois angles d’Euler indépendants l’un par rapport à l’autre, 祥, , 﨏: le solide (2) est lié au bâti (1) par une articulation rotoïde d’axe Oz 轢1 (le solide (2) est l’armature externe du cardan); le solide (3) est lié au solide (2) par une articulation rotoïde d’axe Onorthogonal à Oz 轢1 (le solide (3) est l’armature interne du cardan); enfin le solide (4) est lié au solide (3) par une articulation rotoïde d’axe Oz 轢4 orthogonal à On 轢. Ainsi le solide (4) se trouve avoir un point fixé O dans son mouvement par rapport au bâti (1).
Dans le système bielle-manivelle, on distingue le bâti (1), la manivelle (2), la bielle (3), le piston (4) (fig. 8). La manivelle est liée au bâti par une articulation rotoïde d’axe Oz(perpendiculaire au plan de la figure), la bielle est liée à la manivelle par une articulation rotoïde d’axe Az(son mouvement par rapport au bâti est un mouvement plan sur plan), le piston est lié à la bielle par une articulation rotoïde d’axe Bz(le mouvement du piston par rapport au bâti est un mouvement de translation rectiligne). On peut dire que cette chaîne des trois solides (2), (3), (4) a un degré de liberté 見 par rapport au bâti (1), car on peut exprimer 廓 et x (B) (fig. 8), ce qui permet de formuler (en fonction de 見, 見 , 見 ) les vitesses et accélérations, par rapport à l’un quelconque de ces quatre solides, d’un point lié à un autre quelconque d’entre eux.
cinématique [ sinematik ] n. f.
• 1834; gr. kinêmatikos, de kinêma « mouvement »
♦ Partie de la mécanique qui étudie le mouvement indépendamment des forces qui le produisent. La cinématique du point. Application de la cinématique. ⇒ dynamique.
● cinématique adjectif Relatif au mouvement. ● cinématique (expressions) adjectif Amputation cinématique, amputation pratiquée en vue de la cinématisation. Lacet cinématique, mouvement louvoyant des véhicules ferroviaires. ● cinématique nom féminin Partie de la mécanique qui étudie les mouvements en fonction du temps, sans se préoccuper de leurs causes.
cinématique
adj. et n. f.
d1./d adj. Relatif au mouvement.
d2./d n. f. MECA étude du mouvement des corps indépendamment de ses causes (dont s'occupe la dynamique).
⇒CINÉMATIQUE, adj. et subst. fém.
I.— Adj. Relatif à la cinématique, au mouvement. La viscosité cinématique est le rapport de la viscosité absolue à la densité (J.-J. CHARTROU, Pétroles naturel et artificiels, 1931, p. 19) :
• 1. ... l'état et la composition des populations ne cessent de se modifier. En suivant dans le temps tel aspect particulier, la description statique s'anime et se transforme en une vue cinématique des phénomènes.
Traité de sociol., 1967, p. 277.
Rem. On rencontre ds la docum. l'adj. substantivé : le cinématique « ce qui est en mouvement » :
• 2. En disant que l'altération est un passage du même à l'autre ou une transition d'autre en autre, nous nous laissons derechef égarer (...) par la préséance grammaticale du statique sur le cinématique et du cinématique sur le cinétique, et enfin par une pente invincible à confondre le mouvement se faisant avec le trajet effectué.
JANKÉLÉVITCH, Le Je-ne-sais-quoi et le presque-rien, 1957, p. 26.
II.— Subst. Étude du mouvement des corps, abstraction faite des causes qui le provoquent. On sait le rôle qu'a joué la cinématique des corps solides dans la genèse de la géométrie (H. POINCARÉ, La Valeur de la sc., 1905, p. 242) :
• 3. ... M. Langevin, (...) a montré que les lois de la dynamique peuvent se déduire, à l'aide de l'un des principes fondamentaux de la physique, le principe d'équivalence, du principe de relativité et des lois de la cinématique.
F. PERRIN, La Dynamique relativiste et l'inertie de l'énergie, 1932, p. 11.
SYNT. La cinématique du point, du solide, des fluides; principes de la cinématique; la cinématique classique, relativiste.
— P. ext., plus rare. Mouvement obéissant à des lois :
• 4. Il ne viendrait à personne l'idée de mettre en doute (...) la successive agrégation des particules au sein d'un cristal ou d'une stalagmite; ou la concrescence des faisceaux ligneux autour de l'axe d'une tige. Certaines dispositions géométriques, parfaitement stables à nos yeux, sont la trace et le signe irréfutable d'une cinématique.
TEILHARD DE CHARDIN, Le Phénomène humain, 1955, p. 150.
Prononc. et Orth. :[sinematik]. Ds Ac. 1932. Étymol. et Hist. Av. 1836 subst. cinématique (AMPÈRE, Essai sur la Philosophie des Sciences, 1re part., p. 51 ds Fr. mod., t. 22, p. 42). Formé sur le rad. du gr. 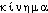 , -
, - « mouvement »; suff. -ique. Fréq. abs. littér. :19.
« mouvement »; suff. -ique. Fréq. abs. littér. :19.
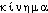 , -
, - « mouvement »; suff. -ique. Fréq. abs. littér. :19.
« mouvement »; suff. -ique. Fréq. abs. littér. :19.DÉR. Cinématiquement, adv. En se référant à la cinématique. Non, il n'y a pas d'espace absolu; ces deux propositions contradictoires :« la terre tourne » et « la terre ne tourne pas » ne sont donc pas cinématiquement plus vraies l'une que l'autre. Affirmer l'une, en niant l'autre, « au sens cinématique », ce serait admettre l'existence de l'espace absolu (H. POINCARÉ, La Valeur de la sc., 1905p. 272). — Seule transcr. ds LITTRÉ : si-né-ma-ti-ke-man. — 1re attest. 1874 (COUSTÉ, Mém. ds Comptes rendus de l'Ac. des sciences, t. 79, p. 1369); de cinématique, suff. -ment2. — Fréq. abs. littér. : 1.
BBG. — GIRAUD (J.). Cinématique. Fr. mod. 1954, t. 22, pp. 42-44.
cinématique [sinematik] n. f. et adj.
❖
♦ Didactique.
1 N. f. Partie de la mécanique qui étudie les mouvements, indépendamment des causes qui les produisent et de la nature des mobiles. ⇒ Mécanique, mouvement. || « On distingue la cinématique du point qui introduit les notions de trajectoire, vitesse et accélération et la cinématique du solide qui s'intéresse à la répartition des vitesses des différents points du solide mobile » (Bouvier et George). || Application de la cinématique. ⇒ Dynamique.
➪ tableau Noms de sciences et d'activités à caractère scientifique.
2 Adj. Relatif au mouvement, à son étude scientifique. || Formule cinématique. || Viscosité cinématique d'un fluide.
0 Disons un mot, à présent, du processus cinématique qu'implique une promenade en forêt. Ce processus est fort simple. Il consiste, dans le chef du promeneur, à opter pour l'une des mille façons de coordonner entre eux, par la marche, les intervalles d'une certaine quantité de troncs contigus (…)
Encyclopédie Universelle. 2012.