Akademik

в теории вероятностей - мера DX отклонения случайной величины Xот ее математич. ожидания , определяемая равенством:

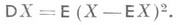(1)

Свойства Д.: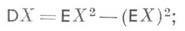

если с - действительное число, то

в частности D(-X)=D(X).

Когда говорят о Д. случайной величины X, всегда предполагают, что существует математич. ожидание 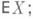при этом Д. DX может существовать (т. е. 'быть конечной) или не существовать (т. е. быть бесконечной). В современной теории вероятностей математич. ожидание случайной величины определяется через интеграл Лебега по пространству элементарных событий. Однако важную роль играют формулы, выражающие математич. ожидание различных функций от случайной величины Xчерез распределение этой случайной величины на множестве действительных чисел (см. Математическое ожидание). Для Д. DX эти формулы имеют вид:

для дискретной случайной величины X, принимающей не более чем счетное число различных значений а; с вероятностями р _i= Р{Х= а _i};

для случайной величины X, имеющей плотность распределения вероятностей р(х);

в общем случае, где F(x)- функция распределения случайной величины Xи интеграл понимается в смысле Лебега - Стилтьеса или Римана - Стилтьеса.

Д. не является единственной мыслимой мерой отклонения случайной величины от ее математич. ожидания. Возможны другие меры отклонения, устроенные по тому же принципу, напр. и т. д., а также меры отклонения, основанные на квантилях. Особая важность Д. объясняется главным образом той ролью, к-рую играет это понятие для предельных теорем. Грубо говоря, оказывается, что если знать математич. ожидание и Д. суммы большого числа случайных величин, то можно полностью определить закон распределения этой суммы: он оказывается нормальным (приблизительно) с соответствующими параметрами (см. Нормальное распределение).

Таким образом, важнейшие свойства Д. связаны с выражением для Д. D(X₁+. . . + Х _п )суммы случайных величин Х ₁, . . ., Х _п:

обозначает ковариацию случайных величин Х _i и X_j. Если случайные величины Х ₁, . . ., Х _п попарно независимы, то cov(X_i, X_j)=0. Поэтому для попарно независимых случайных величин

Обратное утверждение неверно: из (2) не следует независимость. Однако, как правило, применение формулы (2) базируется на независимости случайных величин. Строго говоря, для справедливости (2) достаточно лишь, чтобы cov(X_i, X_j) = 0, т. е. чтобы случайные величины X₁ ,..., Х _п были попарно некоррелированы.

Применения понятия Д. развиваются по следующим двум направлениям. Во-первых, применения в области предельных теорем теории вероятностей. Если последовательность случайных величин Х ₁, Х ₂,. . ., Х _п,. .. обладает тем свойством, что 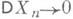при 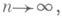то для любого e>0 при

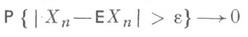
(см. Чебышева неравенство), т. е. практически при больших пслучайная величина Х _n совпадает с неслучайной величиной Е Х _п. Развитие этих соображений приводит к доказательству закона больших чисел (см. Больших чисел закон), к доказательству состоятельности оценок (см. Состоятельная оценка )в математич. статистике, а также к иным применениям, в к-рых устанавливается сходимость по вероятности случайных величин. Другое применение в области предельных теорем связано с понятием нормировки. Нормировка случайной величины Xпроизводится путем вычитания математич. ожидания и деления на среднее квадратичное отклонение иными словами, рассматривается величина Нормировка последовательности случайных величин обычно необходима для получения сходящейся последовательности законов распределения, в частности сходимости к нормальному закону с параметрами 0 и 1. Во-вторых, применение понятия Д. в математич. статистике при обработке выборок. Если смотреть на случайную величину как на реализацию случайного эксперимента, то произвольное изменение шкалы отсчета приведет к преобразованию случайной величины Xв величину Y=sX+a, где а- любое действительное число, s- положительное число. Поэтому часто имеет смысл рассматривать не один тсоретич. закон распределения F(x)случайной величины X, а тип законов, т. е. семейство законов распределения вида зависящих по крайней мере от двух параметров аи ст. Если ЕX = 0, DX=1, то EY= a, DY=s². Поэтому параметры теоретич. закона имеют следующий смысл а=ЕY и 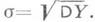Отсюда вытекает способ определения этих параметров по выборке.

Лит.:[1] Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; [2] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., т. 1-2, М., 1964-67; [3] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.

В. Н. Тутубалин.