Akademik

- 1) Н. ф. матрицы A - матрица Nзаранее определенного специального вида, получаемая из Ас помощью преобразований определенного типа. В зависимости от рассматриваемого типа преобразований, от области K, к к-рой принадлежат коэффициенты А , от вида Аи, наконец, от специфики решаемой задачи (напр., от желания расширять или не расширять Kпри переходе от Ак N, от необходимости определить N по А однозначно пли, наоборот, с нек-рым произволом) рассматриваются и различные Н. ф. Часто вместо термина "Н. ф." употребляют термины "каноническая форма", "канонический вид". К числу классических Н. ф. относятся следующие (ниже через обозначается множество всех матриц из тстрок и пстолбцов с коэффициентами из K).

Нормальная форма Смита. Пусть K- либо кольцо целых рациональных чисел, либо кольцо 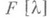многочленов от 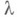с коэффициентами из поля F. Матрица наз. эквивалентной матрице , если найдутся такие обратимые матрицы и , что .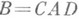. Матрица . Вэквивалентна А тогда и только тогда, когда Вможет быть получена из Ас помощью последовательности элементарных строчных и столбцовых преобразований, т. е. преобразований следующих трех типов: а) перестановка строк (столбцов); б) прибавление к одной строке (столбцу) другой строки (столбца) с множителем из K;в). умножение строки (столбца) на обратимый элемент кольца K. Для преобразований этого типа справедливо следующее утверждение: всякая матрица 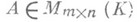эквивалентна матрице вида

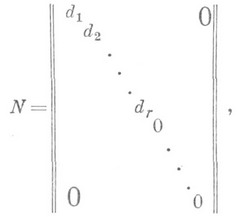
где 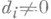при всех делит 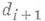при и если , то все 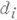положительны, а если , то старшие коэффициенты всех многочленов 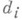равны 1. Указанная матрица Nназ. нормальной формой Смита матрицы А. Элементы наз. инвариантными множителями матрицы А, а число r- ее рангом. Нормальная форма Смита определена по Аоднозначно и может быть найдена следующим образом. Ранг Аравен порядку наименьшего ненулевого минора матрицы А. Пусть ; тогда среди всех миноров порядка 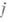матрицы Аимеется хоть один ненулевой. Пусть 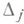, - наибольший общий делитель всех ненулевых миноров порядка jматрицы А(нормированный условием, что при и что старший коэффициент многочлена _j равен 1 при 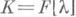) и пусть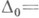 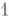. Тогда 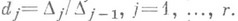Инвариантные множители являются полным набором инвариантов классов эквивалентных матриц: две матрицы из эквивалентны тогда и только тогда, когда у них совпадают ранги и инвариантные множители с равными номерами.

Инвариантные множители раскладываются (единственным способом с точностью до порядка сомножителей) в произведение степеней неприводимых в кольце К элементов (являющихся нек-рыми целыми положительными числами, большими 1, если , и нек-рыми многочленами положительной степени со старшим коэффициентом 1, если ),

где 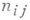- целые неотрицательные числа. Каждый множитель 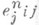, для к-рого , наз. элементарным делителем матрицы А(над К). Каждый элементарный делитель входит в совокупность всех элементарных делителей матрицы Астолько раз, в разложении скольких инвариантных множителей он встречается. Элементарные делители, в отличие от инвариантных множителей, зависят от того, над каким кольцом Крассматривается А: если 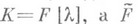- нек-рое расширение поля то матрица

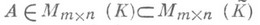имеет, вообще говоря, различные элементарные делители (но одинаковые инвариантные множители) в зависимости от того, рассматривается ли A как элемент или как элемент . Инвариантные множители восстанавливаются по полному набору элементарных делителей и наоборот.

Практический способ нахождения нормальной формы Смита см., напр., в [1].

Указанный основной результат о нормальной форме Смита получен для (см. [71), для 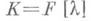(см.[8]). Практически без изменений теория нормальных форм Смита переносится на случай, когда К- любое кольцо главных идеалов (см. [3], [6]). Нормальная форма Смита имеет важные приложения, напр, на ней по существу основывается структурная теория конечно порожденных модулей над кольцами главных идеалов (см. [3], [6]) и, в частности, теория конечно порожденных абелевых групп и теория жордановой Н. ф. (см. ниже).

Естественная нормальная форма. Пусть К- поле. Две квадратные матрицы и наз. подобными над К, если найдется такая невырожденная матрица Имеется тесная связь между подобием и эквивалентностью: матрицы .подобны тогда и только тогда, когда матрицы , где Е- единичная матрица, эквивалентны. Таким образом, для подобия Аи Внеобходимо и достаточно совпадения инвариантных множителей или, что то же,- наборов элементарных делителей над у матриц Практический способ нахождения матрицы Сдля подобных матриц Аи Всм. в [1], [4].

Матрица наз. характеристической матрицей матрицы а инвариантные множители 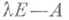наз. инвариантами подобия матрицы А; их пштук. Пусть - инварианты подобия матрицы А. Многочлен равен определителю матрицы и наз. характеристическим многочленом матрицы А. Пусть а степень при больше 1.

Тогда справедливо утверждение: матрица Аподобна над Кблочнодиагональной матрице 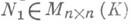вида

где через 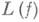для многочлена

обозначена т. н. сопровождающая матрица многочлена

Матрица определена по Аоднозначно и наз. первой естественной Н. ф. матрицы А(см. [1], [2]).

Пусть теперь - набор всех элементарных делителей матрицы . Тогда справедливо следующее основное утверждение: матрица Аподобна над Кблочнодиагональной матрице N₂, блоки к-рой - это сопровождающие матрицы всевозможных элементарных делителей матрицы :

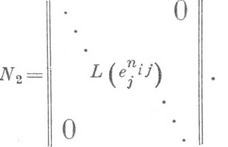
Матрица 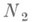определена по Алишь с точностью до порядка следования клеток по главной диагонали; она наз. второй естественной Н. ф. матрицы А(см. [1], [2]), а также еефробениусовой, рациональной, канонической и квазиестественной Н. ф. (см. [4]). В отличие от первой естественной Н. ф., вторая естественная Н. ф., вообще говоря, меняется при переходе от поля Кк его расширению.

Жорданова нормальная форма. Пусть К - поле, - набор всех элементарных делителей матрицы 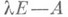над 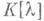. Пусть Кобладает тем свойством, что характеристич. многочлен d_n матрицы Араскладывается в на линейные множители (так будет, напр., если К- поле комплексных чисел или, более общо, любое алгебраически замкнутое поле). Тогда каждый из многочленов имеет вид для нек-рого 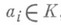, а элементарный делитель соответственно имеет вид 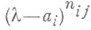. Матрица 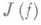иа вида где наз. г пперсопровождающей матрицей многочлена f (см. [1]), или жордановой клеткой порядка s с собственным числом а. Справедливо следующее фундаментальное утверждение: матрица Аподобна над Кблочнодиагональной матрице блоки к-рой - это гиперсопровождающие матрицы всевозможных элементарных делителей матрицы

Матрица J определена лишь с точностью до порядка следования клеток на главной диагонали; она является жордановой матрицей и наз. жордановой Н. ф. матрицы А. Если Кне обладает указанным выше свойством, то Анельзя привести над Кк жордановой Н. ф. (но можно над нек-рым конечным расширением К). О так наз. обобщенной жордановой Н. ф., приведение к к-рой возможно уже над любым полем К, см. [4]. Помимо различных теорий Н. ф. для произвольных матриц возможны соответствующие теории и для матриц какого-либо специального вида. Классическими примерами являются теории Н. ф. симметрия, и косо-симметрич. матриц. А именно, пусть К- поле. Две матрицы наз. конгруэнтными (см. [1]), если найдется такая невырожденная матрица 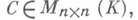что 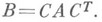Н. ф. относительно отношения конгруэнтности наиболее исследованы для классов симметрич. и кососимметрич. матриц. Пусть и А- кососимметрич. матрица, т. е. . Тогда Аконгруэнтна однозначно определенной матрице H вида

к-рая может рассматриваться как Н. ф. Аотносительно отношения конгруэнтности. Если же А- симметрич. матрица, т. е. 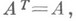то она конгруэнтна матрице Dвида

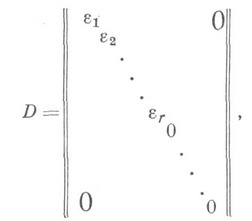
где при всех i. Число r равно рангу Аи определено однозначно, а дальнейшее уточнение выбора элементов e_i зависит от свойств поля К. Так, если Калгебраически замкнуто, то можно считать, что 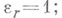если К- поле действительных чисел, то можно считать, что для нек-рого р. Этими свойствами Dуже определена однозначно и может рассматриваться как Н. ф. Аотносительно отношения конгруэнтности. О Н. ф. симметрич. матриц для ряда других полей, а также об эрмитовых аналогах этой теории см. [6], [10] и ст. Квадратичная ферма.

Объединяющим обстоятельством в рассмотренных (а также и других) теориях Н. ф. является то, что допустимые преобразования над рассматриваемым множеством матриц определяются действием нек-рой группы, так что классы матриц, переводимых друг в друга с помощью этих преобразований,- орбиты этой группы, а указание Н. ф. есть выделение в каждой орбите нек-рого канонич. представителя. Так, классы эквивалентных матриц - орбиты группы (где - группы обратимых квадратных матриц порядка sс коэффициентами из К), действующей на по правилу где . 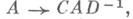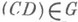Классы подобных матриц - это орбиты группы на 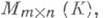действующей по правилу:

Классы конгруэнтных симметрич. или кососимметрич. матриц - это орбиты группы GL_n(K)на множестве всех симметрич. или кососимметрич. матриц порядка п, действующей по правилу где С этой точки зрения каждая теория Н. ф. является конкретным примером решения части общей задачи орбитального разложения для действия нек-рой группы преобразований.

Лит.:[1] Маркус М., Минк X., Обзор по теории матриц и матричных неравенств, пер. с англ., М., 1972; [2] Ланкастер П., Теория матриц, пер. с англ., М., 1978; [3] Ленг С, Алгебра, пер. с англ., М., 1968; [4] Мальцев А. И., Основы линейной алгебры, 4 изд., М., 1975: [5] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [6] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [7] Smith H. J., The Collected Mathematical Paper, v. 1, Oxf., 1894, p. 367-409; [8] Frоbenius G., "J. reine und angew. Math.", 1879, Bd 86, S. 146-208; [9] Гантмахер Ф. Р., Теория матриц, 2 изд., М., 1966; [10] Серр Ж.-П., Курс арифметики, пер. с франц., М., 1972.

В. Л. Попов.

2) Н. ф. оператора - представление с точностью до изоморфизма самосопряженного оператора А, действующего в гильбертовом пространстве , в виде ортогональной суммы операторов умножения на независимую переменную.

Пусть, сначала, А- циклический оператор; это означает, что существует элемент такой, что любой элемент однозначйо представим в виде 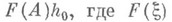- нек-рая функция такая, что

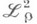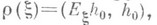здесь - спектральная функция оператора А. Пусть - пространство функций, суммируемых с квадратом на с весом и 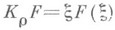- оператор умножения на независимую переменную с областью определения

Тогда операторы Аи Кизоморфны,, т. е. существует изоморфное и изометрич. отображение 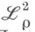такое, что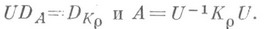

Пусть, теперь, А - произвольный самосопряженный оператор. Тогда Нможно разложить в ортогональную сумму инвариантных подпространств 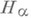, на каждом из к-рых Аиндуцирует циклич. операторы , так что Если на задать оператор то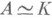

Оператор Кназ. нормальной формой, пли каноническим представлением, оператора А. Теорема о канонич. представлении распространяется на случай произвольных нормальных операторов.

Лит.:[l] Плеснер А. И., Спектральная теория линейных операторов, М., 1965; [2] Ахиезер Н. И., Глазпан И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966.

В. И. Соболев.

3) Н. ф. оператора - представление оператора А, действующего в Фока пространстве, построенном над нек-рым пространством 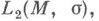где - пространство с мерой, в виде суммы

где - операторнозначные обобщенные функции, порождающие семейства операторов уничтожения и рождения

В выражении (1) в каждом слагаемом множители a(y_j), j = 1, ..., т, стоят правее всех множителей а*( х _i), i=1,..., п, функции (возможно обобщенные) К _{п , т}( х ₁ , ..., х _п ; y₁, ..., у _т )от двух наборов переменных ( х ₁ , ...,х _п)М ⁿ, ( у ₁ ,..., у _т )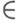М ^т, n, m=0, 1,2, ..., в случае симметричного (бозонного) пространства Фока симметричны по переменным каждого из наборов в отдельности, а в случае антисимметричного (фермионного) пространства Фока - антисимметричны по этим переменным.

Для любого ограниченного оператора Анормальная форма существует и единственна.

Представление (1) можно переписать в виде, непосредственно содержащем операторы уничтожения и рождения:

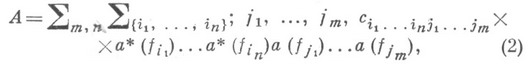
где - нек-рый ортонормированный базис в , и суммирование в (2) происходит

по всем парам конечных наборов 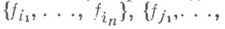элементов этого базиса.

В случае произвольного (сепарабельного) гильбертова пространства НН. ф. оператора А, действующего в пространстве Фока Г (H), построенном над H, определяется при фиксированном базисе в Нс помощью выражения (2), где - семейства операторов уничтожения и рождения, действующих в Г (H).

Лит.:[1] Березин Ф. А., Метод вторичного квантования, М., 1965.

Р. А. Миплос.

4) Н. ф. рекурсивной функции - способ задания n-местной рекурсивной функции j в виде

где f есть (n+1)-местная примитивно рекурсивная функция, g- одноместная примитивно рекурсивная функция,- результат применения наименьшего числа оператора к функции f. Теорема Клини о Н. ф. утверждает: существует такая примитивно рекурсивная функция g, что каждая рекурсивная функция представима в виде (*) с подходящей функцией f, зависящей от , т. е.

Теорема о Н. ф. является одной из важнейших теорем в теории рекурсивных функций.

А. А. Марков [2] получил характеристику тех функций g, к-рые могут использоваться в теореме о Н. ф. в представлении (*). Функция gтогда и только тогда может использоваться в качестве функции, существование к-рой утверждается в теореме о Н. ф., когда уравнение g(x)= ппри любом пимеет бесконечно много решений. Такие функции наз. функциями большого размаха.

Лит.:[l] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; [2] Марков А. А., "Изв. АН СССР. Сер. матем.", 1949, т. 13, № 5, с. 417-24.

В. Е. Плиско.

5) Н. ф. системы дифференциальных уравнений

вблизи инвариантного многообразия М- такая формальная система

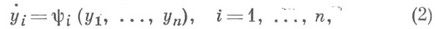
к-рая получается из (1) обратимой формальной заменой координат

и в к-рой ряды Тейлора - Фурье y_i содержат только резонансные члены. Впервые Н. ф. для одного случая встречается в диссертации А. Пуанкаре (Н. Poincare, см. [1]). Посредством Н. ф. (2) нек-рые системы (1) интегрируются, многие исследуются на устойчивость и интегрируются приближенно, для систем (1) отыскиваются периодич. решения и семейства условно перио-дич. решений, изучаются их бифуркации.

Н. ф. в окрестности неподвижной точки. Пусть М- неподвижная точка системы (1) (т. е. ), функции аналитичны в ней и - собственные значения матрицы 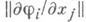при X= 0. Пусть Тогда в полной окрестности точки X =0 система (1) имеет следующую Н. ф. (2): матрица 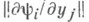при 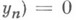имеет Н. ф. (напр., жорданову), а ряды Тейлора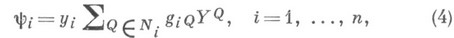

содержат только резонансные члены, для к-рых

Если уравнение (5) не имеет в решений то Н. ф. (2) является линейной:

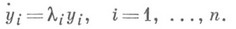
Всякая система (1) с в окрестности неподвижной точки приводится к своей Н. ф. (2) нек-рым формальным преобразованием (3), где - степенные ряды (возможно, расходящиеся), и при Y = 0.

Вообще говоря, нормализующее преобразование (3)и Н. ф. (2) (т. е. коэффициенты в (4)) неоднозначно определяются исходной системой (1). Н. ф. (2) сохраняет мпогие свойства системы (1): вещественность, симметричность, гамильтоновость и др. (см. [2], [3]). Если в исходной системе имеются малые параметры, то их можно включить в число координат , тогда 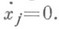При нормализующем преобразовании такие координаты не меняются (см. [3]).

Если k- число линейно независимых решений уравнения (5), то с помощью преобразования

где 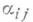- целые иН. ф. (2) переводится

в систему вида

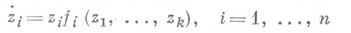
(см. [2], [3]). Решение этой системы сводится к решению подсистемы из первых куравнений и к п-к квадратурам. Подсистему надо исследовать в окрестности сложной особой точки 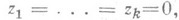ибо не содержат линейных членов. Это можно сделать с помощью локального метода (см. [3]).

Рассматривался вопрос (см. [2]): при каких условиях на Н. ф. (2) сходится (аналнтично) нормализующее преобразование аналитической системы (1)? Пусть

по таким для к-рых

в. Условие:

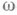
Условие :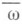

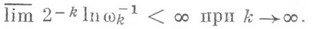
Условие слабее условия w. Оба они выполнены для почти всех 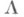(по мере Лебега) и являются очень слабыми арифметич. ограничениями на .

Условие А в случае (общий случай см. в [2] ): существует такой степенной ряд , что в (4)

Если аналитич. системы (1) Л удовлетворяет условию w и Н. ф. (2) удовлетворяет условию А, то существует аналитич. реобразование системы (1) к нек-рой Н. ф. Если Н. ф. (2) получается из нек-рой аналитич. системы и не удовлетворяет хотя бы одному из условий 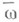и А, то существует такая аналитич. система (1), к-рая имеет (2) своей Н. ф. и всякое преобразование к-рой к Н. ф. расходится (не аналитично).

Таким образом, поставленный выше вопрос решен для всех Н. ф., кроме тех, у к-рых 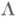удовлетворяет условию и не удовлетворяет условию , а остальные коэффициенты Н. ф. удовлетворяют условию А. Условие А является очень жестким ограничением на коэффициенты Н. ф., и для больших поно выполнено, вообще говоря, только в вырожденных случаях. Т. е. основная причина расходимости преобразований к Н. ф.- это не малые знаменатели, а невырожденность Н. ф.

Но и в случаях расходимости нормализующего преобразования (3) по Н. ф. (2) можно изучить свойства решений системы (1). Так, для вещественной системы (1) гладкое преобразование к Н. ф. (2) существует и в тех случаях, когда нет аналитического. Большинство результатов о гладкой нормализации получено при условии, что все При этом условии с помощью замены конечного класса гладкости систему (1) можно привести к укороченной Н. ф.

где - многочлены степени т(см. [4] - [6]). Если в нормализующем преобразовании (3) отбросить все члены степени выше т, то получится преобразование

(- многочлены), к-рое приводит (1) к виду

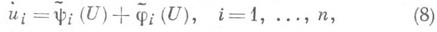
где - многочлены, содержащие только резонансные члены,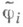- сходящиеся степенные ряды, содержащие только члены степени выше т. Решения укороченной Н. ф. (6) служат приближениями для решений системы (8) и после преобразования (7) дают приближения решений исходной системы (1). Во многих случаях для (6) удается построить такую Ляпунова функцию (или Четаева функцию) f(V), что

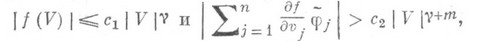
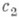где и - положительные постоянные. Тогда f(U)будет функцией Ляпунова (Четаева для системы (8), т. е. точка X= 0 будет устойчивой (неустойчивой). Напр., если все 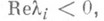то можно взять т -1, и получится теорема Ляпунова об устойчивости по линейному приближению (см. [7]; другие примеры см. в обзоре [8]).

По Н. ф. (2) можно находить инвариантные аналитические множества системы (1). В дальнейшем для простоты изложения предполагается, что Rе L= 0. По Н. ф. (2) выделяется формальное множество

где а- свободный параметр. На множестве выполняется условие А. Пусть К- объединение таких подпространств вида что соответствующие собственные значения 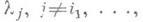попарно соизмеримы. Формальное множество аналитично в системе (1). Из выделяется подмножество , к-рое аналитично в системе (1), если выполнено условие (см. [3]). На множествах и лежат периодич. решения и семейства условно перподич. решений системы (1). Рассматривая множества и в системах с малыми параметрами, можно изучить все аналитич. возмущения и бифуркации таких решений (см. [9]).

Обобщения. Если систему (1) приводить не к Н. ф. (2), а к системе, правые части к-рой содержат нек-рые нерезонансные члены, то упрощение получается менее значительным, зато можно улучшить качество преобразования. Так, приведение к "полунормальной форме" будет аналитическим при ослабленном условии А (см. [2]). Другой вариант - преобразование, нормализующее систему (1) лишь на нек-рых подмногообразиях (напр., на нек-рых координатных подпространствах; см. [2]). Комбинации этих подходов позволяют доказать для системы (1) существование инвариантных подмногообразий и решений определенного вида (см. [9]).

Пусть система (1) определена и аналитична в окрестности инвариантного многообразия Мразмерности k+l, к-рое расслаивается на l-мерные инвариантные торы. Тогда вблизи Мможно ввести такие локальные координаты

что на 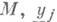имеют период 2 , Sпробегает нек-рую область Н, и система (1) принимает вид

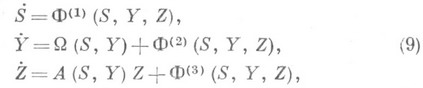
где 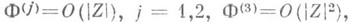А-матрица.

Если = const и матрица Атреугольна с постоянной главной диагональю , то (при слабом ограничении на малые знаменатели) существует формальное преобразование локальных координат S, Y, к-рое приводит систему (9) к Н. ф.

Если среди координат Z есть малый параметр, то систему (9) можно осреднить Крылова- Боголюбова методом усреднения (см. [10]), и осредненная система будет Н. ф. Вообще, теорию возмущений можно рассматривать как частный случай теории Н. ф., когда одна из координат является малым параметром (см. [11]).

На системы (9) и (10) переносятся теоремы о сходимости нормализующей замены, теоремы о существовании аналитических инвариантных множеств и т. д. Здесь наиболее изучен случай, когда М- периодич. решение, т. е. к= 0, l =1. В этом случае теория Н. ф. во многом идентична случаю, когда М- неподвижная точка. А. Пуанкаре предложил рассматривать точечное преобразование нормального сечения за период. В связи с этим возникла теория Н. ф. точечных отображений, к-рая параллельна соответствующей теории для систем (1). Другие обобщения Н. ф. см. в [3], [б], [12], [1З].

Лит.:[1] Пуанкаре А., Избр. труды, пер. с франц., т. 3, М., 1974; [2] Брюно А. Д., "Тр. Моск. матем. об-ва", 1971, т. 25, с. 119-262; 1972, т. 26, с. 199 - 239; [3] его же, Локальный метод нелинейного анализа дифференциальных уравнений, М., 1979; [4] Xартман Ф., Обыкновенные дифференциальные уравнения, пер. с англ., М., 1970; [5.1 Самовол В. С, "Докл. АН СССР", 1972, т. 206, № 3, с. 545 - 48; [6] Белицкий Г. Р., Нормальные формы, инварианты и локальные отображения. К., 1979; [7] Ляпунов А. М., Общая задача об устойчивости движения, 2 изд., М.- Л., 1935; [8] Куницын А. Л., Маркеев А. П., Итоги науки и техники. Сер. Общая механика, т. 4, М., 1979, с. 58-139; [9] Bibi'kov J. N.. Local theory of nonlinear analytic ordinary differential equations, В. [а. о.], 1979; [10] Боголюбов H. H., Митропольский Ю. А., Асимптотические методы в теории нелинейных колебаний, 4 изд., М., 1974; [11] Брюно А. Д., "Рrос. VIII Intern. Conf. on Nonlinear Oscillations", Prague, 1979, v. 1, p. 177-82; [12] Костiн В. В., Ле Дiнь Тхюi, "Доповiдi АН УРСР. Сер. А", 1975, № 11, с. 982-85; [13] Zehnder E. J., "Manus. math.", 1978, v. 23, p. 363-71.

А. Д. Брюно.