Akademik

- распределение вероятностей случайной величины Х _п, принимающей целые неотрицательные значения k,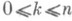, в соответствии с 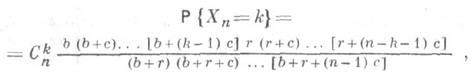формулой

где целые 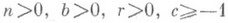- параметры, или эквивалентной формулой

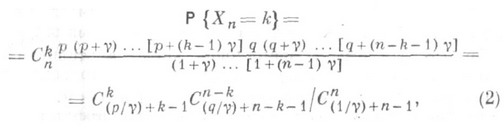
где целое n>0, действительные 0<р<1, q=1-р,g>0 - параметры. Связь между (1) и (2) устанавливается равенствами

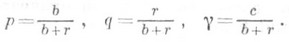
Математич. ожидание и дисперсия П. р. равны соответственно 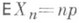и 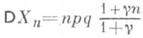. Специальные

случаи П. р.: ХД имеет при c=0 биномиальное распределение с параметрами n и р; Х _n имеет при s=-1 гипергеометрическое распределение с параметрами М=b, N=b+r и п. При 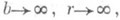когда p=b/(b+r).постоянно, и 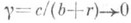, П. р. стремится к биномиальному распределению с параметрами пи р.

П. р. было рассмотрено Д. Пойа (G. Polya, 1923) в связи с т. н. урновой схемой Пойа. Из урны, содержащей bчерных и rкрасных шаров, осуществляется выбор с возвращением при условии, что каждый извлеченный шар возвращается в урну вместе с сшарами того же цвета. Если Х _п - полное число черных шаров в выборке объема п, то распределение Х _n задается формулами (1) или (2). Последовательность Х _n, п=1,2, ..., представляет собой дискретный марковский процесс, причем состояния процесса определяются числом черных шаров в выборке в момент п, а условная вероятность перехода от состояния kв момент времени n в состояние k+1 в момент времени n+1 равна

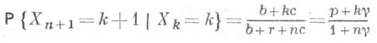
(зависит от п).

Предельным переходом из урновой схемы Пойа может быть получен процесс Пойа - неоднородный марковский процесс с непрерывным временем, принадлежащий классу процессов "чистого размножения". При условии, что за бесконечно малое время Dtпроисходит лишь одно извлечение шара, при , когда 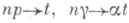, выводится предельная условная вероятность перехода из состояния kв состояние k+1 за время Dt:

При переходе от урновой схемы Пойа к процессу Пойа возникает важная предельная форма П. р. Именно, вероятность Р _k(t).в момент времени tпребывать в состоянии kравна

Полученное предельное распределение является отрицательным биномиальным распределением с параметрами 1/a и 1/(1+at) (соответствующее математич. ожидание равно t, а дисперсия t(1+at).

Урновая модель и процесс Пойа, в к-рых возникает П. р. и его предельная форма, являются моделями с эффектом последействия (извлечение шара определенного цвета из урны увеличивает вероятность извлечения шара того же цвета при следующем испытании).

При стремлении параметра a к нулю процесс Пойа переходит в пуассоновский процесс, а П. р. при имеет своим пределом Пуассона распределение с параметром t.

Лит.:[1] Феллер В., Введение в теорию вероятностей и ее приложения, пер. е англ., 2 изд., т. 1-2, М., 1967.

А. В. Прохоров.