Akademik

КОГЕРЕНТНОСТЬ

КОГЕРЕНТНОСТЬ: (от лат. cohaerens— находящийся в связи), согласованное протекание во времени и в пр-ве неск. колебат. или волн. процессов, проявляющееся при их сложении. Колебания наз. когерентными, если разность их фаз остаётся постоянной (или закономерно изменяется) во времени и при сложении колебаний определяет амплитуду суммарного колебания. Гармонич. колебание описывается выражением:

Р(t)=Acos(wt+j), (1)

где Р — изменяющаяся величина (смещение маятника, напряжённость электрич. и магн. полей и т. д.), а амплитуда А , частота со и фаза j — константы. При сложении двух гармонич. колебаний с одинаковой частотой со, но разными амплитудами A1 и А2 и фазами j1 и j2 образуется гармонич. колебание той же частоты. Амплитуда результирующего колебания

Ар =?(A21+A22+2A1A2cos(j1-j2)) (2)

может изменяться в пределах от A1+A2 до AI-A2 в зависимости от разности фаз j1-j2 (рис.).

В действительности идеально гармонич. колебания неосуществимы. В реальных колебат. процессах амплитуда, частота и фаза колебаний могут непрерывно хаотически изменяться во времени.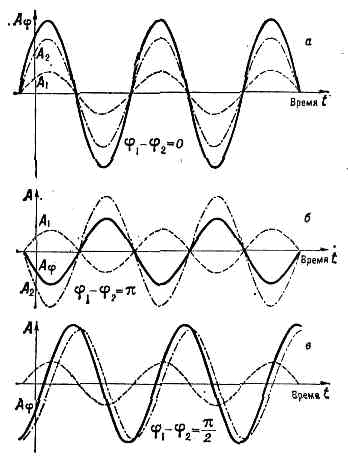

Сложение двух гармонич. колебаний (пунктир) с амплитудами A1 и A2 при разл. разностях фаз. Результирующее колебание — сплошная линия.

Если фазы двух колебаний j1 и j2 изменяются беспорядочно, но их разность j1-j2 остаётся постоянной, то амплитуда суммарного колебания определяется разностью фаз складываемых колебаний, т. е. колебания когерентны. Если разность фаз двух колебаний изменяется очень медленно, то в этом случае колебания остаются когерентными лишь в течение нек-рого времени, пока их разность фаз не успела измениться на величину, сравнимую с я.

Если сравнивать фазы одного и того же колебания в разные моменты времени, разделённые интервалом т, то при достаточно большом т случайное изменение фазы колебания может превысить л. Это означает, что через время т гармонич. колебание «забывает» свою первонач. фазу и становится некогерентным «самому себе». С ростом т К. обычно ослабевает постепенно. Для количеств, хар-ки этого явления вводят ф-цию R (t), наз. функцией корреляции. Результат сложения двух колебаний, полученных от одного источника и задержанных друг относительно друга на время t, можно представить с помощью R (t) в виде:

Ар = ?(A21+A22+2A1A2R (t)coswt) , (3)

где w — ср. частота колебания. Ф-ция R(t)=1 при t=0 и обычно спадает до 0 при неогранич. росте t. Значение т, при к-ром R(t)=0,5, наз. временем когерентности или продолжительностью гармонич. цуга. По истечении одного гармонич. цуга колебаний он как бы заменяется другим с той же частотой, но с другой фазой.

Хар-р и св-ва колебат. процесса существенно зависят от условий его возникновения. Напр., свет, излучаемый газовым разрядом в виде узкой спектр. линии, может быть близок к монохроматическому. Излучение такого источника складывается из волн, посылаемых разл. ч-цами независимо друг от друга и поэтому с независимыми фазами (спонтанное излучение). В результате амплитуда и фаза суммарной волны хаотически изменяются с характерным временем, равным времени К. Изменения амплитуды суммарной волны велики: от 0, когда исходные волны гасят друг друга, до макс. значения, когда соотношение фаз исходных волн благоприятствует их сложению. Колебания, возникающие в автоколебат. системе, напр. в ламповом или транзисторном генераторах, лазере, имеют др. структуру. В первых двух частота и фаза колебаний хаотически изменяются, но результирующая амплитуда поддерживается постоянной. В лазере все ч-цы излучают согласованно (вынужденное излучение), синфазно с колебанием, установившимся в резонаторе. Соотношения фаз слагающих колебаний всегда благоприятны для образования устойчивой амплитуды суммарного колебания. Термин «К.» иногда означает, что колебание порождено автоколебат. системой и имеет стабильную амплитуду.

При распространении плоской эл.-магн. волны в однородной среде фаза колебаний в к.-н. определ. точке пр-ва сохраняется только в течение времени К. t0. За это время волна распространяется на расстояние ct0. При этом колебания в точках, удалённых друг от друга на расстояние, большее ct0, вдоль направления распространения волны, оказываются некогерентными. Расстояние, равное ct0 вдоль направления распространения плоской волны, наз. длиной К. или длиной цуга.

Идеально плоская волна неосуществима, как и идеально гармонич. колебание. В реальных волн. процессах амплитуда и фаза колебаний изменяются не только вдоль направления распространения волны, но и в плоскости, перпендикулярной этому направлению. Случайные изменения разности фаз в двух точках, расположенных в этой плоскости, увеличиваются с расстоянием между ними. К. колебаний в этих точках ослабевает и на нек-ром расстоянии l, когда случайные изменения разности фаз становятся сравнимыми с я, исчезает. Для описания когерентных св-в волны в плоскости, перпендикулярной направлению её распространения, применяют термины площадь К. и пространственная К., в отличие от временной К., связанной со степенью монохроматичности волны. Количественно пространств. К. также можно характеризовать ф-цией корреляции RI(l). Условие Rf(l)=0,5 определяет размер или радиус К., к-рый может зависеть от ориентации отрезка l в плоскости, перпендикулярной направлению распространения волны. Всё пр-во, занятое волной, можно разбить на области, в каждой из к-рых волна сохраняет К. Объём такой области (объём К.) принимают равным произведению длины цуга на площадь фигуры, ограниченной кривой RI(l)=0,5RI(0).

Нарушение пространств. К. связано с особенностями процессов излучения и формирования волн. Напр., нагретое тело излучает совокупность сферич. волн, распространяющихся по всем направлениям. По мере удаления от теплового источника конечных размеров волна приближается к плоской. На больших расстояниях от источника размер К. равен l,22lr/r, где r — расстояние до источника, r — размер источника. Для солн. света размер К. равен 30 мкм. С уменьшением утл. размера источника размер К. растёт. Это позволяет определить размер звёзд по размеру площади К. приходящего от них света. Величину l/r наз. углом К. С удалением от источника интенсивность света убывает пропорц. 1/r2. Поэтому с помощью нагретого тела нельзя получить интенсивное излучение, обладающее большой пространств. К. Световая волна, излучаемая лазером, формируется в результате вынужденного излучения во всём объёме активного в-ва. Поэтому пространств. К. лазерного излучения сохраняется во всём поперечном сечении луча.

Понятие «К.», возникшее первоначально в классич. оптике как хар-ка, определяющая способность света к интерференции (см. ИНТЕРФЕРЕНЦИЯ СВЕТА), широко применяется при описании колебаний и волн любой природы. Благодаря квант. механике, распространившей волн. представления на все процессы в микромире, понятие «К.» стало применяться к пучкам эл-нов, протонов, нейтронов и др. ч-ц. Здесь под К. понимают упорядоченные согласованные и направленные движения большого кол-ва квазинезависимых ч-ц. Понятие «К.» проникло также в теорию тв. тел (напр., гиперзвуковые фононы, (см. ГИПЕРЗВУК)) и квант. жидкостей. После открытия сверхтекучести жидкого гелия появилось понятие «К.», означающее, что макроскопич. кол-во атомов жидкого сверхтекучего гелия может быть описано единой волн. ф-цией, имеющей одно собств. значение, как будто это одна ч-ца, а не ансамбль огромного числа взаимодействующих ч-ц.

КОГЕРЕНТНОСТЬ

(от лат. cohaerens -находящийся в связи) - коррелированное протекание во времени и в пространстве неск. случайных колебат. или волновых процессов, позволяющее получить при их сложении чёткую интерференц. картину. Первоначально понятие К. возникло в оптике, однако оно относится к волновым полям любой природы: эл.-магн. волнам произвольного диапазона, упругим волнам, волнам в плазме, квантовомеханич. волнам амплитуды вероятностей и т. д.

Существование интерференц. картины является прямым следствием суперпозиции принципа для линейных колебаний и волн. Однако в реальных условиях всегда существуют хаотич. флуктуации волнового поля, в частности разности фаз взаимодействующих волн, что приводит к быстрому перемещению интерференц. картины в пространстве. Если через каждую точку за время измерения успевают многократно пройти максимумы и минимумы интерференц. картины, то зарегистрированное ср. значение интенсивности волны окажется в разл. точках одинаковым и интерференц. полосы расплывутся. Чтобы зарегистрировать чёткую интерференц. картину, необходима такая стабильность случайных фазовых соотношений, при к-рой смещение интерференц. полос за время измерения составляет лишь небольшую часть от их ширины. Поэтому качеств. понятие К. можно определить как необходимую стабильность случайных фазовых соотношений за время регистрации интерференц. картины.

Такое качеств. понятие К. в ряде случаев оказывается неудобным или недостаточным. Напр., при разл. способах регистрации интерференц. картины может оказаться, что необходимое для этого время различно, так что волна, когерентная по результатам одного эксперимента, некогерентна по результатам другого. В связи с этим удобно иметь количеств. меру степени когерентности, не зависящую от способа измерения интерференц. картины.

Если волновое поле 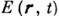описывается при помощи комплексной амплитуды 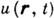, так что 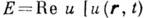может быть, напр., аналитическим сигналом], то функция взаимной когерентности второго порядка Г ₂ определяется как ср. значение:

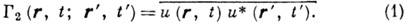
Черта сверху обозначает статистич. усреднение по флуктуациям волнового поля, причём флуктуировать могут как фаза, так и амплитуда волны; * означает комплексное сопряжение. Случайная (мгновенная) интенсивность (плотность энергии) волны пропорц. величине 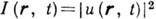. Её ср. значение связано с Г ₂ ф-лой 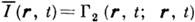. Ср. вектор плотности потока энергии S также выражается через Г":

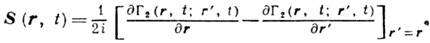
Для многокомпонентного (напр., эл.- магн.) поля скалярная ф-ция Г ₂ заменяется тензором второго ранга. Если суммарное волновое поле 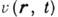в нек-рой точке является результатом сложения исходных полей

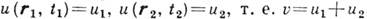, то его ср. интенсивность 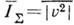выражается через и ₁ и и ₂ ф-лой

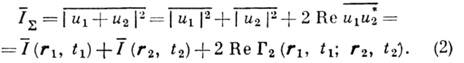
Величину

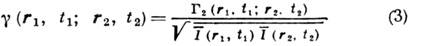
наз. комплексной степенью когерентно с-т и полей в пространственно-временных точках

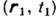и 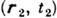. Из (3) следует, что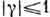

Чёткость интерференц. картины непосредственно связана с величиной 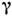. Если интенсивности интерферирующих пучков одинаковы (чего всегда можно добиться в эксперименте), т. е. 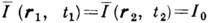, то на основании (2) можно записать

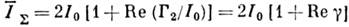
Если представить 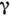в виде 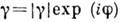, то 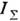= =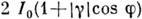. Обычно в пределах интерференц. картины 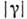изменяется гораздо слабее, чем соs j. В этом случае максимумы распределения 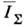соответствуют тем местам, где 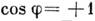, а минимумы - значениям 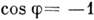, тогда 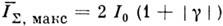, , 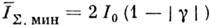а для относит. контраста пн-терференц. картины (её "видности")

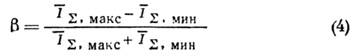
получаем

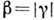
Т. о., "видность" интерференц. картины непосредственно выражается через степень когерентности, т. е. в конечном счёте через ф-цию Г ₂. Максимально чёткой интерференц. картине, в к-рой 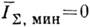, соответствует значение 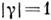. Полностью замытой интерференц. картине, в к-рой 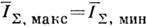, соответствует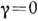

Величину 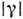можно непосредственно измерить при помощи соотношения (4), если предварительно обеспечить равенство ср. интенсивностей 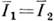. Величина 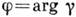определяет смещение интерференц. полос.

Из определения 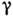следует, что степень когерентности максимальна при совмещении точек наблюдения: 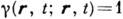. Характерный масштаб 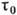спадания ф-ции 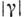попеременной 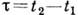наз. временем когерентности. Если при наложении волновых полей временной сдвиг 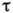между ними мал по сравнению с 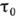, то может быть подучена чёткая интерференц. картина. В противоположном случае интерференция наблюдаться не будет. Величина 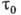также ограничивает время измерения интерференц. картины, о к-ром говорилось выше. Величина 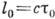, где с - скорость распространения волны рассматриваемого типа, наз. продольным радиусом когерентности (длиной когерентности).

Если рассмотреть волновой пучок с чётко выделенным направлением распространения, то при разнесении точек наблюдения поперёк этого направления ф-ция 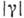также будет убывать. Характерный масштаб спада-ния 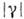в этом случае наз. поперечным радиусом когерентности r₀. Эта величина характеризует размер тех участков волнового фронта, от к-рых может быть получена чёткая интерференц. картина. По мере распространения волны в однородной среде величина r₀ возрастает за счёт дифракции (см. Ван-Циттерта-Цернике теорема). Произведение 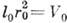характеризует объём когерентности, в пределах к-рого случайная фаза волны меняется на величину, не превосходящую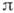

К. волновых полей можно исследовать и косвенным путём, изучая корреляцию флуктуации мгновенной интенсивности I. При этом время измерения должно быть малым по сравнению с 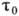, а поперечный размер детектора - малым по сравнению с r₀. Корреляц. ф-цию флуктуации интенсивности -

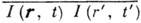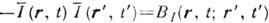можно найти, если наряду с Г ₂ известна и ф-ция К. четвёртого порядка:

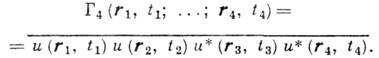
Если случайное поле u(r, t )является гауссовым (напр., создаётся тепловым источником), причём 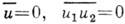(но, разумеется, 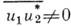), то Г ₄ можно выразить через Г ₂ по ф-лам, справедливым для гауссовых случайных полей:

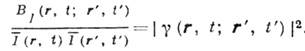
Поэтому для гауссовых волновых полей измерения величины B_I могут дать сведения о модуле степени К. 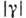(см. Интерферометр интенсивности). В общем случае измерений интенсивности волнового поля в п точках для описания результатов опыта достаточно знать ф-цию К. порядка 2п:

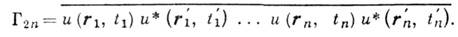
Эти же ф-ции описывают результаты экспериментов по статистике фотоотсчётов, когда измеряются корреляции чисел фотонов, зарегистрированных в разл. точках r₁, . .., r_п.

Квантовые шумы могут существенно исказить результаты интерференц. опыта, если полное число фотонов, зарегистрированных в максимуме интерференц. картины, невелико. Т. к. при осуществлении интерференц. опыта можно собрать излучение с площади, имеющей порядок величины 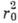, и проводить измерения в течение времени 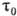, то при этом будут использованы все фотоны из объёма 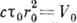, т. е. из объёма коге-рентпости. Если ср. число N фотонов в объёме К., называемое параметром вырождения, велико, то квантовые флуктуации числа зарегистрированных фотонов относительно невелики (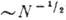) и не оказывают существ, влияния на результат измерений. Если же N невелико, то эти флуктуации будут препятствовать измерениям.

Термин "К." употребляется и в более широком смысле. Так, в квантовой механике состояния, для к-рых реализуется минимум в неопределённостей соотношении, наз. когерентными состояниями. В разл. областях физики термин "К." применяется для описания корре-лиров. поведения большого числа частиц (как это имеет место, напр., при сверхтекучести). Термин "когерентные структуры" в разл. областях науки применяется для обозначения спонтанно возникающих устойчивых образований, сохраняющих нек-рые закономерные свойства на фоне хаотич. флуктуации.

Лит.: Вольф Э., Мандель Л., Когерентные свойства оптических полей, пер. с англ., "УФН", 1965, т. 87, с. 491; 1966, т. 88, с. 347, 619; О' Н е и л Э., Введение в статистическую оптику, пер. с англ., М., 1966; Борн М., Вольф Э. Основы оптики, пер. сангл., 2 изд., М., 1973; Клаудер Д ж. Сударшан Э., Основы квантовой оптики, пер. с англ. М., 1970; Перина Я., Когерентность света, пер. с англ. М., 1974. В. И. Татарский

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.