Akademik

ПЛАСТИЧНОСТИ ТЕОРИЯ

ПЛАСТИЧНОСТИ ТЕОРИЯ: раздел механики, в к-ром изучаются законы, отражающие связи между напряжениями и упругопластич. деформациями (физ. основы П. т.), и разрабатываются методы решения задач о равновесии и движении деформируемых тв. тел (матем. П. т.). П. т. явл. основой совр. расчётов конструкций, сооружений и машин с учётом макс. использования прочностных и деформац. ресурсов материалов, а также расчётов технологич. процессов обработки металлов давлением (ковки, штамповки и др.) и ряда природных процессов (горообразования, дрейфа континентов и др.).

Упругие деформации конструкц. материалов имеют величину 0,3—0,5%, тогда как пластич. деформации до разрушения достигают значений 10— 20% и более, а напряжения при разрушении превышают предел текучести в неск. раз. Поэтому методы расчёта, основанные на допустимости только упругих деформаций, не всегда технически и экономически целесообразны. Более того, иногда создание жизнеспособной конструкции просто невозможно без учёта стадии пластич. деформации.

Физические основы П. т. Физ. основой П. т. явл. законы связи между напряжениями и деформациями (см. ПЛАСТИЧНОСТЬ) в разл. термомеханич. условиях. Для пластичности типично, что значения напряжений зависят не только от текущих значений деформаций, но и от предшествующего процесса их изменения. Напр., если тонкостенный трубчатый образец вначале растянуть до относит. удлинения e1, а потом при неизменном e1 закрутить до деформации сдвига g1; то в конце этого процесса норм. и касат. напряжения в поперечном сечении образца достигают нек-рых значений s1t1. Если такой же образец вначале закрутить до той же деформации сдвига g1, а потом при постоянном g1 растянуть до относит. удлинения e1, то в этом процессе норм. и касат. напряжения достигают значений s'1t'1, отличных от s1t1.

В общем случае процесс деформации описывается шестью ф-циями изменения компонентов тензора деформации (см. ДЕФОРМАЦИЯ МЕХАНИЧЕСКАЯ), однако его удобно также представлять графически. Напр., при совместном растяжении и кручении трубчатого образца деформированное состояние изображается в прямоугольной системе координат Oэ1э2 точкой М (рис. 1), координаты к-рой по оси э1=e, а по оси э2=g/?3 (множитель 1/?3 вводится в связи с тем, что предел текучести при растяжении в ?3 раз отличается от предела текучести при сдвиге), или вектором деформации э=ОМ. Модуль вектора э равен интенсивности деформации eu. В процессе деформации точка М (э1, э2) очерчивает кривую OL, к-рая наз. т р а е к т о р и е й д е ф о р м а ц и и. Степень сложности процесса характеризуется кривизной траектории деформации k, к-рая явл. ф-цией длины дуги s траектории: k=k(s).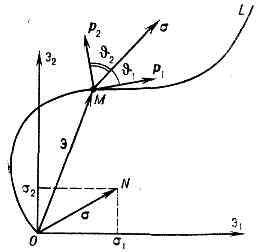

Рис. 1. График, изображающий процесс деформации трубчатого образца.

Эта функция определяет т. н. внутреннюю геометрию траектории. Деформация наз. п р о с т о й, если все компоненты тензора деформации возрастают пропорционально одному параметру (напр., времени или длине дуги s). Траектория простой деформации — прямолинейный луч ОК (рис. 2); её кривизна k(s)=0, причём s=eu. При сложной деформации k(s)?0 (кривая OL). Частный случай сложной деформации — двухзвенный процесс, изображаемый ломаной (напр., OCD).

Напряжённое состояние можно изображать на плоскости (э1, э2) в виде вектора напряжений s=ON® (рис. 1) с координатами s1=s, s2=t?3. Начало этого вектора относят к той точке траектории деформации, в к-рой это напряженное состояние достигнуто. Если в одном образце точка М достигнута путём процесса OL (рис. 2), а в другом, идентичном, путём процесса OL', то векторы напряжений s и s' в этой точке различны.

Зависимость нек-рой величины в момент t от процесса изменения другой величины в интервале (0, t) описывается матем. объектом, к-рый наз. функционалом. При пластич. деформации напряжения — функционалы процесса деформации, а также давления, темп-ры и скорости деформации.

Теория малых у п р у г о п л а с т и ч е с к и х д е ф о р м а ц и й. При простой активной деформации, когда интенсивность деформации eu возрастает, имеют место соотношения теории малых упругопластич. деформаций (А. А. Ильюшин, 1943):

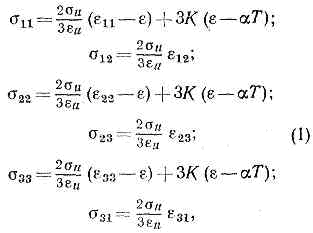к-рые означают, что а) вектор напряжений коллинеарен лучу деформации (sA на рис. 2); б) его модуль— функция eu, давления q, темп-ры Т и скорости изменения интенсивности деформации eu=deu/dt, не зависящая от направления луча деформации; в) относит. изменение объёма q=3e=e11+e22+e33 пропорционально среднему напряжению s=1/3(s11+s22+s33) и темп-ре.

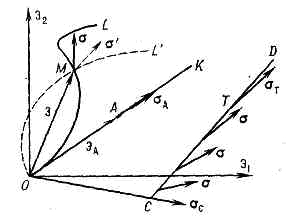Рис. 2. Траектории деформации: ОК — при простой деформации, k(s)=0; OL — при произвольном сложном процессе, k(s)?0; OCD — двухзвенный процесс кручения трубчатого образца при постоянном удлинении; k(s)=0 всюду, кроме точки С, где k(s)=?.

Здесь К — модуль объёмной упругости (см. МОДУЛИ УПРУГОСТИ), a — коэфф. линейного теплового расширения, su=Ф(eu, q, Т, eu) — экспериментально определяемая ф-ция, к-рая при неизменных q, Т и eu наз. ф у н к ц и е й у п р о ч н е н и я. При пассивной деформации (eu убывает), т. е. при разгрузке, приращения напряжений и деформаций связаны соотношениями обобщённого Гука закона. Теория малых упругопластич. деформаций используется в практике расчётов конструкций и сооружений на прочность и устойчивость при пластич. деформациях.

Теория течения С е н-Ве н а н а. Франц. учёный А. Сен-Венан (1871) предположил, что в сложном процессе активной деформации идеально пластич. (неупрочняющегося) материала, для к-рого интенсивность напряжений su постоянна и равна пределу текучести ss при активной пластич. деформации, вектор напряжений коллинеарен касательной к траектории деформации и материал механически несжимаем. При изотермич. условиях соотношения напряжения — деформации по его теории имеют вид

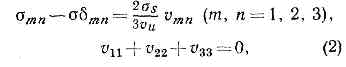где vmn — компоненты тензора скоростей деформации, vu — интенсивность скоростей деформации, dmn — символ Кронекера: dmn=1 при т=п и dmn=0 при m?n. Соотношения (2) хорошо согласуются с данными опытов только при простой деформации и в процессах малой кривизны (см. ниже). Теория течения Сен-Венана успешно используется при расчётах технологич. процессов формоизменения неупрочняющихся или слабоупрочняющихся металлов (штамповки, прессования и др.). При расчётах горячих скоростных процессов необходимо учитывать зависимость ss от темп-ры и скорости деформации.

При сложном процессе деформации к построению соотношений между напряжениями и деформациями имеется несколько подходов.

Теория упругопластических процессов. При совместном растяжении и кручении трубчатого образца вектор напряжений можно представить в виде s=suX(p1cosq1+p2cosq2), где единичные векторы касательной р1 и нормали р2 к траектории деформации образуют т. н. репер Ф р е н е, а q1 и q2 — углы ориентации вектора напряжений, т. е. углы между а и р1 и p2 соответственно (рис. 1), причём q2=p/2-q1. Если величины su и q?q1 определены как функции процесса (функционалы), то написанное выражение для о даёт связь между напряжениями и деформациями.

В общем случае сложного напряжённого состояния процесс изменения девиатора деформации изображается в пятимерном пространстве траекторией деформации, внутр. геометрия к-рой описывается кривизнами k1(s), k2(s), k3(s), k4(s), а репер Френе определяется пятью единичными векторами р1, p2, p3,,p4, p5. Параметрами, определяющими процесс деформации, явл.: ориентация траектории, её внутр. геометрия (кривизны), давление q, темп-pa Т и скорость деформации s=ds/dt, заданные как ф-ции длины дуги s. Вектор напряжений а определяется модулем |s|= su и углами ориентации:

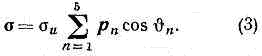Задачей теории явл. установление зависимости величин su, q1, q2, q3, q4, q5 от параметров произвольного процесса деформации.

Осн. законом теории упругопластич. процессов явл. постулат изотропии А. А. Ильюшина, согласно к-рому для изотропного материала модуль вектора напряжении и углы его ориентации в репере Френе однозначно определяются изменением параметров процесса от его начала до текущего момента, т. е. они явл. функционалами, порождаемыми ф-циями k1(s), k2(s), k3(s), k4(s), q(s), T(s), s(s), и не зависят от ориентации траектории деформации. Действительно, в опытах обнаружено, что если в трёх одинаковых образцах из изотропного материала, испытываемых, напр., при совместном растяжении и кручении, осуществить процессы деформации OL, OL', OL" (рис. 3) с одинаковой внутренней геометрией k(s)=k'(s)=k"(s) (траектория OL' построена путём отражения OL в нек-ром луче ОА, а траектория OL" -- поворотом OL на нек-рый угол), то в точках М, М', М" с одинаковыми значениями длины дуги (ОМ=ОМ'=ОМ") модули векторов напряжений и углы их ориентации одинаковы: su=s'u=s"u; q=q1. Т. о., равенство (3) даёт общий вид зависимости между напряжениями и деформациями при произвольном процессе нагружения. Определение функционалов пластичности по данным опытов чрезвычайно затруднительно и пока предложены способы построения лишь части из них.

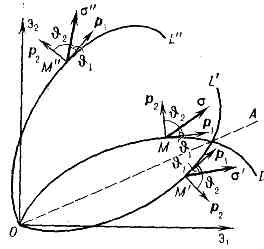Рис. 3. Графики процессов с одинаковой внутренней геометрией k(s).

Другое фундаментальное св-во пластичности изотропного материала отражает принцип запаздывания: значения углов ориентации вектора напряжений в репере Френе зависят от изменения кривизн не на всей предшествующей траектории деформации, а лишь на последней её части, длина к-рой, характерная для данного материала, наз. с л е д о м з а п а з д ы в а н и я. Это св-во позволило выделить неск. типов процессов (простой деформации, малой кривизны, средней кривизны, двухзвенных), для к-рых соотношения между напряжениями и упругопластич. деформациями установлены конкретно и не содержат функционалов.

Т е о р и я т е ч е н и я. Тензор напряжений sij представляется в шестимерном пространстве точкой нагружения N, или вектором напряжений s=ON. В процессе нагружения sij(t) точка N очерчивает траекторию нагружения (рис. 4). Деформация представляется в виде суммы упругой и пластической. Упругая часть деформации связана с напряжениями обобщённым законом Гука. Все напряжённые состояния, к-рые могут быть достигнуты из начального состояния без возникновения пластич. деформаций, располагаются на нек-рой поверхности F, наз. начальной п о в е р х н о с т ь ю т е к у ч е с т и. При выходе точки нагружения N за пределы поверхности F (активный процесс, нагрузка) изменяются величины упругой и пластич. деформации и форма поверхности текучести (процесс NN' и новая, мгновенная поверхность текучести F'). Если затем точка нагружения перемещается внутрь мгновенной поверхности текучести (процесс N'N"), то изменяется только упругая деформация, а пластич. деформация и поверхность текучести процессов.

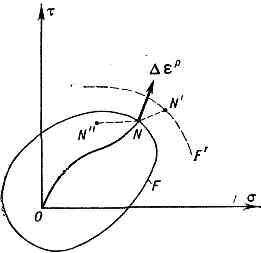Рис. 4. Траектория нагружения ON и поверхности текучести F для активного NN' и пассивного NN" неизменны (пассивный процесс, разгрузка). Конфигурация поверхности текучести явл. функционалом процесса нагружения.

В основе теории течения лежит постулат пластичности, согласно к-рому работа напряжений на замкнутом цикле напряжений (деформаций), не может быть отрицательна, откуда следует, что вектор скорости пластич. деформации ep направлен по нормали к мгновенной поверхности текучести в точке нагружения N. Это приводит к соотношениям:

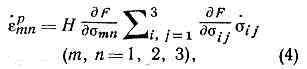где epmn — компоненты тензора пластич. деформации, точками сверху обозначены производные по времени. Т. н. функция упрочнения Н явл. функционалом предшествующего процесса нагружения и зависит от скоростей изменения напряжений. Построить функционал F практически невозможно, поэтому вводятся т. н. гипотезы упрочнения, т. е. упрощающие предположения об изменении поверхности текучести, а соотношения (4) линеаризуют, т. е. пренебрегают зависимостью Н от скоростей напряжений. В таком виде теория течения пригодна для ограниченного класса процессов.

Т е о р и я с к о л ь ж е н и я.

Этим термином объединяется ряд П. т., в к-рых рассматривается поликрист. агрегат (напр., металл). Для описания пластичности отдельного зерна используется одна из простейших теорий пластичности (напр., теория идеальной пластичности), Поликрист. агрегат рассматривается как статистич. ансамбль с равновероятным распределением форм и размеров зёрен, существующих как бы в одной точке, и преимущественных плоскостей скольжений. Условия кинематич. и динамич. контакта между зёрнами учитываются не полностью. Путём статистич. анализа разыскивается связь между напряжениями и деформациями в макрообъёме агрегата.

Математическая П. т. Матем. задача П. т. сводится к разысканию компонентов вектора перемещения, тензора деформации и тензора напряжений как ф-ций координат и времени, к-рые при заданных в объёмах тела массовых силах и темп-ре, усилиях на одной части граничной поверхности и перемещениях на другой части поверхности должны удовлетворять дифф. ур-ниям движения (или равновесия), ур-ниям связи между деформациями и перемещениями, ур-ниям связи между напряжениями деформациями и темп-рой (законам пластичности), граничным и нач. условиям. Система этих ур-ний составляет краевую задачу П. т.

Формулировка матем. задачи П. т. отличается от краевой задачи упругости теории только тем, что соотношения обобщённого закона Гука заменяются соотношениями той или иной П. т. При использовании теории идеальной пластичности (и др. теорий течения) вместо перемещений и деформаций разыскиваются скорости ч-ц и тензор скоростей деформации. При использовании соотношений пластичности, относящихся к частным классам процессов, требуется анализ физ. достоверности решения краевой задачи, т. к. в большинстве случаев не выяснены те условия нагружения тела произвольной формы, при к-рых во всех точках тела протекают процессы деформации определённого типа. В теории упругопластич. процессов дан общий метод установления физ. достоверности решений.

ПЛАСТИЧНОСТИ ТЕОРИЯ

математическая- наука о пластич. деформировании тел. П. т. занимается построением матем. моделей пластич. тел, методами определения напряжений и деформаций в пластическидеформиров. телах. За исходные положения П. т. принимаются эксперим. данные, и непосредственно она не связана с физ. объяснением свойств пластичности. Совр. П. т. в основном связана со свойствами металлов; её применениявозможны к таким материалам, как горные породы, лёд и т. д.
Осн. эксперименты по определению пластич. свойств металлов проводятся при испытании на растяжение - сжатие плоскогоили цшшндрич. образца при однородном деформировании тонкостенной цилиидрич. трубки, находящейся под действием растягивающей силы, крутящего моментаи внутр. давления. На диаграмме напряжение - деформация (рис. 1) при одноосномрастяжении образца мягкой малоуглеродистой стали до точки А деформацииявляются упругими (линейный участок).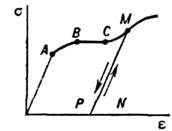

Рис. 1. Диаграмма зависимости напряжение- деформация для образца из мягкой малоуглеродистой стали.

Точка А соответствует пределу пропорциональностиматериала, т. е. макс. напряжению, при к-ром ещё справедлив Гуна закон. Наиб. напряжение, к-рое может выдержать данный материал, не обнаруживаяостаточных деформаций при разгрузке, наз. пределом упругости, или пределомпластичности; он не совпадает с пределом пропорциональности, но обычноих различием в П. т. пренебрегают. После точки А диаграмма становитсякриволинейной, а на отрезке ВС она имеет горизонтальную площадку, наз. площадкой текучести. Точка В соответствует пределу текучестиматериала. На площадке текучести деформация возрастает без увеличения напряжения. Начиная с точки С кривая вновь идёт вверх. Если снять нагрузку, то диаграмма разгрузки оказывается прямой МР, параллельной прямойупругого участка. Полная деформация 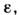соответствующая точке М, состоит из двух частей - упругой 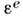ипластической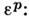

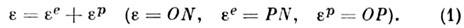
Вторичное приложение растягивающих усилийсопровождается упругим деформированием до достижения растягивающими напряжениямизначений, имевших место в нач. момент разгрузки (прямая РМ), т. о., вторичный вывод материала в пластич. область повышает предел упругости. Это явление наз. упрочением или наклёпом. При сжатии диаграмма напряжение- деформация подобна диаграмме растяжения. Однако наклёп материала прирастяжении понижает предел упругости при сжатии (т. н. Баушингера эффект). При пластич. деформировании возникает анизотропия механич. свойствв разных направлениях и эффект Баушингера - следствие приобретённой пластич. анизотропии.
Эксперименты показывают разнообразие вповедении металлов и др. твёрдых тел при пластич. деформировании. Существеннымоказывается влияние скорости нагружения. При повышенной темп-ре (а в нек-рыхслучаях при комнатной темп-ре) твёрдые тела обнаруживают свойства ползучестии др. последствия. П. т. идеализирует сложное поведение реальных материалов;для разл. областей применения используются разл. модели пластич. тел. Обычнов П. т. диаграмму напряжение - деформация аппроксимируют схемой (рис. 2),состоящей из двух участков: отрезка ОА, соответствующего упругомусостоянию материала, и отрезка АС, соответствующего состоянию пластичности. Широко используется схема жёсткопластического тела, где упругимидеформациями пренебрегают по сравнению с пластическими (рис. 2,в). Выбормодели пластич. тела состоит в установлении связи между тензорами, определяющиминапряжённое и деформиров. состояние материала.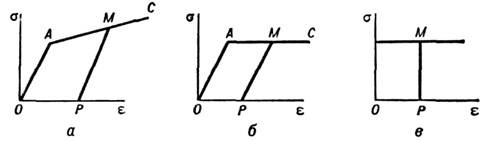

Рис. 2. Идеализированные схемы зависимости -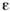: а- упругопластический материал с линейным упрочением; б - идеальныйупругопластический материал; в - идеальный жёсткопластический материал.

При пластич. деформировании напряжённоеи деформиров. состояния материала зависят от последовательности нагружения. Данному напряжённому состоянию могут соответствовать различные пластич. деформации в зависимости от того, какой последовательностью напряжённыхсостояний оно достигнуто.
Теории пластического течения. В теориипластич. течения устанавливается связь между тензором напряжений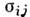 и тензором приращений пластич. деформации 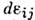(или тензором скоростей пластич. деформаций 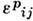).Приращение полной деформации равно сумме приращений упругой и пластич. деформации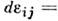 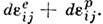Предполагается, что упругая часть деформации 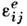связана с напряжениями законом Гука. Теории пластич. течения характеризуютсянеголоном-ным видом связи между напряжениями и деформациями. Термин "течение"в П. т. имеет смысл, отличный от течения, напр., вязких жидкостей: соотношениятеорий пластич. течения не зависят от времени и при фиксиров. нагрузкахизменение деформирования пластич. тел не происходит (в противном случаеимеет место ползучесть материала).
В П. т. используется понятие пространстванапряжений. В шестимерном пространстве напряжений П декартовы координатысоответствуют компонентам тензора напряжений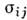 .Любому напряжённому состоянию в пространстве П соответствует вектор напряжений 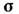с компонентами 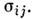В пространстве П определяется поверхность нагружения 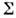,ограничивающая все упругие состояния данного элемента тела (т. е. все состояния, к-рые могут быть достигнуты из начального без приобретения остаточных деформаций).Напряжённые состояния, соответствующие точкам поверхности нагружения 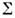,соответствуют пределам текучести при сложном напряжённом состоянии. Приизменении напряжённого состояния поверхность нагружения изменяет свою форму.
Из опыта известно, что материал, находящийсяв любом напряжённом состоянии, можно деформировать, не сообщая ему остаточныхдеформаций (упругая разгрузка). Поэтому поверхность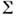 при изменении своей формы меняется так, что всё время проходит через конецвектора напряжении 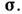Если для нек-рого материала напряжённое состояние меняется от 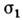до 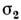(рис. 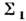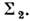3),то поверхность нагружения занимает соответственно положения и Приизменении поверхности нагружения так, как показано на рис. 3( а),увеличение предела текучести в одном направлении приводит к понижению егов противоположном направлении. Если поверхность 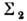включает в себя поверхность 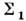(рис. 3,6), то пределы текучести увеличиваются во всех направлениях. При этом поверхность 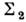можетоставаться гладкой (рис. 3, а, б) или приобретать угл. точку.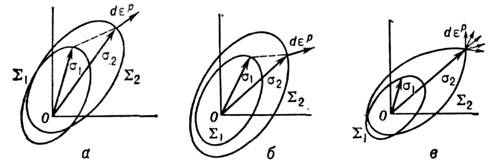

Рис. 3. Изменение поверхности нагруженияпри изменении напряжённого состояния от 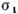до 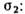а и б - поверхности нагружения остаются гладкими;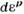- вектор приращения пластич. деформации (ортогональный к поверхности нагружения, согласно ассоциированному закону); в- поверхность нагружения приобретаетугловую точку, стрелки ограничивают возможные направления вектора приращенияпластической деформации (согласно обобщённому ассоциированному закону пластическоготечения).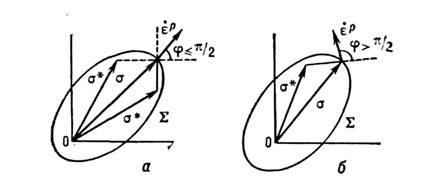

Рис. 4. а - вектор 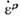ортогонален к поверхности нагружения; для любых 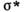неравенство Мизеса выполняется: угол между векторам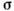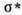и - и 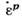меньше или равен 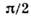; б- вектор 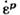неортогонален к поверхности нагружения. Найдётся такое 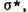при котором неравенство Мизеса не выполняется; угол между векторам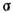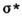и - и 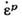больше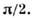

Аналитич. выражение поверхности нагруженияможно записать в виде f = 0. Ф-ция f наз. ф-цией нагруженияи может зависеть от компонент напряжений, пластич. деформаций, разл. параметров, связанных с процессами нагружения неголономными дифференциальными или функциональнымисоотношениями, и др.
Соотношения связи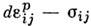 формулируются обычно на основе принципа (постулата) максимума Мизеса: дляфиксиров. точки поверхности 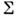и действит. компонент скорости пластич. деформации 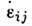имеет место неравенство 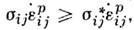где 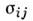- компоненты действительного напряжённого состояния, а 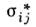- компоненты любого возможного напряжённого состояния, т. е. лежащего внутриили на поверхности 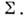Из принципа Мизеса следуют невогнутость поверхности нагружения и ассоцииров. закон течения, определяющий ортогональность вектора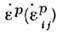
и поверхности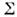 (рис. 4).
Аналитич. выражение связи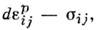 определяемое ассоцииров. законом пластич. течения, имеет вид

где f - ф-ция нагружения, к-раяв этом случае наз. пластическим потенциалом. Для поверхности нагруженияс особенностями (угл. точки, рёбра и т. п.) имеет место теория обобщённогопластич. потенциала и обобщённого ассоцииров. закона течения.
В основу построения П. т. наряду с определениемф-ций нагружения и принципом Мизеса, согласно к-рому варьируются компонентынапряжения (статич. подход), возможно построение П. т., исходящее из определениядиссипативной ф-ции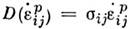 и принципа Онсагера, при к-ром варьируются компоненты скорости пластпч. деформации (кинематич. подход). Оба подхода построения П. т. эквивалентны.
Теория идеальной пластичности. В П. т. наиб. развита теория идеальной пластичности. Для идеального пластич. телаповерхность нагружения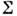 фиксирована, в этом случае 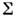наз. поверхностью пластичности или текучести. Ур-ние поверхности пластичности(текучести) имеет вид 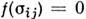и наз. условием пластичности (текучести). Соотношение плоской задачи теорииидеальной пластичности даны А. Сен-Венаном (A. Saint-Venant, 1871), использовавшимусловие пластичности макс, касательного напряжения: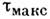=k,где k - константа материала. В этом случае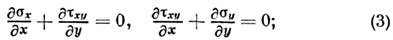

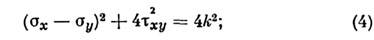
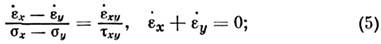
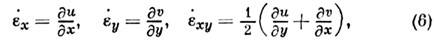
где (3) - ур-ния равновесия; (4) - условиепластичности; (5) - условие изотропии, утверждающее совпадение гл. осейтензоров напряжений и скоростей пластич. деформаций; условие несжимаемости;(6) - ф-лы Коши, связывающие компоненты скорости деформации с компонентамискорости перемещений и, v. Характерной особенностью является замкнутостьсистемы трёх ур-ний (3 и 4) относительно трёх неизвестных компонент напряжений 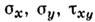. В этом смысле задача является статически определённой. Ур-ния (3 и 4)принадлежат к гиперболич. типу, ортогональные характеристики совпадаютс линиями скольжения (линии разрыва скоростей перемещений), наблюдаемымиэкспериментально.
В теории идеальной пластичности нарядус условием макс. касательного напряжения используются разл. условия пластичности.
Построение теории идеальной пластичностив общем случае с единым матем. аппаратом (ур-ния гиперболич. типа) имеетместо при использовании условия пластичности макс. касательного напряженияи обобщённого ассоцииров. закона пластич. течения.
Для ребра призмы Треска, интерпретирующейв пространстве напряжений пластичности условие Треска, пмеет местовыражение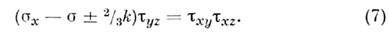

Система шести ур-ний: трёх ур-ний равновесияи трёх ур-ний (7) [недостающие два получаются из (7) круговой перестановкойиндексов ( х у z)] относительно шести неизвестных компонент напряжений 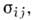как и в плоском случае, является статически определимой.
Согласно теории обобщённого пластич. потенциала, любое деформиров. состояние может соответствовать ребру призмы Треска.
На основе модели идеально-пластическоготела развиты теории технол. задач обработки металлов давлением, несущейспособности конструкций оптимального проектирования, приспособляемости, динамики упругопластич. и жёсткопластич. тела и др.

Модели пластических сред. Обобщениемтеории идеальной пластичности для упрочняющегося материала является теориятрансляц. упрочнения (А. Ю. Ишлинский), согласно к-рой происходит смещениеповерхности пластичности как твёрдого целого в пространстве напряженийв зависимости от роста пластич. деформаций:

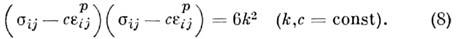
Компоненты 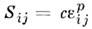в (8) могут интерпретироваться как внутр. упругие микронапряжения. Теориятрансляц. упрочнения описывает аффекты приобретённой анизотропии и связанныйс ней эффект Баушингера.
Существуют разл. подходы к описанию поведенияупрочняющихся пластич. тел. Теории скольжения рассматривают материал какполикристаллич. агрегат с равновероятным распределением форм и размеровзёрен в элементарном объёме тела, в к-ром выделяются преимуществ. линиискольжения. Вклад отд. поверхностей скольжения в пластич. деформированиеопределяется в нек-рой интегральной форме. Подобные теории могут быть описаныв рамках теории обобщённого пластич. потенциала.

Деформационные теории пластичности. При активном простом (пропорциональном) нагружении соотношения теориималых упругопластич. деформаций (А. А. Ильюшин, 1943) имеют вид

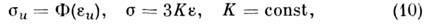
где

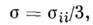
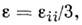
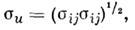
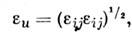
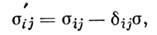
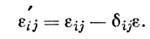
Согласно (9), векторы девиаторов напряжений и девиатарое деформаций коллинеарны. Соотношения (10) определяютфункциональную зависимость модулей этих векторов, пропорциональность измененияобъёма среднему давлению.
Сравнит. простота соотношений теории малыхупругопластич. деформаций позволила получить ряд важных результатов прирасчётах на прочность и устойчивость деталей конструкций (труб, стержней, пластин, оболочек), дать методы определения динамич. напряжений при продольномударе стержней и т. д.

Теории упругопластических процессов. В теории сложного непростого, непропорционального нагруже-ния (Ильюшин)аналогично пространству напряжений вводится пятимерное пространство девпаторадеформаций 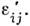В процессе деформирования вектор девиатора деформации описывает кривую, наз. траекторией деформации, внутр. геометрия к-рой описывается четырьмякривизнами k_i, определяющими т. н. репер Френе, и пятьюединичными векторами р _i.
Параметрами, характеризующими процессдеформации, являются: ориентация траектории, её внутр. геометрия (кривизна),скорость деформации, др. механич. и термодинамич. параметры, заданные какф-ции длины дуги. Вектор напряжений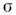 определяется модулем 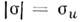и углами ориентации :

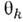Для определения соотношений связи (11)устанавливают зависимость величин 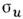, 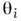(где .= 1,..., 5) от параметров произвольного процесса деформации.
Согласно постулату изотропии, для изотропногоматериала модуль вектора напряжений и углы его ориентации в репере Френеоднозначно определяются изменением параметров процесса от его начала дотекущего момента, т. е. они являются функционалами, порождаемыми ф-циями k_i и др. параметров. Полное определение функционаловпластичности по данным опыта чрезвычайно затруднительно, и пока предложеныспособы построения лишь части из них.
Другое свойство пластичности изотропногоматериала отражает принцип запаздывания: значения углов ориентации векторанапряжений в репере Френе зависят от изменения кривизны не на всей предшествующейтраектории деформации, а на последней её части, длина к-рой, характернаядля данного материала, наз. следом запаздывания. Это свойство позволиловыделить неск. типов процессов (простой деформации, малой кривизны и т. п.), для к-рых соотношения между напряжениями и упругопластич. деформациямиустановлены конкретно и не содержат функционалов.
Идеи теории упругопластич. процессов реализуютсяв т. н. эндохронных теориях, использующих зависимости напряжения - деформациив виде функционала.

Лит.: Соколовский В. В., Теорияпластичности, 3 изд., М., 1969; Прагер В., X о д ж Ф., Теория идеальнопластических тел, пер. с англ., М., 1956; Xилл Р., Математическая теорияпластичности, пер. с англ., М., 1956; Кадашевич Ю. И., Новожилов В. В.,Теория пластичности, учитывающая остаточные микронапряжения, "ПММ", 1958,т. 22, с. 78; Ильюшин А. А., Пластичность. Основы общей математическойтеории, М., 1963; Ивлев Д. Д., Быковцев Г. И., Теория упрочняющегося пластическоготела, М., 1971; Ревуженко А. Ф., Чанышев А. И., Шемякин Е. И., Математическиемодели упругопластических тел, в сб.: Актуальные проблемы вычислительнойматематики и математического моделирования, Новосиб., 1985.

Д. Д. Ивлев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.