THERMIQUE
La thermique est la branche de la physique qui traite des échanges de chaleur accompagnés ou non d’échange de masse et de changement de phases. Elle peut donc être considérée comme partie intégrante de la thermodynamique des phénomènes irréversibles puisque, pour avoir l’échange de chaleur entre différentes parties d’un système, il est nécessaire que ce système soit en dehors de l’équilibre thermodynamique [cf. THERMODYNAMIQUE].
Il a fallu longtemps pour que l’on puisse distinguer entre les divers types d’échanges de chaleur et les classer en rayonnement, conduction, convection naturelle et convection forcée. D’ailleurs ne parle-t-on pas encore de «radiateurs» de chauffage central ou d’automobile, bien qu’une partie importante du flux de chaleur soit transmise à l’atmosphère par convection naturelle dans le premier cas et par convection forcée dans le second?
Le phénomène de la conduction de la chaleur existe dans tous les corps, solides ou fluides, bien que, pour ces derniers, le transfert d’enthalpie dû à la présence d’un écoulement ait tendance à masquer le phénomène de conduction. Celui-ci se traduit par une élévation de température de proche en proche qui, pour les solides, correspond à un accroissement de l’énergie de vibration du réseau cristallin et, pour les fluides, à une transmission d’énergie cinétique opérée par les chocs entre les molécules. C’est à J. Fourier (1822) que l’on doit la théorie analytique de la conduction de la chaleur qui a amené, en dehors des applications physiques, à des progrès en analyse mathématique (cf. équations aux DÉRIVÉES PARTIELLES, SÉRIES TRIGONOMÉTRIQUES).
Dans les fluides, l’existence d’un champ de températures non uniforme modifie localement la masse volumique de ces fluides et entraîne, dans un champ de forces volumiques (pesanteur, force centrifuge), des mouvements dits de convection naturelle. Ces mouvements ont été étudiés pour la première fois par H. J. E. Bénard (1901) entre deux plaques horizontales à températures différentes. Ils existent également dans des couches limites au voisinage de corps chauffés ou refroidis et impliquent un transport de chaleur plus important que la simple conduction.
Si le fluide caloporteur est entraîné artificiellement, le flux de chaleur, dit de convection forcée, augmentera avec la vitesse de ce fluide, et les gradients de température seront plus élevés dans une couche limite thermique analogue à la couche limite dynamique introduite par L. Prandtl. Si la vitesse d’entraînement n’est pas très élevée, les deux processus de convection naturelle et de convection forcée peuvent coexister: c’est la convection mixte.
Le rayonnement thermique est connu depuis la plus haute antiquité, dès que les hommes ont remarqué la possibilité de rôtir les viandes sans les enfumer en les disposant devant les braises incandescentes, dans le courant d’air froid, au lieu de les placer au-dessus de celles-ci, dans le courant d’air chaud; c’est également le rayonnement des parois portées à haute température qui assure la cuisson du pain dans le four.
Par contre, les lois scientifiques du rayonnement ne se sont dégagées que très tardivement: si l’on met à part la loi «géométrique» de Lambert, donnant la distribution dans l’espace de l’énergie du rayonnement thermique d’un élément de surface, qui remonte à 1760 et qui semble avoir été pressentie (sinon explicitement formulée) par Kepler dès le début du XVIIe siècle, toutes les lois du rayonnement thermique ont été découvertes à partir de la fin du XIXe siècle. En 1879, J. Stefan découvre expérimentalement que l’énergie totale émise par un élément de surface est proportionnelle à la quatrième puissance de sa température; cinq ans plus tard, L. Boltzmann en donne l’explication théorique; l’analyse spectrale du rayonnement thermique ne commence que vers 1895, époque où J. W. Rayleigh et W. Wien établissent des formules plus ou moins empiriques donnant une répartition de l’énergie émise en fonction de la longueur d’onde et de la température; à la même époque, G. R. Kirchhoff énonce une loi établissant une relation entre la puissance émise par un corps dans une longueur d’onde particulière et l’absorption de ce corps pour la même longueur d’onde, caractérisant ainsi une qualité de rayonnement des corps par rapport au corps noir totalement absorbant et totalement émetteur.
À ce stade, toutes les manifestations extérieures du rayonnement thermique étaient ainsi assez bien connues, mais le mécanisme physique de ce rayonnement restait presque totalement ignoré. Le mérite revient à M. Planck d’avoir ouvert la voie à une compréhension approfondie non seulement du rayonnement thermique, mais de bien d’autres phénomènes physiques: c’est en effet pour rendre compte de l’existence d’un maximum dans la répartition spectrale de l’énergie rayonnée que Planck a été amené à supposer des échanges énergétiques discontinus, inaugurant ainsi les fructueuses théories quantiques et la physique corpusculaire, sans laquelle les mécanismes du rayonnement thermique ne pourraient être compris (cf. mécanique QUANTIQUE).
D’une manière générale, les applications de la thermique comprennent tous les procédés de transmission et d’utilisation de la chaleur, à l’exception de ceux qui dérivent des lois de la thermodynamique et de la thermochimie reliant les phénomènes calorifiques aux phénomènes mécaniques et chimiques.
1. Le rayonnement thermique
Lois fondamentales
On entend par rayonnement non corpusculaire toute forme d’énergie susceptible de se transmettre à travers le vide; toutes les ondes électromagnétiques, depuis les rayons 塚 et cosmiques dont les longueurs d’onde sont inférieures au dixième de micromètre jusqu’aux ondes radio pour lesquelles elles atteignent plusieurs kilomètres, constituent des rayonnements non corpusculaires.
La luminance
Le rayonnement thermique est caractérisé non par sa nature physique mais par son origine: il est spécifiquement lié à la température du corps émetteur (solide, liquide, gaz) et se distingue ainsi nettement des luminescences, dues à des phénomènes physico-chimiques ou électriques qui sont également des rayonnements [cf. LUMINESCENCE]. Il se distingue moins nettement du rayonnement émis par les flammes de combustion ou les explosions gazeuses dans lesquelles se produisent des réactions physico-chimiques mais où des gaz et, éventuellement, des particules solides portés à de hautes températures peuvent émettre également un rayonnement thermique.
Tout corps chauffé émet un rayonnement, qui peut être visible, la surface du corps prenant alors une coloration plus ou moins vive, ou invisible, la surface du corps ne changeant pas alors d’aspect mais donnant à distance une sensation de chaleur ou impressionnant certaines pellicules photographiques.
On observe facilement que la sensation de chaleur due à un élément de surface chauffé est maximale sur la perpendiculaire N à cet élément et nulle dans son plan (dans la mesure où le rayonnement de toute surface latérale a été éliminé); plus précisément, l’énergie d 2 淋 rayonnée par l’élément d S dans un pinceau issu du centre O de d S et découpant une aire d 行 (angle solide) sur la sphère de rayon unité centrée en O est proportionnelle au produit d S d 行 et au cosinus de l’angle de la perpendiculaire N avec la direction moyenne du pinceau, selon la formule:
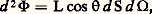
où le coefficient L est, par définition, la luminance du corps.
La loi de Lambert
Si l’on étudie l’énergie correspondant à une radiation de longueur d’onde déterminée, isolée de l’ensemble des radiations constituant le rayonnement, la luminance L dépend de la nature du matériau constituant l’élément d S, de sa température T et de la longueur d’onde de la radiation; si L ne dépend pas de l’angle , on dit que la surface du matériau considéré suit la loi de Lambert; ce qui est approximativement le cas de nombreux corps électriques isolants mais non celui des métaux polis. Le rayonnement de ces derniers est, en effet, forcément polarisé, c’est-à-dire qu’il présente une répartition d’énergie très inégale entre les vibrations parallèles et les vibrations perpendiculaires à d S: seules les premières suivent à peu près la loi de Lambert, et la théorie permet de prévoir que la luminance augmente au contraire avec l’angle . En pratique, cette théorie n’est plus valable pour les valeurs de voisines de 900 et, de plus, la moindre trace d’oxydation du métal poli modifie considérablement sa luminance et réduit l’écart à la loi de Lambert. Signalons encore qu’un même matériau peut suivre la loi de Lambert dans une certaine gamme de longueurs d’onde et ne pas la suivre dans une autre gamme.
La loi de Kirchhoff
L’influence du matériau sur l’énergie rayonnée est définie par la loi de Kirchhoff, qui introduit l’émissivité 﨎 du matériau. On ne peut dissocier ce facteur d’émission des caractéristiques du comportement du même matériau quand il est soumis à un rayonnement extérieur: quand un rayonnement monochromatique d’énergie 淋 tombe sur l’élément d S, une partie 精淋 de l’énergie incidente est transmise à travers le corps, une partie 見淋 est absorbée par lui et une partie 福淋 est réfléchie; les trois coefficients 精, 見 et 福 (transmitivité, absorptivité, réflectivité) sont liés par la relation:
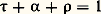
exprimant le principe de conservation de l’énergie.
Pour un corps opaque, c’est-à-dire totalement absorbant, on a 精 = 0; pour un corps noir, c’est-à-dire à la fois opaque et non réfléchissant, on a 精 = 0 et 福 = 0, de telle sorte que 見 = 1; pour le corps blanc, au contraire, 見 est nul. Ces trois sortes de corps sont évidemment des cas limites, mais on observe que les corps les plus absorbants sont aussi les plus thermiquement émissifs; c’est pourquoi le corps noir est pris comme élément de comparaison et de référence pour le rayonnement des corps quelconques, dont l’émissivité est, par définition, le rapport (inférieur à 1) de leur énergie rayonnée à l’énergie rayonnée dans la même longueur d’onde par le corps noir porté à la même température. Parmi eux, les corps gris ont une émissivité indépendante de la longueur d’onde.
La loi de Kirchhoff pose:

c’est-à-dire que l’émissivité d’un corps est égal à son absorptivité; cette loi est bien vérifiée en pratique à condition que le rayonnement considéré soit purement thermique et que le corps ne soit pas investi d’un milieu ambiant, gazeux ou liquide, présentant un trop grand déséquilibre thermique avec lui: de récentes recherches sur les effets d’environnement laissent penser, en effet, que ces deux coefficients peuvent être assez différents quand la température du corps émetteur et celle du gaz ambiant sont très éloignées l’une de l’autre.
Tous les coefficients introduits à propos de cette loi sont pratiquement indépendants de la température du corps mais sont fortement liés à la longueur d’onde. Cette sélectivité de la transmission, de l’absorption, de la réflexion et de l’émission n’est pas sans intérêt pratique, car elle permet de réaliser, par exemple, un éclairage naturel suffisant des locaux habités sans échauffement excessif et, au contraire, un chauffage solaire ou artificiel utilisant les radiations les plus chaudes du spectre. Il en résulte que certains corps dont l’émissivité est voisine de 1 pour certaines longueurs d’onde sont quasi noirs pour cette partie du spectre; c’est en particulier le cas des oxydes réfractaires pour les longueurs d’onde de 6 à 8 猪m (infrarouge); la réalisation d’un corps noir parfait est évidemment impossible, mais on peut l’approcher de près en pratiquant une ouverture dans une enceinte de grandes dimensions par rapport à celles de l’ouverture, à l’intérieur de laquelle tout rayon subit de nombreuses réflexions sans pouvoir sortir. Un tel corps noir est en fait un véritable piège à rayonnements.
L’émissivité est généralement très influencée par l’état de la surface et des couches moléculaires situées immédiatement en dessous de celle-ci. Cet état est modifié non seulement par le mode d’usinage ou par les traitements chimiques superficiels, mais aussi par d’éventuelles évolutions antérieures du corps, ce qui impose de faire subir à tout échantillon servant à déterminer un facteur d’émission un traitement équivalent à celui de l’objet auquel il sera appliqué.
Lois du corps noir
Formule de Planck
L’introduction de l’émissivité 﨎 permet d’écrire l’énergie rayonnée par un corps gris sous la forme:

où L0 est la luminance du corps noir; le coefficient 﨎 dépend de la longueur d’onde mais non de la température, tandis que L0 dépend de l’un et de l’autre, et c’est l’étude de la fonction L0(, T) qui a conduit Planck à sa quantification des échanges énergétiques [cf. PLANCK (M.)].
La base de la théorie quantique est l’hypothèse selon laquelle les états énergétiques relatifs à un oscillateur harmonique de fréquence 益 ne peuvent être que des multiples entiers du quantum h 益 (la constante de Planck h vaut 6,624 憐 10 size=1漣34 J 練 s). On démontre d’abord que le nombre des états vibratoires de fréquences comprises entre 益 et 益 + d 益 est donné, pour un volume V, par:
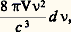
où c désigne la vitesse de la lumière (2,998 憐 108 m 練 s size=1漣1); la fréquence étant liée à la longueur d’onde par la relation 益 = c /, ce nombre est également donné par la fonction analogue de la longueur d’onde:

Il faut alors introduire l’énergie moyenne d’un oscillateur de fréquence 益: le principe classique de l’équipartition de l’énergie donnerait uniformément k T pour toutes fréquences, k étant la constante de Boltzmann (1,381 憐 10 size=1漣23 J 練 K size=1漣1), et T la température du système; la luminance du corps noir serait alors:

d’après la formule de Rayleigh-Jeans , et augmenterait indéfiniment avec la fréquence, ce que contredit l’expérience; c’est ici qu’interviennent les valeurs quantiques h 益, 2 h 益, 3 h 益, etc., dont l’énergie moyenne est déduite en affectant à chaque valeur ph 益 le facteur exp (face=F0019 漣 ph 益/k T) donné par la mécanique statistique classique. On obtient ainsi, pour la luminance monochromatique L0 relative aux états vibratoires de fréquences comprises entre 益 et 益 + d 益, l’expression:
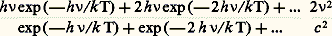
dont le numérateur et le dénominateur s’expriment facilement sous forme finie, et on obtient ainsi la formule de Planck qui s’écrit, en fonction de la longueur d’onde, sous la forme:

Lois de Wien
La luminance L0 présente bien le maximum observé expérimentalement pour une longueur d’ondem définie par la relation:

qui s’explicite parm T = 2,897 K 練 猪m et constitue une première loi de Wien: le produit de la température par la longueur d’onde de la radiation d’énergie maximale correspond à une luminance L0m qui s’obtient immédiatement sous la forme:

avec C=4,071 憐10 size=1漣6 W 練m size=1漣3 練sr size=1漣1 練K size=1漣5, et exprime une seconde loi de Wien : la luminance monochromatique maximale est proportionnelle à la cinquième puissance de la température. Ces deux lois avaient été obtenues par Wien, avant l’élaboration de la formule de Planck, par des raisonnements de thermodynamique classique ingénieux mais aussi assez laborieux.
Loi de Rayleigh-Jeans
Pour les grandes valeurs de T, l’exponentielle figurant au dénominateur de L0 peut être approchée par le développement du premier ordre (1 + hc /kT), ce qui donne à L0 l’expression:

équivalente à celle de Rayleigh-Jeans ci-dessus. Le principe classique de l’équipartition de l’énergie se présente ainsi comme une approximation de la théorie quantique de Planck.
Loi de Stefan-Boltzmann
Enfin, une dernière loi, également obtenue directement par des raisonnements de thermodynamique classique, peut être déduite de la formule de Planck; c’est celle de Stefan-Boltzmann, qui donne la luminance totale en fonction de la température: on l’obtient ici en intégrant simplement la luminance monochromatique sur toutes les longueurs d’onde, et il vient ainsi:
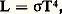
avec 靖 = 5,674 憐 10 size=1漣8 W 練 m size=1漣2 練 K size=1漣4: la luminance totale du corps noir est proportionnelle à la quatrième puissance de la température.
Mécanisme physique du rayonnement thermique
L’analogie parfaite que présente le comportement des rayonnements thermiques avec celui des autres rayonnements électromagnétiques (les ondes radio en particulier) suggère que l’émission du rayonnement thermique est produite par un mécanisme du type oscillateur, et celui-ci est nécessairement composé de particules constituant le matériau émissif. Ce mécanisme est en fait d’une nature assez différente selon que le rayonnement thermique est émis par un corps opaque ou transparent, par un solide conducteur, un solide non conducteur ou un gaz. Pour comprendre ces divers mécanismes, il est plus aisé d’analyser l’absorption de ces différents milieux que leur émission, et l’on peut légitimement penser que ces deux phénomènes ne sont que les deux aspects complémentaires d’une même réalité physique, car la loi de Kirchhoff de l’égalité des deux facteurs est vérifiée dans toutes les observations faites dans les conditions convenables.
Corps opaques et corps transparents
On est ainsi amené à étudier la propagation d’une onde électromagnétique dans le milieu émetteur; si ce dernier est opaque, la transmitivité 精 est nulle et l’émissivité 﨎 vaut 1 漣 福; si au contraire le milieu est transparent, la réflectivité 福 est nulle et le facteur 﨎 est égal à 1 漣 精; on voit ainsi apparaître une différence fondamentale entre ces deux comportements limites: le premier est localisé à la surface du corps, tandis que le second est réparti dans toute l’épaisseur du milieu. L’absorption est généralement une fonction exponentielle de l’épaisseur x de la forme 1 漣 exp[ 漣 k ()x ], et le produit kx est appelé épaisseur optique du milieu .
Conducteurs et non-conducteurs
Une autre différence fondamentale est observée entre l’absorption d’un corps conducteur et celle d’un corps non conducteur: le conducteur absorbe les ondes électromagnétiques de toutes longueurs d’onde, alors que le non-conducteur présente une absorption sélective portant sur des longueurs d’onde données.
Il est ainsi logique de relier le facteur d’émission d’un corps à sa conductibilité électrique; il ne peut être question de présenter ici les calculs complexes ni même les formules exprimant cette relation. Signalons simplement la parfaite concordance, pour les corps non conducteurs, entre les longueurs d’onde d’absorption calculées et celles qui sont observées; il y a également une concordance satisfaisante pour les facteurs d’émission.
Pour les corps conducteurs, la confrontation n’est satisfaisante que pour des températures modérées et des longueurs d’onde assez grandes (supérieures à environ 4 猪m); les divergences, assez notables, observées dans les autres domaines, font encore l’objet de travaux d’interprétation et de correction.
Rayonnement des gaz
La plupart des gaz monoatomiques ou polyatomiques symétriques (A, H2, 2, 2) n’absorbent aucun rayonnement, visible ou invisible, et sont appelés gaz non lumineux ou gaz clairs, car ils n’émettent aucun rayonnement thermique. En revanche, les gaz polyatomiques non symétriques (CO2, H2O, 2O) présentent des absorptions sélectives et, corrélativement, des émissions de rayonnements de longueurs d’onde déterminées (spectres de raies). Malgré la ressemblance avec le rayonnement thermique d’un solide non conducteur, le mécanisme du rayonnement des gaz est très différent, et l’observation ci-dessus conduit à relier ce mécanisme au modèle moléculaire. Pour une molécule diatomique telle que CO, le modèle est relativement simple et peut se réduire à deux sphères inégales liées l’une à l’autre par une force de rappel; l’énergie d’une telle molécule comprend, d’une part, l’énergie de vibration de la distance mutuelle des deux sphères et, d’autre part, l’énergie de rotation de l’ensemble des deux sphères autour de leur centre de gravité: si ces énergies sont quantifiées, elles ne peuvent prendre qu’un ensemble discret de valeurs, et tout passage d’un état énergétique E à un état E s’accompagne de l’absorption ou de l’émission d’un photon de fréquence 益 = (E 漣 E)/h . La prévision des fréquences (ou des longueurs d’onde) émises revient donc à la définition de toutes les transitions EE possibles; elles sont maintenant assez bien connues, mais non sans peine, car, bien que certaines transitions soient interdites, elles sont très nombreuses.
Échanges thermiques par rayonnement
Le rayonnement thermique d’un corps dans le vide constitue une perte d’énergie égale à 﨎靖Ts 4 qui se traduit pratiquement par un abaissement de la température Ts du corps: c’est, pour un véhicule spatial, un mode de refroidissement d’une efficacité non négligeable et des plus économiques. Il ne faut pas perdre de vue cependant qu’un élément de surface émissive est rarement isolé dans le vide et que, généralement, il se produit un échange thermique par rayonnement soit avec le milieu ambiant, soit avec d’autres éléments de surface, et, dans ce dernier cas, il faut éventuellement tenir compte de l’absorption du milieu interposé entre les deux éléments de surface considérés.
Échanges avec le milieu ambiant
Le milieu ambiant est un corps transparent, au moins sélectivement; c’est le plus souvent un gaz d’épaisseur finie (fours) ou infinie (atmosphère) dans lequel la température n’est pas toujours uniforme: chaque couche isotherme à la température T émet un rayonnement qui n’obéit pas à la loi de Stefan-Boltzmann, mais, en même temps, elle absorbe une partie du rayonnement émis par les autres couches; il faudra donc intégrer sur toute l’épaisseur ce double effet pour déterminer le flux d 淋g que l’élément d S de surface reçoit effectivement du gaz ambiant et qui viendra réduire son refroidissement par rayonnement. L’intégration est d’autant plus difficile qu’elle fait intervenir des températures qui ne sont pas toujours connues; c’est pourquoi on écrit pratiquement d 淋g sous la forme:

en définissant une émissivité apparente 﨎g , une température moyenne Tg d’un corps gris équivalent au gaz et un coefficient d’absorption 見gs .
Échanges entre éléments de surface
Pour que deux éléments de surface d S et d S de luminances L et L centrés en O et O et perpendiculaires aux vecteurs ね et ね , orientés du côté rayonnant, échangent de l’énergie par rayonnement, il faut qu’ils soient visibles l’un pour l’autre (fig. 1), c’est-à-dire que les vecteurs ね et ね forment respectivement avec les vecteurs のO の O des angles 見 et 見 aigus.
Dans ces conditions, l’échange thermique entre les deux éléments par rayonnement est donné par la relation:

Quand deux surfaces finies S et S possèdent une luminance uniforme, l’échange thermique Q s’exprime sous la forme E(L 漣 L ); le coefficient E, défini par la double intégration:

est purement géométrique et appelé fonction géométrique d’échange. En pratique, il est avantageux d’utiliser les facteurs de forme f SS size=1 et f S size=1S reliés à E par les relations:

qui font apparaître une relation de réciprocité entre ces deux facteurs; ils jouissent, en outre, d’une relation d’addivité:
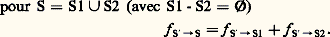
Ces relations permettent d’éviter, pour les configurations géométriques assez simples, une double intégration rendue généralement laborieuse par sa limitation aux portions donnant effectivement lieu à des échanges radiatifs. Ainsi, pour deux sphères, chaque élément d S de centre O de l’une n’échange de rayonnement avec l’autre que dans un cône de sommet O circonscrit à celle-là, la surface effective de S étant elle-même limitée par le cône circonscrit commun aux deux sphères.
La formule précédente suppose qu’aucun milieu absorbant ne s’interpose entre les deux éléments, sinon il y aura lieu d’introduire pour chaque surface un flux d 淋g du type décrit précédemment; lorsque chacune des deux surfaces est à une température approximativement uniforme, on définit quelquefois une épaisseur équivalente du milieu intermédiaire par le rapport, généralement affecté d’un coefficient correctif (V/S) du volume de ce milieu à la plus grande des surfaces rayonnantes: cette épaisseur est purement géométrique, par compensation partielle de l’absorption du gaz et de son rayonnement, l’échange entre les surfaces n’est parfois que peu altéré par la présence du milieu intermédiaire qui peut alors être considéré comme optiquement mince.
La possibilité de refroidissement par rayonnement d’un véhicule spatial a été signalée au début de ce paragraphe. Quant au rayonnement solaire, bien qu’il ne soit pas rigoureusement un rayonnement thermique, il peut cependant être approximativement assimilé à celui d’un corps noir dont la température serait environ de 5 800 K. Ce rayonnement, qui parcourt 150 millions de kilomètres, est fortement absorbé par l’atmosphère terrestre dont l’épaisseur réduite (c’est-à-dire correspondant à des gaz aux conditions normales de température et de pression) est d’environ 8 kilomètres; la conversion directe de l’énergie solaire est ainsi beaucoup plus efficace sur un satellite que sur la surface du globe, et elle est couramment utilisée pour l’alimentation des appareils de mesure, de pilotage et, éventuellement, de survie des occupants, l’énergie solaire, source de la vie terrestre, étant aussi celle de la survie extraterrestre de l’être humain.
2. La conduction
Le processus de conduction de la chaleur s’effectue de proche en proche, la chaleur passant spontanément des corps les plus chauds aux corps les plus froids, la température tendant alors à s’uniformiser lorsqu’il n’y a pas de source de chaleur interne.
Loi de Fourier
Le flux de chaleur à travers une surface est, par définition, la quantité de chaleur (mesurée en joules dans le système SI, cf. MESURE Mesures thermiques) qui traverse, par unité de temps (la seconde), cette surface. La densité de flux de chaleur﨏; en un point est le rapport du flux de chaleur passant à travers un élément de surface entourant ce point à l’aire de cet élément. Cette densité est proportionnelle (pour un corps isotrope) et opposée au gradient de température au point considéré:

c’est la loi de Fourier, étant le coefficient de conductibilité thermique ou conductivité thermique .
Pour les corps anisotropes, tels que les cristaux ou les corps composites (bois, fibres enrobées, milieux poreux), la loi de Fourier se généralise sous forme tensorielle:

La densité de flux de chaleur est le produit contracté d’un tenseur de conductivité thermique et du gradient de température. Pour les corps composites, l’élément de surface qui entre dans la définition de la densité de flux de chaleur ne doit pas être trop petit. La loi correspondant à l’expression (2) n’est valable que pour les grandeurs dont on prend la moyenne dans un volume élémentaire; les dimensions de celui-ci doivent être de l’ordre de grandeur de plusieurs dimensions des éléments des corps composites: les diamètres des fibres pour les fibres enrobées ou les diamètres des pores pour les milieux poreux.
Équation de conservation de l’énergie
La loi de Fourier s’emploie dans le cas d’un solide ou d’un fluide au repos par rapport à un référentiel donné. Par rapport à ce dernier, le premier principe de la thermodynamique donne en chaque point l’équation de conservation de l’énergie [cf. THERMODYNAMIQUE]. Comme, en conduction pure, le travail est nul, si l’on néglige la dilatation thermique, on a:

où h est l’enthalpie massive, t le temps, 福 la masse volumique et q la source (ou le puits) de chaleur provoquée par effet Joule, par frottement interne, par des réactions chimiques ou nucléaires, par absorption de rayonnements lumineux, électromagnétiques ou corpusculaires.
On fait apparaître la température absolue T dans l’équation (3) sous la forme suivante, qui est la plus générale:

où cp est la chaleur massique à pression constante du corps conducteur.
Dans le cas d’un corps isotrope et homogène et sans sources de chaleur internes, l’équation (4) devient:

Si les variations de température sont suffisamment faibles pour que l’on puisse admettre que, normalement fonction de la température, ne varie pratiquement pas, on aura alors une équation appelée équation de la chaleur dans les ouvrages de mathématiques:

où a =/ 福cp est appelée diffusivité thermique .
Pour résoudre l’équation générale (4) ou les équations plus simples (5) et (6) dans le domaine de l’espace occupé par le corps conducteur de la chaleur, il faut s’imposer une condition initiale (en général, la distribution initiale de la température) et des conditions aux limites à la surface du corps conducteur, conditions que l’on classe en trois types principaux:
– distribution de température imposée (variable ou non dans le temps) ou condition de Dirichlet;
– distribution imposée de densité de flux de chaleur (variable ou non dans le temps) ou condition de Neumann;
– relation entre la densité de flux de chaleur à la surface du corps et la température au même endroit. Si cette relation est linéaire, on appelle cette condition la condition de Fourier.
À la limite entre deux corps conducteurs homogènes, on doit avoir les deux conditions suivantes:
– égalité des températures en chaque point de cette limite;
– égalité des composantes normales des densités de flux de chaleur.
Ces deux conditions entraînent une réfraction des lignes de flux de chaleur qui sont les lignes tangentes en tout point à la densité de flux de chaleur (c’est-à-dire, pour un corps isotrope, tangentes au gradient de température et donc orthogonales aux surfaces isothermes sur lesquelles la température est uniforme).
La première de ces deux dernières conditions correspond à un bon contact thermique. Le plus souvent, il existe une différence de température proportionnelle à la composante normale de la densité de flux de chaleur, le coefficient de proportionnalité étant la résistance thermique de contact.
Méthodes de résolution
On se limitera dans ce paragraphe au cas des corps homogènes et isotropes sans sources de chaleur internes.
Régime stationnaire
Si les températures ne varient pas dans le temps, le champ de température est alors une fonction harmonique des variables d’espace x , y et z . L’équation de la chaleur s’écrit:

La détermination du champ de températures se ramène à un problème mathématique étudié depuis longtemps, pour lequel de nombreuses méthodes de résolution peuvent être appliquées: transformations conformes, analogie rhéoélectrique (cf. AÉRODYNAMIQUE, chap. 4), analogie hydrodynamique de Hele-Shaw entre l’écoulement plan des liquides parfaits et celui des liquides visqueux, etc.
Lorsque la forme du corps et les conditions aux limites sont très simples, on peut obtenir facilement des relations utiles. Soit, par exemple, une plaque ou un mur homogène d’épaisseur e dont chaque face est portée à des températures uniformes 1 et 2 mais différentes l’une de l’autre. L’intégration de l’équation (7) montre que la température à l’intérieur du mur est une fonction linéaire de la distance x à l’une des parois:
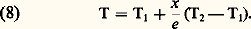
La densité de flux de chaleur qui traverse le mur est uniforme et égale à:

Il y a une analogie avec la loi d’Ohm, 﨏 étant l’analogue de l’intensité électrique, T du potentiel et/e de la conductance électrique. On désigne donc ce rapport sous le nom de conductance thermique du mur.
Soit à présent un mur constitué de n couches en matériaux différents. La loi (9) reste valable à condition de remplacer/e par l’expression:
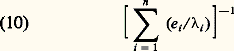
si les couches constituant le mur sont en bon contact thermique. Sinon, il faut remplacer/e par:

où Ri ,i +1 est la résistance thermique entre la couche d’indice i et la couche d’indice (i + 1). Une autre forme de corps rencontrée couramment en thermique est l’enveloppe cylindrique, par exemple en isolation. Si les températures imposées sur la surface intérieure de rayon r 1 et sur la surface extérieure de rayon r 2 sont uniformes, la température à l’intérieur de l’enveloppe est une fonction logarithmique de la distance r à l’axe du tube cylindrique:

Le flux de chaleur qui traverse l’enveloppe de longueur l sera donc égal à:

Régimes instationnaires
L’équation de la chaleur (6) est une équation aux dérivées partielles linéaires du type parabolique. On pourra ainsi obtenir la solution générale d’un problème thermique en superposant linéairement des solutions particulières.
Des solutions analytiques ont été obtenues lorsque la température ne dépend que d’une seule variable d’espace, soit d’une façon rigoureuse (problème du mur ), soit d’une façon approchée (problème de la barre ).
Soit un mur d’épaisseur e ; on peut écrire à nouveau l’équation (6) pour un champ de températures unidimensionnel:

qui devient, avec des variables sans dimensions:

où l’on a:

t étant un temps sans dimension, appelé nombre de Fourier .
L’équation (15) montre que, pour un mur d’épaisseur double par exemple soumis aux mêmes conditions thermiques sur les deux faces, le champ de températures mettra quatre fois plus de temps pour y pénétrer. La chaleur ne se propage donc pas à une vitesse constante, comme le son ou la lumière.
La solution générale de l’équation (15) s’écrit sous la forme de séries trigonométriques pour la variable sans dimensions x :
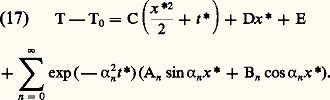
La suite 見n est la suite ordonnée de façon croissante des racines d’une équation transcendante; An , Bn , C, D et E sont des constantes.
Lorsque le nombre de Fourier est faible devant l’unité, les séries sont très faiblement convergentes. Mais on peut montrer que le champ de températures est alors de la forme:

Tout se passe comme si le milieu était semi-infini, car la température ne commence à varier qu’au voisinage de la paroi.
Lorsqu’on met en bon contact thermique deux corps A et B possédant chacun une face plane et dont les températures initiales 0A et 0B sont uniformes mais différentes, l’interface prend instantanément, en principe, une température int, intermédiaire entre 0A et 0B, qui est donnée par la formule:

La grandeur e = ‘ 連cp 福 est appelée coefficient d’arrachement de la chaleur ou effusivité thermique . Le coefficient est la conductivité thermique, 福 est la masse volumique et cp est la chaleur massique à pression constante. On comprend ainsi pourquoi du métal paraît plus froid au toucher que du bois bien qu’étant à la même température: la température de l’interface est plus faible, car l’effusivité thermique du métal est plus élevée que celle du bois.
La mesure de la température que prend l’interface permet, connaissant l’effusivité de l’un des deux corps (méthode du touchau ), de déterminer l’effusivité inconnue de l’un à l’autre. Si l’on connaît, d’autre part, la diffusivité thermique a =/ 福cp grâce à une méthode instationnaire, on déterminera ainsi la conductivité thermique sans avoir à effectuer des expériences en régime permanent, ce qui nécessite la mesure des flux de chaleur et demande parfois un temps trop important pour atteindre le régime permanent.
Lorsque le nombre de Fourier est grand devant l’unité, le premier terme de la série de (17) devient beaucoup plus élevé que les termes suivants. La distribution de température est la somme de la distribution en régime permanent (champ linéaire si 1 et 2 sont constants) et d’une expression qui décroît exponentiellement avec le temps. C’est le régime dit de Fourier qui est utilisé, en portant l’évolution des températures sur un diagramme semi-logarithmique, pour déterminer la diffusivité thermique.
Si la température imposée sur la surface d’un milieu semi-infini est périodique, de pulsation 諸, on obtient:

L’amplitude de la partie sinusoïdale de la température varie exponentiellement avec la profondeur. Elle diminue d’autant plus vite que la fréquence 諸/2 神 est plus élevée. Les variations journalières de la température dans un sol, par exemple, diminuent plus rapidement que les variations saisonnières lorsqu’on s’éloigne de la surface.
Il y a une autre configuration géométrique pour laquelle le champ de températures peut être considéré comme approximativement unidimensionnel; c’est celui d’une barre dont les extrémités sont soumises à des températures différentes. La température moyenne dans une section droite étant T, l’équation de conservation de l’énergie conduit à l’équation approchée suivante:
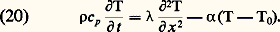
Le terme 見(T 漣 0) correspond à la dissipation de chaleur par convection entre la barre et l’atmosphère de température 0.
Changement de phase: problème de Stefan
Si la température d’un corps solide dépasse localement la température de fusion Tf , les caractéristiques thermiques sont modifiées. Il y a alors deux régions, l’une solide (indice S) où l’équation de la chaleur s’écrit:
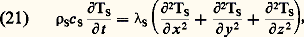
et l’autre liquide (indice L) où l’on a:
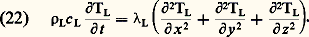
Le long du front de changement de phase, les températures sont égales à la température de fusion:

et l’on a, pour les composantes normales des densités de flux de chaleur, la relation:
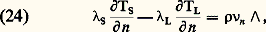
où 廬 est la chaleur latente de fusion et 益 n la vitesse normale du front.
Dans le cas d’un milieu liquide semi-infini à température uniforme Ti , sur la frontière duquel on impose brutalement à l’origine des temps une température constante 0 麗 Tf , l’abscisse du front xf est proportionnelle à la racine carrée du temps:

où 塚 est la solution d’une équation transcendante dans laquelle interviennent les caractéristiques thermiques des deux milieux et la chaleur latente de fusion. Le front de congélation avance donc à une vitesse décroissante.
3. La convection naturelle
La convection naturelle (ou libre) est le transport de chaleur dû à des mouvements de fluide provoqués par un champ de pesanteur (ou de force centrifuge). On distingue entre convection naturelle interne, qui a lieu dans une enceinte fermée à paroi non isotherme, et convection naturelle externe, qui se produit au voisinage des parois d’un corps dont la température est différente de celle de l’ambiance.
La convection interne prend naissance lorsque des perturbations du champ de températures correspondant à un régime de conduction pure croissent au lieu de s’amortir. Cela se produit pour une certaine valeur critique d’un nombre sans dimensions, le nombre de Rayleigh :
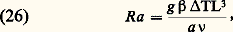
où g est l’accélération de la pesanteur, 廓 le coefficient de dilatation volumique du fluide, T une différence caractéristique de température de la paroi de l’enceinte, L une dimension caractéristique et 益 = 猪/ 福 la viscosité cinématique du fluide, 猪 étant la viscosité dynamique. Par exemple, pour l’espace compris entre deux plaques horizontales isothermes, si la plaque inférieure est la plus chaude, le nombre de Rayleigh critique est égal à 1 708.
Lorsque le nombre de Rayleigh est supérieur à sa valeur critique, le flux de chaleur qui traverse l’enceinte est supérieur à celui qu’on aurait eu par conduction seule, et le rapport des deux flux croît en fonction du nombre de Rayleigh. Cette augmentation de flux est due à la présence de tourbillons en rouleaux ou polyédriques (tourbillons de Bénard ).
La convection externe se produit au voisinage d’un objet à température différente de l’ambiance. Le champ de températures provoqué par la conduction entraîne une poussée d’Archimède qui met en mouvement vers le haut les parties les plus chaudes du fluide. En régime permanent, le transfert de chaleur s’effectue donc à la fois par conduction et par transport d’enthalpie.
Le flux de chaleur à partir du corps chauffé (ou refroidi) est sous la dépendance de deux nombres sans dimensions, le nombre de Grashof :

où L est une dimension caractéristique du corps, et le nombre de Prandtl :

Lorsque le nombre de Prandtl est assez grand (dans les huiles), le flux de chaleur ne dépend que du produit Gr 練 Pr = Ra , et, lorsque le nombre de Prandtl est assez petit (dans les métaux liquides), le flux ne dépend que du produit Gr 練 Pr 2.
Si le nombre de Grashof est suffisamment important, les variations les plus grandes de température et de vitesse ont lieu dans une zone située au voisinage immédiat du corps, qui constitue une couche limite de convection naturelle. Cette couche limite, orientée vers le haut (ou vers le bas) si le corps est chauffé (ou refroidi), peut être laminaire ou turbulente.
4. La convection forcée
La convection forcée est un transport de chaleur effectué à la fois par conduction et par transport d’enthalpie dû à la présence d’un écoulement autour de l’obstacle (plaque plane, cylindre, sphère, etc.) qui est à une température, pas forcément uniforme, différente de celle de l’écoulement. Les équations qui régissent le phénomène sont l’équation de conservation de la masse, les équations de Navier-Stokes pour la conservation de la quantité de mouvement et l’équation de conservation de l’énergie (cf. mécanique des FLUIDES). Dans la plupart des cas, l’hypothèse de la couche limite peut être faite non seulement pour le champ de vitesses (couche limite dynamique), mais encore pour le champ de températures (couche limite thermique), c’est-à-dire que l’on néglige dans les équations la composante transversale de la vitesse (perpendiculaire à l’obstacle) devant la composante longitudinale (parallèle à la surface de l’obstacle) ainsi que les dérivées longitudinales devant les dérivées transversales. Si le fluide peut être considéré comme incompressible, la connaissance des profils de vitesse suffit donc à déterminer les profils de température dans la couche limite thermique.
Couche limite incompressible
Couche limite laminaire
Les équations de la couche limite laminaire ont pu être résolues, soit d’une façon rigoureuse, soit de façon plus ou moins approchée, pour la couche tridimensionnelle sur des corps de forme quelconque à température non uniforme.
Si la température pariétale fait partie d’une famille additive de fonctions, la densité de flux de chaleur pariétale 﨏p est proportionnelle à la différence entre la température pariétale Tp et une température dite température effective eff, qui est attachée à la famille. On forme avec la densité de flux de chaleur un nombre sans dimensions, le nombre de Nusselt :
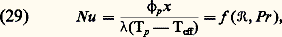
倫 étant le nombre de Reynolds (cf. mécanique des FLUIDES).
Le nom de température effective se justifie par le fait que la densité de flux de chaleur s’annule localement lorsque la distribution de température pariétale faisant toujours partie de la famille prend, au point considéré, une valeur égale à la température effective. Tout se passe comme si l’écoulement avait réellement cette température.
Lorsque le nombre de Prandtl est faible (métaux liquides), le nombre de Nusselt est fonction du produit du nombre de Reynolds et du nombre de Prandtl, appelé nombre de Péclet :
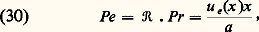
ue (x ) étant la distribution de vitesse extérieure à la couche limite.
Lorsque le nombre de Prandtl est élevé (cas des huiles), le nombre de Nusselt est le produit d’une fonction du nombre de Reynolds par la racine cubique du nombre de Prandtl.
Si la densité de flux de chaleur est nulle partout, la température pariétale est appelée température de frottement F. On définit, à partir de cette température et de la température Te à l’extérieur de la couche limite, une expression sans dimensions, le facteur thermique pariétal de frottement r . C’est une fonction croissante du nombre de Prandtl, indépendante de la distribution de vitesse extérieure ue (x ):
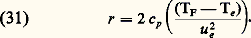
Lorsque le nombre de Prandtl est voisin de l’unité (cas des gaz), r est égal à la racine carrée du nombre de Prandtl.
Pour Pr très petit, on a l’expression asymptotique r = 0,924 練 Pr 1/2, et, pour Pr très grand, on a r = 1,922 練 Pr 1/3.
Couche limite turbulente
Dans le cas de la couche limite turbulente, les relations entre les nombres de Nusselt, de Reynolds et de Prandtl doivent être obtenues par l’expérience.
Le facteur thermique pariétal de frottement est égal à la racine cubique du nombre de Prandtl.
Couche limite à propriétés physiques variables
Pour les grandes différences de températures et les valeurs élevées du nombre de Mach Ma (cf. AÉRODYNAMIQUE, chap. 1) de l’écoulement (compressibilité), il y aura interaction entre la couche limite thermique et la couche limite dynamique. Le nombre de Nusselt est fonction non seulement du nombre de Reynolds et du nombre de Prandtl, mais encore du nombre de Mach et du nombre d’Eckert Ec:
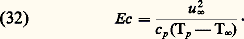
Dans la pratique, on peut étendre la validité des formules soit rigoureuses (régime laminaire), soit empiriques (régime turbulent) donnant le flux de chaleur pour un fluide incompressible, en supposant que le flux de chaleur, dans le cas de l’interaction entre le champ de températures et le champ de vitesses, sera le même que pour un fluide fictif ayant les mêmes propriétés physiques que le fluide réel à une température de référence, fonction du nombre de Mach et de la différence de températures entre l’obstacle et l’écoulement.
Soufflage ou aspiration
Lorsqu’on opère un soufflage à la paroi d’un corps, par exemple à travers une plaque poreuse, et si la température pariétale est maintenue, la densité de flux de chaleur diminue considérablement, même pour un flux massique de soufflage peu élevé. L’aspiration, au contraire, provoque une augmentation du flux de chaleur.
Convection mixte
Les deux phénomènes de convection naturelle et de convection forcée peuvent se produire lorsque la vitesse de l’écoulement est assez faible pour que les forces d’Archimède soient du même ordre de grandeur que les tensions d’origine visqueuse.
Le nombre de Nusselt est alors fonction des nombres de Grashof, de Reynolds et de Prandtl.
5. Applications
Les applications thermiques couvrent le champ presque entier des activités industrielles (production d’énergie, sidérurgie, mécanique, électronique, génie chimique, bâtiment, alimentation), des plus traditionnelles aux plus modernes. Elles s’étendent à l’agriculture, à l’élevage, à la biologie et à la médecine. Les vestiges de l’Antiquité portent le témoignage des réalisations pratiques où production, accumulation et transfert de chaleur sont déjà mis en œuvre pour cuire les aliments, chauffer les habitations et transformer la matière (outils et armes).
Foyers et chauffages
Foyers domestiques
Dans les foyers, la chaleur s’utilise directement par conduction («feu» de cuisson) et par rayonnement (four), la cuisson au sein d’un liquide (eau bouillante) faisant intervenir dans le contenant des phénomènes de convection.
Chauffage domestique
Le chauffage domestique se fait par répartition de sources de chaleur isolées (cheminées, poêles et radiateurs) ou par distribution de chaleur à partir d’une source unique (chaufferie du chauffage central). Si les sources localisées sont visibles (feu, flamme de brûleur, incandescence des résistances électriques), le rayonnement prédomine; si les sources sont enfermées dans une enceinte, le rayonnement reste important avec les grandes surfaces extérieures (poêle en faïence), mais, avec des appareils de plus faibles dimensions, la convection naturelle (poêle en fonte, radiateur à circulation d’huile ou à catalyse) et la convection forcée (radiateur soufflant) prédominent sur le rayonnement. Avec le chauffage central, la distribution de chaleur s’effectue à l’aide d’un fluide caloporteur circulant dans des gaines (air) ou des tuyauteries (eau, vapeur d’eau) par effet de thermosiphon (circulation naturelle par différences de densités) ou par un moyen mécanique (respectivement: ventilateur ou pompe). Dans un cas, l’air chaud est distribué directement dans les pièces, dans l’autre, le fluide caloporteur fournit la chaleur par convection à des éléments tubulaires en fonte ou en tôle qui constituent les surfaces chauffantes statiques (radiateurs ou convecteurs) de chaque pièce. Les radiateurs cèdent la chaleur par convection naturelle, les convecteurs, nichés dans les murs et munis d’ailettes, cèdent cette chaleur par convection forcée. La distribution peut s’effectuer par panneaux rayonnants (tuyauteries noyées dans les murs, le plafond ou le sol). Le chauffage par le plafond est activé par convection, à l’aide d’un ventilateur assurant une circulation d’air.
Chauffages collectifs
Le mode de chauffage collectif diffère selon les dimensions et l’occupation, permanente ou temporaire, des locaux. Le chauffage central fait appel à des batteries de chaudières (îlots d’habitations) ou au chauffage urbain (quartiers ou villes). Des pompes assurent la circulation du fluide caloporteur (eau surchauffée ou vapeur d’eau), les canalisations étant calorifugées, ce qui réduit les déperditions entre la centrale thermique et le quartier de la ville. Le chauffage à air chaud pulsé (aérothermes) convient pour un usage intermittent (ateliers); les panneaux rayonnants s’adaptent aux locaux de grandes dimensions à condition d’organiser une circulation d’air évitant l’accumulation de chaleur dans les parties hautes inoccupées. Les rampes à rayonnement infrarouge s’installent dans les espaces aérés (marchés, halls de gares) ou dans de vastes édifices (églises). L’énergie géothermique sert au chauffage de Reykjavik (Islande), l’eau chaude (de 87 à 110 0C) arrivant par pipe-lines de 30 kilomètres de distance. L’énergie solaire est utilisée au chauffage de l’eau par accumulation, au Japon par exemple.
Échangeurs de chaleur et dispositifs de transfert thermique
Principe des échangeurs
La récupération de l’énergie calorifique en fin d’opération industrielle (chaleur sensible des fumées, des produits sortant des fours, des vapeurs ou gaz sortant des turbines) est assurée par des échangeurs. Le refroidissement et le chauffage nécessaires au bon fonctionnement de divers appareils et installations sont réalisés à l’aide d’échangeurs ou de systèmes de transfert thermique.
Dans un échangeur, la chaleur est transmise d’un fluide à un autre. Le même fluide peut conserver son état physique (liquide ou gazeux) ou se présenter successivement sous les deux phases (cas des condenseurs et des vaporiseurs).
Le type le plus simple comprend un récipient (ou canalisation) dans lequel les deux fluides sont directement mélangés et atteignent la même température finale. Les réchauffeurs d’eau (injection de vapeur d’eau sous pression), les désurchauffeurs industriels et les condenseurs à injection (centrales thermiques) sont des exemples de tels appareils appelés échangeurs à contact direct .
En principe, pour les échangeurs les plus répandus dans l’industrie, les deux fluides, désignés par 1 et 2, s’écoulent dans des espaces séparés par une paroi, ou cloison, à faible inertie thermique. La chaleur que le fluide 1 cède à la paroi, par convection le long de la surface de contact, traverse l’épaisseur de la paroi par conduction et est cédée au fluide 2 par convection le long de l’autre face.
Les processus de transfert présentent une réciprocité: convection (1), conduction (paroi), convection (2). Le flux de chaleur échangé, en W 練 m size=1漣2, s’exprime par le produit d’une conductance globale, en W 練 m size=1漣2 練 0C size=1漣1, constante ou non le long de l’échangeur, et de la différence T entre les températures moyennes 1 et 2 des fluides (fig. 2, 3 et 4).
Il existe trois types d’échangeurs selon le mode respectif des écoulements des deux fluides. Les figures 2, 3 et 4 représentent des éléments très simplifiés de chacun d’entre eux. Dans les deux premiers types, les deux écoulements ont des directions parallèles mais des sens identiques dans le premier (co-courant ) et des sens opposés dans le second (contre-courant ). L’avantage de l’échangeur à contre-courant sur l’échangeur à co-courants est de nécessiter, pour un même flux de chaleur, des surfaces plus faibles. L’échangeur à courants croisés présente trois dispositions différentes selon que les fluides 1 et 2 sont respectivement brassés ou non. Dans le cas de la figure 4, le fluide 1 est canalisé et par suite non brassé, le fluide 2 s’écoule librement entre les plaques et peut être considéré comme partiellement brassé du fait de tourbillons générés par les tubes. D’autres configurations d’échangeurs à courants croisés sont utilisées, par exemple les échangeurs dits platulaires , dans lesquels les deux fluides passent entre de multiples plaques jointives (fig. 5); de tels échangeurs peuvent être d’une fabrication très économique. Lorsqu’un fluide change de phase, que ce soit dans un condenseur (fig. 6) ou dans un vaporiseur, le coefficient d’échange est considérablement accru compte tenu de la chaleur de changement d’état, le bon rendement de l’échangeur étant maintenu par une augmentation des surfaces (ailettes) du côté du fluide convectif (aérocondenseur). Ces trois types d’échangeurs sont appelés récupérateurs ; ils servent à chauffer, à refroidir, à évaporer ou à condenser toutes sortes de fluides.
Classification des échangeurs
La construction des échangeurs introduit deux grandes catégories: les échangeurs tubulaires à corps cylindriques et les échangeurs compacts dans lesquels coexistent fréquemment les trois modes d’écoulement relatif des fluides.
Les échangeurs tubulaires comprennent un distributeur, un corps de calandre et une boîte de retour ou fond de calandre. Les surfaces d’échange peuvent atteindre plusieurs milliers de mètres carrés, les faisceaux tubulaires prenant des formes très diverses: faisceaux en épingle à cheveux (réchauffeur d’air, corps de chauffe des bouilleurs), faisceaux constitués de tubes enroulés couche par couche, alternativement à droite et à gauche autour d’un axe central présentant une grande surface (10 000 m2) avec des écarts de températures des fluides de 2 à 3 0C (échangeurs bobinés utilisés dans l’industrie frigorifique). Il faut cependant ajouter qu’il est plus avantageux de multiplier le nombre de circuits indépendants que celui des passages d’un même circuit, car, au-delà du cinquième, ils sont totalement inefficaces.
Les échangeurs compacts sont construits pour présenter le maximum de surface dans un volume donné (jusqu’à 1 000 mètres carrés par mètre cube): ils comprennent des tubes ailetés ou des éléments en tôle tels que des plaques planes ou ondulées, des plateaux, des lames plates ou spiralées. La qualité essentielle d’un tube à ailettes réside dans la bonne liaison thermique entre la surface secondaire (ailette) et le tube (refroidisseurs d’air de compresseurs terrestres). Les échangeurs en tôles planes empilées et séparées par des ondulations, ou épingles, conviennent aux gaz à basse pression et aux liquides mauvais conducteurs, les ondulations jouant le rôle d’ailettes. Ces échangeurs compacts entrent dans la conception des appareils de production de gaz (éthylène), de liquéfaction (gaz naturel, hydrogène, hélium). Ces échangeurs à plateaux, facilement démontables pour le nettoyage, servent dans l’industrie alimentaire (pasteurisation des jus de fruits, refroidissement du lait frais) et dans le traitement des matières plastiques.
Grâce à leur grande compacité (possibilité de miniaturisation), les échangeurs trouvent de multiples applications en électronique, en aéronautique et en astronautique. Les échangeurs en graphite présentent l’avantage d’une bonne conductivité, de l’anticorrosion (fabrication d’acides et dérivés), de la non-contamination (préparation des médicaments et des aliments en conserve et en jus) sur les échangeurs les plus courants. Un autre dispositif de transfert de chaleur entre deux fluides est le régénérateur à fonctionnement cyclique (le plus connu porte le nom de Cowper, qui l’a appliqué au haut fourneau). Cet appareil de très grandes dimensions (sous forme de tour) comprend un seul passage rempli d’un empilage fixe (briques réfractaires ou mullite), appelé le ruchage, qui joue alternativement le rôle de puits et de source de chaleur. Dans une phase du cycle, le fluide 1, constitué par les fumées du foyer industriel, traverse le passage unique et cède sa chaleur par convection au ruchage; dans l’autre phase, le fluide 2, c’est-à-dire l’air destiné à la combustion ou «vent» de haut fourneau et éventuellement le combustible gazeux, récupère cette chaleur par le même processus de convection. La configuration de ces régénérateurs correspond à celle des échangeurs à contre-courant. Le schéma du cycle thermique est le suivant: dans la phase 1, convection (fluide 1), conduction et accumulation (ruchage); dans la phase 2, convection (fluide 1), conduction et déperdition (ruchage). En général, le fonctionnement s’effectue en couplage; à la phase 1 dans l’un des appareils correspond simultanément la phase 2 dans l’autre.
Un système mécanique provoque périodiquement l’inversion dans le circuit des fluides. L’avantage de ces appareils est de fournir un préchauffage très uniforme de l’air destiné aux foyers industriels et à un niveau de température élevé (1 700 K pour les cowpers); l’inconvénient provient des difficultés d’inverser les circuits des fluides et d’assurer une parfaite étanchéité dans les organes de cette inversion. Ces régénérateurs s’appliquent au four Martin, au four à cuve de verrerie, au four à coke, au haut fourneau et quelquefois à l’industrie chimique, mais la tendance actuelle est de les remplacer par des récupérateurs, principalement dans les fours poussants (cf. MÉTALLURGIE - Les fours métallurgiques, chap. 2).
Les régénérateurs rotatifs des installations de turbines à gaz comportent une colonne compacte de remplissage, de dimensions réduites, tournant dans un cylindre. Celui-ci est séparé suivant l’axe en deux compartiments étanches dans lesquels circulent le fluide 1 (gaz d’échappement), d’une part, et le fluide 2 (air destiné à la combustion), d’autre part. Dans le mouvement de rotation, la colonne de remplissage passe régulièrement du rôle d’accumulateur au rôle de déperditeur de chaleur.
Échangeurs particuliers
Un autre type d’échangeur comporte également une colonne fixe de remplissage; c’est celui où les deux fluides coexistent dans le passage en circulant à contre-courant, le garnissage permettant le contact direct entre les deux fluides.
Les tours de refroidissement sont un exemple courant de ce type: elles permettent de réemployer l’eau utilisée dans divers échangeurs d’une centrale thermique. Cette eau chaude, pompée au sommet de la tour, descend par gravité en s’étalant sur les surfaces du garnissage et reste ainsi en contact continu avec l’air. L’air s’humidifie et, dans ce cas, le transfert de chaleur est donc accompagné d’un transfert de masse. Les refroidisseurs à grilles avec déchargement de matière granulaire assimilable à un fluide homogène peuvent être considérés comme des échangeurs à courants croisés.
Les systèmes à lits fluidisés , constitués par une matière finement divisée, sont rattachés aux échangeurs à cause de l’aspect fluide que prend la poudre en suspension: celle-ci reçoit de la chaleur d’une source extérieure et la transmet avec un très grand coefficient d’échange au fluide qui traverse le lit en le fluidisant (cracking catalytique du pétrole à la pression atmosphérique).
Procédés de refroidissement
La dissipation de la chaleur provenant d’une source peut se réaliser directement par conduction à travers les structures jusqu’aux surfaces extérieures, qui sont refroidies par convection naturelle de l’air ambiant et par rayonnement (cf. tableau). La présence d’un fluide intermédiaire qui baigne les parois directement chauffées par une source très localisée contribue à uniformiser la température dans les structures conduisant la chaleur vers l’extérieur.
Cette dissipation de la chaleur provenant d’une source peut être facilitée par l’utilisation des changements d’état du fluide caloporteur: cela conduit à la réalisation de dispositifs appelés caloducs (fig. 7), qui ont la commodité de pouvoir se présenter sous forme de conduites souples et de remplacer tout organe moteur par les forces de capillarité. La difficulté de cette technique réside dans le choix et la mise en circulation du fluide caloporteur.
Le transfert de chaleur entre source et puits à des niveaux de températures extrêmes nécessite des fluides spéciaux, gaz liquéfiés pour basse température ou métaux liquides pour températures élevées, agissant en circuit fermé et étanche. Citons les exemples du refroidissement des supraconducteurs par l’hélium liquide [cf. SUPRACONDUCTIVITÉ] et de celui des réacteurs nucléaires par le sodium (cf. industrie NUCLÉAIRE - Réacteurs nucléaires). Le refroidissement des parois chauffées par des gaz chauds (combustion) ou des gaz à grande vitesse (échauffement cinétique) s’effectue du côté non exposé de la paroi soit par circulation d’un réfrigérant qui, dans le cas d’une combustion, est un mélange du combustible et du comburant, soit par injection d’un liquide ou d’un gaz à travers une paroi percée de trous ou de fentes (protection par film) ou à travers une paroi poreuse (suage). En régime transitoire, le fonctionnement étant alors d’une durée limitée, la paroi possède un revêtement consommable (réaction endothermique dans la couche en fusion ou en évaporation). Cette protection par ablation est utilisée sur le bouclier thermique des capsules de rentrée des astronautes et dans les tuyères de fusée.
Le rayonnement thermique constitue un mode simple et efficace de refroidissement pour des surfaces portées à haute température ou des surfaces internes qui possèdent un grand angle d’ouverture vers l’atmosphère (tuyère ouverte).
Un autre mode simple de refroidissement sans organe moteur consiste à utiliser la convection naturelle. C’est un procédé de ce genre qui intervient dans le transport, par exemple pour leur retraitement, de matériaux radioactifs dont la puissance résiduelle est encore notable. Le «château de transport» utilisé renferme une «grappe» d’une centaine d’éléments combustibles tels que celui de la figure 8, qui baignent dans un fluide caloporteur assurant une répartition uniforme des températures grâce à une convection naturelle qui peut présenter plusieurs régimes (pseudoconvection, thermosiphon fermé).
Isolation thermique
Les surfaces externes d’un système thermique échangent de la chaleur avec l’environnement; l’isolation thermique consiste à munir ces surfaces d’un revêtement statique mauvais conducteur de la chaleur. Il se crée alors entre les deux faces de l’isolant un fort gradient de température dont le sens est fixé par celui de l’écoulement de la fuite. Il en résulte, en particulier, une diminution de température de la nouvelle surface externe de l’installation, dans le cas d’une source, et une augmentation de cette même température, dans le cas d’un puits. L’écart de température T (cf. tableau) se trouve diminué, ce qui a pour effet de réduire la fuite thermique. L’isolation thermique peut être recherchée pour la protection contre les excès de températures très élevées ou très basses. L’isolation thermique peut être permanente (fils et câbles d’une installation électrique, fours et armoires frigorifiques) ou temporaire (vêtements de pompiers, gants de manutention, boîtes de transport de glaces et sorbets).
Les isolants sont appelés calorifuges. Il existe quatre grandes catégories d’isolants, selon la répartition de la matière: granulaire (sable), fibreuse (laine de verre, d’amiante, de graphite) ou cellulaire (résines synthétiques expansées, plâtres), ou bien selon la structure en fines feuilles réfléchissantes (alfol). Les qualités d’isolation pour les trois premières catégories sont dues à leur porosité (fibres superfines, poudres, résines expansées); elles peuvent atteindre l’isolation de l’air lorsque les pores sont fermés. Les progrès considérables dans la fabrication de matériaux isolants ont transformé profondément toutes les techniques de l’habillement, de l’habitat, de la construction et des moyens de transport.
Transmission de chaleur dans les fours industriels
La conception d’un four dépend des processus de transfert de chaleur qui se développent dans les différentes zones entre la charge , subissant des transformations physiques ou chimiques ou un formage, et la source , constituée par les produits de la combustion, l’électricité ou l’énergie solaire. Dans un four à combustion, par exemple, la chaleur se répartit selon le schéma suivant: les produits de la combustion fournissent les flux de chaleur Qc et Qp , respectivement à la charge et à la paroi, par rayonnement et par convection. Une partie de Qp , par suite du contact de la charge avec la paroi, est restituée à la charge par rayonnement et par conduction. Celle-ci peut éventuellement fournir de la chaleur aux fumées et à la paroi au cours d’une réaction exothermique, dans la zone de «clinkérisation» dans le four à ciment, par exemple. Une grande partie de la chaleur sensible des fumées et de la matière est récupérable, à leur sortie du four, dans des récupérateurs, des régénérateurs ou des refroidisseurs à grilles. Les pertes inévitables s’effectuent vers l’extérieur par les ouvertures et les parois. Le bilan thermique global du four est alors établi à partir des bilans de chacune des zones où la quantité de chaleur doit être fournie à un niveau de température rigoureusement déterminé par la réaction physique ou chimique qui s’y produit.
Applications diverses
Les procédés de transfert de chaleur sont utilisés dans les diverses branches de la médecine, par exemple pour des installations de service (couveuse), pour des traitements par hypothermie, pour la conservation de médicaments et de plasma sanguin, pour la stérilisation des pansements et des instruments chirurgicaux, etc.; l’élevage des animaux fait intervenir des installations thermiques analogues (couveuses artificielles). En agriculture, l’effet de serre est développé industriellement pour fournir toute l’année fleurs, fruits et légumes frais. La quasi-totalité de l’énergie solaire (émise entre 0,25 et 3 猪m du spectre) traverse les parois de verre ou de certaines matières plastiques et se trouve piégée dans la serre, car ces parois restent opaques au rayonnement terrestre émis, à température plus basse, dans le domaine des grandes longueurs d’onde. La protection, contre le rayonnement du ciel froid, des vignes et des orangers est réalisée par un écran de fumée, produit de la combustion du mazout ou de feuilles mortes et déchets; par la même occasion, l’air environnant se trouve chauffé. L’extraction du sel d’eau de mer s’effectue, selon les régions, par évaporation dans les marais salants (source naturelle de chaleur solaire) ou par congélation (puits de chaleur des pays septentrionaux). Dans l’industrie alimentaire, la chaleur solaire a permis de tout temps la conservation des fruits et légumes par dessiccation ainsi que le séchage des graines; ces opérations sont actuellement perfectionnées avec des sources de chaleur électrique et des techniques nouvelles telle la lyophilisation.
thermique [ tɛrmik ] adj.
1 ♦ Phys. Relatif à la forme d'énergie appelée chaleur, qui se traduit par des sensations spécifiques chez l'homme (⇒ chaud, 2. froid), par des phénomènes physiques, et à laquelle correspond la température. Effet thermique : échange d'énergie thermique par conduction, convection ou rayonnement. ⇒ calorifique. Interaction thermique entre un système et un thermostat. Équilibre thermique. Conductibilité thermique. — Science thermique ou n. f. la thermique. ⇒ thermodynamique.
♢ Techn. Isolation thermique. Barrière thermique, bouclier thermique. Captation thermique. Analyse thermique : enregistrement continu des variations de température d'un système, en fonction du temps.
2 ♦ Cour. Moteur thermique, qui transforme l'énergie thermique en énergie mécanique (machine à vapeur, moteur à explosion, à réaction). Propulsion thermique. ⇒ thermopropulsion. Voiture thermique (opposé à électrique). Centrale thermique, utilisant des moteurs thermiques pour produire l'énergie électrique. Pollution thermique, résultant de la décharge d'air ou de liquide chauffés dans les lacs ou les rivières, à l'origine d'une élévation de la température de l'eau et du déséquilibre de la balance écologique. — Inform. Imprimante thermique, utilisant un papier thermosensible. — Métrol. (appareils de mesure) Dont l'indication est liée à une dissipation de chaleur. Voltmètre thermique. — Biol. Choc thermique : brusque élévation de température. — Adv. THERMIQUEMENT .
● thermique adjectif Relatif à la chaleur, à la température. Électricité Se dit d'un appareil de mesure dont l'indication est commandée par la variation de température due au passage d'un courant. Militaire Se dit du rayonnement infrarouge émis par un corps chaud (moteur notamment) et d'une lunette permettant de le détecter. ● thermique (expressions) adjectif Analyse thermique, étude du refroidissement ou de l'échauffement des substances, mettant en évidence leurs modifications chimiques. Papier thermique, papier couché, utilisé notamment pour la télécopie, et portant sur une face un réactif qui devient bleu ou noir sous l'effet de la chaleur (entre 90 et 110 °C). Centrale thermique, centrale dans laquelle l'énergie électrique est produite à partir d'énergie thermique. Signature thermique, ensemble des points lumineux émis par un char en fonction de son rayonnement thermique et permettant de l'identifier. Sensibilité thermique, domaine de la sensibilité qui concerne la perception de variations de température du revêtement cutané et de l'intérieur du corps. Neutron thermique, neutron en équilibre thermique avec les atomes du milieu où il se trouve. (À la température ordinaire, l'énergie des neutrons thermiques est voisine de 0,025 eV.) Réacteur thermique, réacteur nucléaire dans lequel la plupart des fissions sont provoquées par des neutrons thermiques. Équilibre thermique, situation dans laquelle des corps en contact thermique n'échangent pas de chaleur. Machine thermique, machine servant à convertir de la chaleur en travail (moteur) ou à transférer de la chaleur d'une source à une certaine température à une autre source à une autre température en utilisant un moteur (machine frigorifique, pompe à chaleur). ● thermique nom masculin Courant vertical déclenché par la thermoconvection. ● thermique nom féminin Partie de la physique et de la technique qui traite de la production, de la transmission et de l'utilisation de la chaleur.
thermique
adj. et n. f.
d1./d adj. Qui a rapport à la chaleur, à l'énergie calorifique.
— Machine thermique, qui transforme l'énergie calorifique en une autre forme d'énergie. Centrale thermique, dans laquelle l'électricité est produite à partir de la chaleur de combustion du charbon, du gaz ou du pétrole.
d2./d n. f. PHYS étude de la chaleur et des phénomènes calorifiques (thermométrie, calorimétrie, étude des combustions, etc.).
⇒THERMIQUE, adj. et subst. fém.
I. — Adjectif
A. — SC., PHYS. Qui se rapporte à la forme d'énergie qu'est la chaleur.
1. [En parlant de la sc. rel. à cette forme d'énergie et de ses méthodes] On retrouve là le rôle d'une élévation de température, considéré dans la théorie thermique, et dont l'intervention paraît être très fréquente dans le début des mouvements cycloniques (MAURAIN, Météor., 1950, p. 77).
♦ Les sciences thermiques. Synon. de thermique (infra II). Le deuxième sujet très important des sciences thermiques concerne les recherches sur le transfert de chaleur: conduction, convection et rayonnement, principalement (Les Sc. mécan. et l'avenir de la Fr., Paris, La Docum. fr., 1980, p. 231).
♦ Analyse thermique. ,,Mode d'étude d'une substance, en particulier d'un métal, d'un alliage, d'un corps polymorphe, en suivant sa vitesse d'échauffement ou de refroidissement en fonction de la température`` (DUVAL 1959). V. dilatométrie rem. s.v. dilatomètre ex. de Caillère et Hénin.
♦ Bilan thermique. Quantité de chaleur qui est produite ou absorbée dans une réaction chimique, entre l'état initial et l'état final. C'est donc le dégagement de la chaleur de changement d'état qui rend positif le bilan thermique de la réaction d'hydratation et rend celle-ci possible (CLÉRET DE LANGAVANT, Ciments et bétons, 1953, p. 38).
♦ Diagramme thermique. ,,Diagramme représentant l'état d'un mélange en fonction de la température`` (DUVAL 1959).
2. [En parlant de cette forme d'énergie en tant que phénomène phys., de ses effets] Phénomène, processus thermique; instabilité, rayonnement, transfert, vibrations thermique(s); échanges thermiques; déformations thermiques des matériaux. Plus un tissu contient d'air, moins il se laisse traverser par les radiations thermiques (MACAIGNE, Précis hyg., 1911, p. 174). Le spectre est très différent de celui d'une source thermique, notamment par l'intensité beaucoup plus grande du rayonnement, dans l'ultraviolet (SCHATZMAN, Astrophys., 1963, p. 126).
♦ Énergie, équilibre thermique. Agitation thermique.
♦ Choc thermique. Changement de température très rapide. Leur résistance [des verres vitro-cristallins] aux chocs thermiques n'est pas dépassée par la meilleure porcelaine, d'où la fabrication des nez de fusées et d'engins téléguidés, car ils résistent aux énormes vitesses (Cl. DUVAL, Verre, 1966, p. 85).
♦ Conduction thermique. Propagation de la chaleur, de l'électricité à travers les corps conducteurs. Coefficient de conduction thermique, p. ell. coefficient thermique. Harrison réussit le premier à éliminer les effets de la température sur le système (...) en combinant plusieurs métaux à coefficient thermique distinct (BASSERMANN-JORDAN, Montres, horl. et pend., 1964, p. 171). V. conduction ex. 1.
♦ Convection thermique. ,,Transport de chaleur par circulation automatique d'un fluide (liquide ou gaz) dû à la différence de température et de densité`` (DUVAL 1959). Convection thermique et diffusion chimique peuvent effectivement modifier l'énergie disponible (FURON ds R. gén. sc., t. 63, 1956, p. 41).
♦ Effets thermiques. Émission ou absorption d'énergie, par conduction, convection ou rayonnement. Le courant peut se manifester non seulement par des effets mécaniques, mais par des effets chimiques, thermiques, lumineux, etc. (H. POINCARÉ, Valeur sc., 1905, p. 228).
♦ Émission, rayonnement thermique. Rayonnement produit par un corps solide, liquide ou gazeux à l'état d'équilibre thermodynamique. Nous avons déjà envisagé l'absorption et l'émission thermique qui prennent place dans la couronne, pour les longueurs d'onde décimétriques et métriques qui en proviennent (SCHATZMAN, Astrophys., 1963, p. 54). Relations très générales entre matière et lumière, qui se manifestent dans le rayonnement thermique du corps noir (Hist. gén. sc., t. 3, vol. 2, 1964, p. 216).
♦ ACOUST. Bruit thermique. Bruit dont l'origine est liée à l'agitation électronique dans les matériaux conducteurs d'électricité. Le bruit thermique étant le type même de l'émission incohérente (Hist. gén. sc., t. 3, vol. 2, 1964, p. 323).
♦ CLIMATOL., MÉTÉOR., ENVIRONNEMENT. Qui est relatif à la température d'un lieu. Régime thermique; état thermique de l'intérieur de la terre; contraste thermique entre l'été et l'hiver; stabilité, instabilité thermique; ascendance thermique. On a pu néanmoins les grouper [les climats] d'après la latitude en un certain nombre de grands types généraux constituant à la surface de la terre des zones thermiques (PLANTEFOL, Bot. et biol. végét., t. 2, 1931, p. 527). Tandis qu'on a quelques données (...) sur la pollution thermique des eaux, on en a beaucoup moins sur la pollution thermique de l'atmosphère (Le Sauvage, 1er avr. 1977, p. 109, col. 1). Carte thermique. ,,Carte donnant la température moyenne ou les températures extrêmes des pays qui y sont représentés`` (GDEL).
Gén. au plur. Conditions thermiques. Conditions de température. Théoriquement, dans l'air ou dans le sol, la plante trouve à peu près des conditions thermiques comparables (PLANTEFOL, Bot. et biol. végét., t. 2, 1931, p. 525). Pour se soustraire à la condition thermique de l'eau de surface, il est possible d'envisager le réchauffement, par l'énergie solaire, de vastes bassins dont l'évaporation aurait été supprimée (ROMANOVSKY, Mer, source én., 1950, p. 26).
Courant thermique ou, absol., thermique, subst. masc. Courant vertical déclenché par les variations de pression atmosphérique. V. pulsatif ex. de Jeux et sports.
3. [En parlant des caractéristiques et des propriétés de cette forme d'énergie] Capacité thermique; conductance, conductivité, dilatation, puissance thermique; constance thermique; propriétés thermiques des corps. On ne saurait dans ces transferts de chaleur attribuer un rôle important à la conductibilité thermique moléculaire de l'air, qui est très faible (MAURAIN, Météor., 1950, p. 53). Ce moteur à haut rendement thermique (grâce en particulier à son taux de compression très élevé destiné à produire l'auto-allumage) brûle un combustible moins cher que l'essence (TINARD, Automob., 1951, p. 336).
♦ Diffusion thermique. Processus de diffusion produite par des gradients thermiques. Synon. thermodiffusion (s.v. thermo-). Les processus d'amortissement, plus spécialement la diffusion thermique, effacent les fluctuations (P. MANNEVILLE, Structures dissipatives, chaos et turbulence, Saclay, C.E.A., 1991, p. 50).
♦ Neutrons thermiques. Neutrons lents, en équilibre thermique avec le milieu, possédant une énergie cinétique du même ordre que celle des molécules d'un gaz à la température ordinaire. La section efficace de fusion d'un noyau d'uranium 235 vaut 550 barns [unité de surface valant 10-24 cm2] pour un neutron thermique de 0,05 eV et seulement 3 barns pour un neutron rapide de 0,3 MeV (SARM. Phys. 1978).
4. [En parlant des applications de cette forme d'énergie] Procédé thermique. Quelques types [de four] trouvent des applications dans les traitements thermiques (GUILLET, Techn. métall., 1944, p. 88). Cours de perfectionnement de maîtrise de 3 à 6 mois (...) (distribution, production thermique ou hydraulique, transport de l'électricité et équipement) (Encyclop. éduc., 1960, p. 280).
a) [En parlant d'un appareil, d'un instrument, d'une installation, d'un matériau de protection]
 ) Qui fonctionne par effet thermique, par différence de température. Ampèremètre, voltmètre thermique; siphon thermique. Réacteur thermique (Nucl. 1975).
) Qui fonctionne par effet thermique, par différence de température. Ampèremètre, voltmètre thermique; siphon thermique. Réacteur thermique (Nucl. 1975). ♦ Détecteur thermique. Appareil servant à détecter les ondes électromagnétiques, dont le principe consiste à porter à une température élevée un fil métallique de très petit diamètre. La sensibilité du « détecteur thermique » est indépendante de la longueur d'onde du rayonnement incident (PAUL Télédétection 1982).
 ) Qui produit de l'énergie par transformation de l'énergie thermique.
) Qui produit de l'énergie par transformation de l'énergie thermique. ♦ Centrale, usine thermique. Centrale, usine qui utilise des installations de conversion thermique pour produire de l'énergie électrique. D'autres usines de pompage ont été installées, notamment dans la Ruhr, en demandant l'énergie de pompage (...) à des usines thermiques (THALLER, Houille blanche, 1952, p. 34). Une centrale nucléaire est analogue à une centrale thermique car le combustible fissile y joue, sous forme beaucoup plus concentrée, le même rôle que le charbon ou le mazout (GOLDSCHMIDT, Avent. atom., 1962, p. 107).
♦ Machine, moteur thermique. Machine, moteur qui transforme l'énergie thermique en énergie mécanique. On énonce quelquefois ce principe [second principe de la thermodynamique] sous la forme suivante:Il est impossible de faire fonctionner une machine thermique avec une seule source de chaleur (H. POINCARÉ, Thermodyn., 1892, p. 120). Moteurs Diesel, comme tout moteur thermique à pistons, ne pouvant travailler que dans des limites de vitesses relativement restreintes (BAILLEUL, Matér. roulant ch. de fer, 1951, p. 87). V. cycle1 II A 1 b ex. de Poincaré.
♦ ART MILIT. Lunette thermique. ,,Lunette dotée d'un système à infrarouge thermique, qui transforme en lumière visible le rayonnement thermique des objectifs et de leur environnement`` (GDEL). Une lunette thermique équipe le poste de tir du missile Milan et permet le tir antichar de nuit et par mauvaise visibilité (GDEL).
♦ INFORMAT., REPROGR. Imprimante thermique. ,,Type d'imprimante où l'impression est assurée par une « brûlure » du papier`` (MESS. Télém. 1979).
 ) Qui sert de protection contre la chaleur. Bouclier thermique; écran thermique (d'un réacteur nucléaire); isolement, isolation thermique. La fabrication du verre mousse, isolant thermique de faible densité apparente (environ 0,15), repose sur le chauffage en moules d'acier inoxydable d'un mélange de poudre de verre et de charbon de bois (Cl. DUVAL, Verre, 1966, p. 108).
) Qui sert de protection contre la chaleur. Bouclier thermique; écran thermique (d'un réacteur nucléaire); isolement, isolation thermique. La fabrication du verre mousse, isolant thermique de faible densité apparente (environ 0,15), repose sur le chauffage en moules d'acier inoxydable d'un mélange de poudre de verre et de charbon de bois (Cl. DUVAL, Verre, 1966, p. 108). b) [En parlant d'un processus] Procédés d'extraction thermique. ,,Procédé faisant appel à la chaleur pour faciliter, par abaissement de la viscosité, l'extraction de pétroles bruts sensiblement visqueux et situés généralement à de faibles profondeurs`` (BARBIER Pétrole 1980).
B. — PHYSIOL., PATHOL., NEUROBIOL.
1. Qui se rapporte à la température du corps. Courbe, décalage, réaction, poussée thermique. Si, lors de la deuxième baisse thermique, on réchauffe l'insecte avant que la température de ses tissus ne soit tombée à -10, on réussit à le ranimer (J. ROSTAND, La Vie et ses probl., 1939, p. 104). Si l'élévation thermique est faible il faut avant de parler de fièvre s'entourer de certaines précautions (QUILLET Méd. 1965, p. 194). Abaissement thermique.
♦ Préférendum thermique. ,,Température optimale choisie par un animal de préférence à toute autre`` (PIÉRON 1973). Synon. thermopréférendum (s.v. therm(o)-).
♦ Régulation thermique. Synon. de thermorégulation. La thyroïde a également une action sur la régulation thermique. Elle stimule les contractions cardiaques et le débit sanguin (QUILLET Méd. 1965, p. 471).
2. Qui se rapporte à la température ressentie par le corps, à la sensation de chaleur.
♦ Sensation thermique. Sensation correspondant à la réaction au chaud ou au froid. Un excitant donne lieu à une sensation tactile ou à une sensation thermique (MERLEAU-PONTY, Phénoménol. perception, 1945, p. 89). Des sensations tactiles et thermiques de la langue (PIÉRON, Sensation, 1945, p. 41).
♦ Sensibilité thermique. Domaine de la sensibilité concernant la détection et la perception de variations de température au niveau du revêtement cutané et de l'intérieur du corps. Les sensibilités tactile douloureuse et thermique sont intactes (Ce que la Fr. a apporté à la méd., 1946 [1943], p. 246). Perte de la sensibilité thermique et douloureuse (QUILLET Méd. 1965, p. 350).
II. — Subst. fém. Science qui traite de la production d'énergie, en particulier de chaleur, et de leurs transferts par conduction, convection ou rayonnement, ou par le couplage de ces phénomènes. Son œuvre [de Fourier] est l'acte de naissance de cette science type de l'ingénieur qu'est la thermique (...). La thermique assure une réalité plus complexe [que la thermodynamique] en se plaçant carrément et d'emblée dans les processus des phénomènes irréversibles en introduisant ce paramètre essentiel qu'est le temps (La Rech. à l'École Centrale, 1980, p. 296). Nous n'envisagerons ici que le cas des échangeurs car il illustre typiquement l'état de la thermique en France (Les Sc. mécan. et l'avenir de la Fr.Paris, La Docum. fr., 1980, p. 234).
REM. 1. Thermicien, -ienne, adj. et subst. Spécialiste de la thermique. Société Française des Thermiciens. Selon les thermiciens mieux valait orienter d'abord les investissements vers les installations qui économisent l'énergie (CHENOT, Entr. national., 1956, p. 52). Confronté aux problèmes industriels relevant de la thermique, le thermicien se doit d'être simultanément: spécialiste de méthodes numériques, mécanicien des fluides, spécialiste de l'interaction matière rayonnement (La Rech. à l'École Centrale, 1980, p. 298). En appos. Deux étudiants (...) pourraient, à ce moment, diverger pour devenir:— le premier, ingénieur thermicien: il suivrait alors par exemple une unité de thermique industrielle (...) — le deuxième, professeur de physique (B. SCHWARTZ, Réflex. prospectives, 1969, p. 21). 2. Thermicité, subst. fém., phys. Échange de chaleur entre un corps et le milieu extérieur lors d'une réaction physique ou chimique. La thermicité d'une réaction chimique est positive, négative ou nulle, suivant que cette réaction est exothermique, endothermique ou athermique (GDEL). 3. Thermiquement, adv., phys. Du point de vue thermique. Acier traité thermiquement. Le système est mécaniquement et thermiquement isolé (NIGGLI, Loi phases minér. et pétrogr., t. 1, 1938, p. 10). Ce même fluide, isolé thermiquement, continue à se détendre (Hist. gén. sc., t. 3, vol. 1, 1961, p. 277). 4. Thermisation, subst. fém., industr. alim. Traitement thermique modéré appliqué au lait de fromagerie afin de réduire sa flore microbienne et d'augmenter le rendement fromager. Contrairement à la pasteurisation, la thermisation n'a pas pour objectif de détruire la totalité des souches pathogènes (ADR.-LEGR. 1981).
Prononc. et Orth.:[ ]. Att. ds Ac. 1935. Étymol. et Hist. 1847 échelle thermique (HUMBOLDT, Cosmos: Essai d'une description phys. du monde, t. 1, p. 388). Dér., à l'aide du suff. -ique du gr.
]. Att. ds Ac. 1935. Étymol. et Hist. 1847 échelle thermique (HUMBOLDT, Cosmos: Essai d'une description phys. du monde, t. 1, p. 388). Dér., à l'aide du suff. -ique du gr.  « chaud », cf. angl. thermic (1846, v. NED). Fréq. abs. littér.:30. Bbg. DUB. Dér. 1962, p. 38 (s.v. thermicité). — QUEM. DDL t. 24, 28.
« chaud », cf. angl. thermic (1846, v. NED). Fréq. abs. littér.:30. Bbg. DUB. Dér. 1962, p. 38 (s.v. thermicité). — QUEM. DDL t. 24, 28.
 ]. Att. ds Ac. 1935. Étymol. et Hist. 1847 échelle thermique (HUMBOLDT, Cosmos: Essai d'une description phys. du monde, t. 1, p. 388). Dér., à l'aide du suff. -ique du gr.
]. Att. ds Ac. 1935. Étymol. et Hist. 1847 échelle thermique (HUMBOLDT, Cosmos: Essai d'une description phys. du monde, t. 1, p. 388). Dér., à l'aide du suff. -ique du gr.  « chaud », cf. angl. thermic (1846, v. NED). Fréq. abs. littér.:30. Bbg. DUB. Dér. 1962, p. 38 (s.v. thermicité). — QUEM. DDL t. 24, 28.
« chaud », cf. angl. thermic (1846, v. NED). Fréq. abs. littér.:30. Bbg. DUB. Dér. 1962, p. 38 (s.v. thermicité). — QUEM. DDL t. 24, 28.
thermique [tɛʀmik] adj.
❖
♦ Phys., cour. De la chaleur. ⇒ Calorifique.
1 Relatif à la forme d'énergie appelée chaleur, qui se traduit par des sensations spécifiques chez l'homme (⇒ Chaud, 2. froid), par des phénomènes physiques (effets thermiques) et à laquelle correspond la température.
a (En parlant du phénomène physique et de ses effets). || Effet thermique (ou calorifique) : émission ou absorption d'énergie, par contact, convection ou rayonnement. || Convection thermique (ou thermoconvection) : transport de la chaleur par mouvement d'un fluide (liquide ou gaz), dû à une différence de température ou de densité. || Rayonnement thermique : émission d'un complexe de radiations telles qu'elles se traduisent principalement par des effets calorifiques. || Luminescence thermique (thermo-luminescence). || Effet thermique d'un courant électrique (effet Joule) : production de chaleur dans un conducteur électrique sous l'influence de sa résistance (puissance thermique d'une résistance). || Énergie, équilibre; absorption thermique. || Bilan thermique : quantité de chaleur produite ou absorbée dans une réaction chimique, entre l'état initial et l'état final. — Les effets thermiques se traduisent par une modification de la température, par des changements d'état de la matière, par des dilatations, des rétractions, etc.
♦ Relatif à la température d'un lieu. || Régime thermique (→ Hiver, cit. 6). || État thermique de l'intérieur de la terre. ⇒ Géothermique.
♦ Unités thermiques, permettant de mesurer des différences de température, la température, l'énergie thermique (en joules, ergs, etc.). — Propriétés et applications thermiques. || Capacité thermique (on dit plutôt : capacité calorifique). || Conductance, conductibilité, conduction thermique, dans les métaux, les électrons libres sont principalement responsables de la conduction de la chaleur (comme de l'électricité); dans les gaz, la conductibilité thermique s'explique par la théorie cinétique élémentaire, à condition que le parcours libre moyen reste supérieur aux dimensions de l'enceinte. || Vibrations thermiques d'un réseau cristallin, dans les théories de la conductibilité (électrique, thermique), de l'absorption infrarouge, etc. || Diffusion thermique, dans un mélange de deux ou plusieurs fluides, un gradient de température a pour effet une répartition des molécules selon leurs masses (gradient de concentration). || Séparation des isotopes par diffusion thermique. || La conductibilité thermique d'un plasma peut être réduite dans d'importantes proportions par l'application d'un champ magnétique intense. || Isolement ou « isolation » thermique, réduction de la conductibilité thermique par ce procédé. — Neutron thermique : neutron lent, en équilibre thermique avec le milieu, possédant une énergie cinétique du même ordre que celle des molécules d'un gaz à la température ordinaire. ⇒ Thermalisation (des neutrons). — Facteur d'utilisation thermique : probabilité pour qu'un neutron thermique soit absorbé d'une manière efficace; sert, en particulier, à mesurer la probabilité pour qu'un neutron se trouve absorbé dans un matériau fissible. || Écran, bouclier thermique, dans un réacteur nucléaire.
♦ (V. 1965). Astron. || Rayonnement (ou émission) thermique : tout rayonnement produit par un corps solide, liquide ou gazeux à l'état d'équilibre. || Rayonnement thermique d'un plasma. || Rayonnement (ou émission) non thermique, produit par un corps qui n'est pas à l'état d'équilibre. || Émission non thermique d'un laser. || « La cosmologie moderne est dominée par deux découvertes remarquables qui ont été faites indépendamment en 1965 (…) la seconde est celle du rayonnement thermique cosmologique » (la Recherche en astrophysique, p. 215).
♦ Météor. || Ascendance thermique. || Courant thermique. N. m. || Un thermique.
b Cour. Qui produit de l'énergie (mécanique) par transformation de l'énergie thermique. || Moteurs thermiques, qui transforment l'énergie thermique en énergie mécanique (machine à vapeur, moteur à explosion, à réaction; → Machine, cit. 8). || Propulsion thermique. ⇒ Thermopropulsion. || Centrale (électrique) thermique, utilisant des moteurs thermiques pour produire l'énergie électrique. || Siphon thermique, fonctionnant par différence de température entre les différents points de ses branches.
0 Le transport de l'électricité est désormais possible à de grandes distances. Un réseau d'interconnexion est mis en place. Sur ce réseau, ce sont désormais les grandes centrales alignées sur les fleuves puissants (…) qui produisent plus économiquement. Les centrales thermiques au charbon, puis au fuel, puis au gaz naturel accomplissent la même fonction.
A. Fel, Géographie et Technique, in Encycl. Pl., Hist. des techniques, p. 1071.
c (Effets psychophysiologiques). Qui concerne la sensation de chaleur. || Sensation, sensibilité thermique : sensibilité générale superficielle de chaud et de froid. || Impression (→ Excitabilité, cit. 3), stimulation thermique.
d Techn. Qui fonctionne par effet thermique. Inform. || Imprimante, impression thermique (sur papier thermosensible).
2 Didact. Qui concerne l'étude des phénomènes thermiques. || Science thermique. || Analyse thermique : enregistrement continu, en fonction du temps, de la variation de température d'un système. || Analyse thermique d'un changement d'état, d'une transformation allotropique, d'une réaction chimique. || Analyse thermique différentielle.
♦ N. f. Vx. || La thermique. ⇒ Thermodynamique.
❖
DÉR. Thermicien, thermicité, thermiquement, thermisation, thermisé.
COMP. Suprathermique.
Encyclopédie Universelle. 2012.