Akademik

к л а с с и ч е с к а я.

Классическая Э.- область физики, в к-рой изучаются классические (неквантовые) свойства эл.-магн. поля и движения электрич. и (гипотетич.) магн. зарядов, взаимодействующих друг с другом посредством этого поля. Одна из наиболее развитых областей физики, Э. представляется широким набором различных постановок задач и их характерных решений, приближённых методов и частных случаев, объединённых общими исходными законами и ур-ниями. Последние, составляя главную, центральную часть классической Э., подробно рассмотрены в Максвелла уравнениях. В настоящей статье излагаются лишь основные принципы Э., скелет её построения и периферийные отношения с др. областями физики, так или иначе граничащими с Э.

Исходные представления

Основы Э. заложены в 18-19 вв.: сначала в пределах электростатики, магнитостатики и токовой статики, а затем- после открытия явлений магн. действия электрич. токов X. Эрстедом (Н. Oersted, 1820) и эл.-магн. индукции М. фарадеем (М. Faraday, 1831) - на базе исследований эл.-магн. взаимодействий зарядов и токов. Ур-ния для взаимосвязанных электрич. и магн. полей, возбуждаемых источниками (зарядами и токами), найдены Дж. Максвеллом (J. Maxwell, 1864-73) и стали общепринятыми после обнаружения эл.-магн. волн Г. Герцем (Н. Hertz, 1888). В результате Э. слилась с оптикой. Формирование принципов Э. в осн. завершилось в нач. 20 в. Были открыты дискретные электрич. заряды - отрицательно заряженный электрон (Дж. Дж. Томсон, J. J. Thomson, 1897) и положительно заряженные ядра атомов (Э. Резерфорд, Е. Rutherford, 1903-11). На основе ур-ний Максвелла и ур-ний Ньютона с силой Лоренца развиты представления об электронном строении вещества и в ходе анализа Э. движущихся сред построена спец. теория относительности. Она естеств. образом (с позиций классич. Э.) объяснила релятивистские оптич. эффекты и отвергла необходимость существования эфира для распространения эл.-магн. волн.

В дальнейшем фундам. исследования в Э. переместились в квантовую релятивистскую область. В частности, только квантовая Э. объяснила устойчивость вещества, ибо по законам классич. Э. ускоренно движущиеся электроны в атомах должны были бы непрерывно растрачивать энергию на излучение и в конце концов упасть на ядра. Вместе с тем при учёте квантового характера движения нерелятивистских заряж. частиц, составляющих материальные тела, законы классич. Э., описывающие взаимодействие этих частиц посредством классич. полей, позволяют объяснить подавляющую часть происходящих вокруг нас явлений. Сюда относятся не только электрич., магн. и оптич. свойства твёрдых тел, жидкостей и газов, но и их др. макроскопич. характеристики (упругость, теплопроводность, поверхностное трение, вязкость и т. д.).

В Э. прежде всего рассматриваются свободные заряды и системы зарядов, удовлетворяющие приближению непрерывного энергетич. спектра. Классическому, неквантовому, описанию их эл.-магн. взаимодействия благоприятствует то, что оно, в отличие от слабого и сильного взаимодействий, является эффективным уже в низкоэнер-гетич. пределе, когда энергия взаимодействия частиц и фотонов мала по сравнению с энергией покоя электрона. В таких ситуациях, как правило, отсутствуют рождение и аннигиляция заряж. частиц, а имеет место лишь постепенное изменение состояния их движения в результате обмена большим кол-вом низкоэнергетич. фотонов. Однако и при высоких энергиях частиц в среде (в условиях их постоянного рождения и аннигиляции, напр. в электрон-позитронной плазме), несмотря на существ. роль флуктуации, Э. может быть с успехом использована для описания среднестатистич., макроскопич. характеристик процессов.

Исходными в Э. являются следующие понятия, вводимые на основе анализа физ. измерений: геометрия рассматриваемой области пространства-времени, включая условия на её границе и гравитац. фон (пустота); заряды частиц и токи, связанные с их движением (вещество); эл.-магн. поле; силы, испытываемые частицами; пространственно-временное перераспределение вещества и поля (взаимодействие).

Геометрия. Пространство-время, рассматриваемое общей теорией относительности (ОТО), четырёхмерно и может иметь сложную топологию, напр. благодаря чёрным дырам. Его локальная геометрия является геометрией Минковского и характеризуется метрич. тензором g_ab(x^v), определяющим квадрат дифференциала расстояния ds² =g_abdx^adx^b. между бесконечно близкими точками х ^v и x^v + dx^v и являющимся ф-цией координат x^v = (ct, r). Здесь t - время, r = (х ⁱ)- пространственный 3-вектор с декартовыми координатами х ⁱ(i= 1, 2, 3), греч. индексы a, b, v= 0, 1, 2, 3. В принципе, как показывает эффект Казимира, наличие к.-л. границ и сама форма рассматриваемой области пространства могут влиять на эл.-магн. проявления вакуума в ней.

В Э. метрика пространства-времени и пространственно-временные системы координат событий, т. е. свойства гра-витац. фона, обычно (для простоты) считаются не зависящими от эл.-магн. полей и движений заряж. вещества. Самосогласование Э. и ОТО, в принципе, осуществляется совместным решением связанных ур-ний Максвелла и ур-ний Эйнштейна, учитывающих кривизну пространства-времени и её изменение вследствие перераспределения энергии-импульса эл.-магн. поля и вещества. [Существуют многочисл. теоретич. попытки связать эл.-магн., слабое и сильное взаимодействия и само возникновение соответствующих зарядов частиц с топологич. и метрич. особенностями так или иначе расширенного пространства-времени, представляющегося многомерным, напр. 10- или 11-мерным, но обнаруживающего "лишние", "скрытые" измерения только для малых, напр. планковских, длин (~10^-33 см) или для сверхвысоких энергий частиц (см. Великое объединение, Калуцы - Клейна теория, Единая теория поля).]

Относительность описания. Опираясь на релятивистскую ковариантность законов физики и идею близкодействия зарядов посредством поля (см. Взаимодействие), можно ограничиться формулировкой локальных, дифференц. ур-ний Э. в одной, удобнее всего - в к.-л. инерциальной (декартовой) системе координат ( системе отсчёта). В соответствии с эквивалентности принципом Эйнштейна описание физ. явлений представляется наиб. простым именно в локально инерциальной системе отсчёта, к-рая может быть реализована в окрестности любого события (точки пространства-времени), будучи связанной со свободно "падающим" телом отсчёта. Тогда локально тяготение не проявляется: метрич. тензор g_ab. сводится к диагональному h_ab с сигнатурой (+ - - -) (плоское Минковского пространство-время). Согласно относительности принципу, описание любых, в т. ч. эл.-магнитных, процессов не зависит (численно) от выбора различных инерциальных систем отсчёта, если в каждой из них начальные и граничные условия заданы одинаково (численно). Вместе с тем характеристики одного и того же процесса, конечно, выглядят по-разному из разл. систем отсчёта, поскольку ему отвечают в них различные начальные и граничные условия для полей и частиц.

Заряд и сила. Существенно, однако, что величина элек-трич. заряда тел (частиц) не зависит не только от выбора системы отсчёта (даже неинерциальной), но и от скорости движения тела (инвариантность заряда). Это положение исходит из следующего совместного определения элек-трич. заряда q, электрического Е и магнитного В полей, утверждающего в качестве основополагающего физ. закона (основанного на всей совокупности эксперим. данных Э.) ф-лу для силы Лоренца (в рамках идеализации точечного заряда, движущегося с определённой скоростью v):

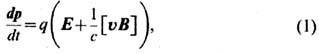
или

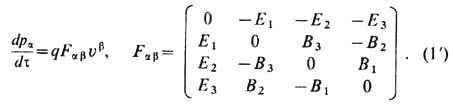
Здесь p =gmu-- импульс заряж. тела с массой покоя m, фактор g= 1/ 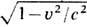, p_a=mcu_a - ковариантный вектор энергии-импульса (4-импульс), u_a=g_abu^b,u^b 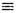дx^b/дt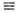(g с, gu)- контравариантная 4-скорость, 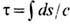- собств. время тела, определяемое длиной его мировой линии x^b(t), dt =gdt. (Здесь и далее используется Гаусса система единиц. )Инвариантность заряда экспериментально проверяется возможностью описать кинематику его движения в заданных полях в любых системах отсчёта и для любых нач. скоростей, используя, согласно (1), одну и ту же величину q (точнее, q/т), определяющую эффективность ускорения заряда. Сравнение зарядов тел q_n, п=1,2, .... производится, напр., путём измерения отношения сил F_n = q_nE, действующих на неподвижные заряды (в одном и том же поле Е). За единицу электрич. заряда принимается такой заряд, к-рый в вакууме под действием равного себе заряда на расстоянии r =1 см от него испытывает силу в 1 дин (согласно Кулона закону, величина силы взаимодействия двух неподвижных точечных зарядов равна q₁q₂/r²). Квантование заряда, т. е. его кратность величине заряда электрона е = 4,8•10^-10 ед. СГС, или е/3(кварки), в Э. вводится как дополнит. наблюдат. факт. Так, экспериментально установлено, что величина заряда протона равна заряду электрона с относит. погрешностью <=10^-21 .

Аналогичным образом, согласно (1) или (1'), с заменой скорости 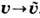, полей Е В и В- Е, атакже скалярного заряда q на псевдоскаляр 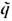(для сохранения пространственных чётности Е и нечётности В), можно ввести дуальную силу Лоренца 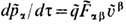и определить точечный магн. заряд 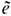. Здесь

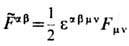
есть дуальный (антисимметричный) псевдотензор эл.-магн. поля, e^abmv- Леви-Чивиты символ. Используя идею калибровочной инвариантности, П. Дирак (P. Dirac) в 1931 показал, что элементарный магн. заряд 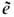должен быть тоже квантован и связан с соответствующим элементарным электрич. зарядом, 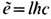/2 е, l=0, +1, +2,... (см. Магнитный монополь). Реальные магн. заряды в природе не обнаружены.

Поле. Ф-ла (1) одновременно даёт и определение клас-сич. эл.-магн. поля. С этой целью в каждой точке необходимо измерить ускорения, по крайней мере, трёх пробных частиц (с известными зарядами и массами), напр. одной первоначально покоившейся (для нахождения компонент вектора напряжённости электрич. поля Е )и двух движущихся в ортогональных направлениях (для нахождения компонент псевдовектора индукции магн. поля В). Согласно Лоренца преобразованиям, компоненты векторов сил и, следовательно, электрич. и магн. полей меняют свои значения при переходе из одной ("штрихованной") инерц. системы отсчёта в другую, относительно к-рой первая движется со скоростью и:

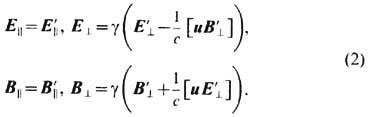
Здесь индексами || и | отмечены компоненты полей соответственно вдоль и поперёк вектора скорости u; g = = 1/ 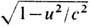. Т. о., разделение поля на электрическое и магнитное зависит от выбора системы отсчёта. Поэтому удобно использовать единый (антисимметричный) тензор эл.-магн. поля F_ab (в 1'); тогда при преобразованиях Лоренца х^a =L^a_b х'^b закон трансформации полей (2) записывается в виде F_ab= L^m_aL^v_bF'_mv. Вместе с тем инвариантными остаются две, и только две (в вакууме), алгебраич. комбинации полей:

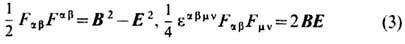
(см. Инварианты электромагнитного поля).

Динамика зарядов. Для заданных внеш. полей ф-ла (1) позволяет полностью описать движение любой системы зарядов. Однако задача значительно усложняется при учёте взаимодействия зарядов посредством создаваемого ими поля, к-рое имеет конечную скорость распространения и обладает собств. динамикой. В частности, взаимодействие любых двух произвольно движущихся зарядов не является центральным и не подчиняется третьему Ньютона закону механики, а энергия системы заряж. тел благодаря их эл.-магн. взаимодействию зависит от состояния поля и не равна сумме энергий каждого из тел в отдельности. Система заряж. тел подчиняется законам сохранения энергии, импульса и момента импульса только при учёте соответствующих величин, связанных с эл.-магн. полем (см. ниже).

Ток. В Э. для описания генерации поля точечными элек-трич. зарядами q_n, движущимися по траекториям r_n(t), используют понятия о плотности заряда r и плотности тока j:

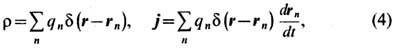
где d-дельта-функция Дирака. Отвлекаясь от точечности зарядов при наличии большого их числа (приближение сплошной среды), вводят плотность r_m = dq_m/dV и плотность тока j_m =r_mdr_m/dt сгустка зарядов dq_m сорта т, движущихся в физ. бесконечно малом объёме dV по мировой линии x^a_m(t) = (ct, r_m(t)). Дальнейшее суммирование по всем скоростям dr_m/dt зарядов, проходящих через объём dV в окрестности точки r в момент времени t, приводит к полному 4-вектору плотности тока, характеризующему упорядоченное движение зарядов:

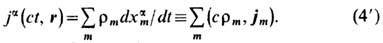
Он удовлетворяет ур-нию непрерывности j^a_,a = 0 (запятая с индексом a обозначает д/дх^a), к-рое является локальным выражением заряда сохранения закона. Согласно послед-нему, полный заряд 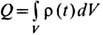в к.-л. объёме V, ограниченном замкнутой поверхностью S, не меняется, если заряды не пересекают эту поверхность. [Аналогичные утверждения распространяются на магн. заряды и их 4-псевдовектор плотности тока .]

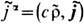Следует отметить, что излагаемая здесь последовательность согласования "правил" физ. измерения электродина-мич. величин и ур-ний Максвелла не является единственно возможной. Для Э. принципиальна лишь возможность такого согласования.

Особенности динамики поля с источниками

Согласно эксперим. данным, поток электрич. поля Е через S пропорционален суммарному заряду в объёме V:

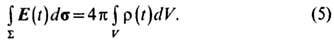
Для неподвижных зарядов это утверждение следует из закона Кулона, но в Э. справедливо и при произвольном движении зарядов внутри поверхности S, несмотря на существование излучения. Тем самым устанавливается (и экспериментально подтверждается) фундам. свойство заряда Q, к-рое может служить новым способом его измерения, формально независимым от старого (1) и не апеллирующим к кинематике заряда.

Этот шаг однозначно определяет ур-ния Э. Действительно, формулировка (5) в дифференц. форме и требование её релятивистской ковариантности, т. е. выполнения при любой скорости движения инерциальной системы отсчёта с учётом преобразований координат, поля, плотностей заряда и тока, приводят к следствию

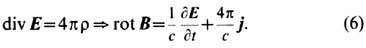
В результате магн. поле можно рассматривать как неизбежный релятивистский результат движения электрич. зарядов (тока j) и нестационарности создаваемого ими электрич. поля (тока смещения д E/дt).

Аналогичная аргументация по отношению к закону сохранения (в частности, отсутствия) магн. зарядов даёт закон эл.-магн. индукции:

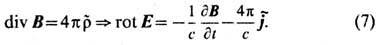
С учётом ур-ний непрерывности j^a_,a= 0 и 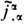=0 независимыми оказываются только правые ур-ния в (6) и (7). (Об их записи в интегр. форме, о граничных и нач. условиях, условиях излучения и о единственности решения см. Максвелла уравнения. )Полевые ур-ния (6), (7) совместно с ур-ниями движения всех зарядов под действием силы Лоренца лежат в основе Э. В релятивистски ковариантной форме ур-ния (6) и (7) имеют вид:

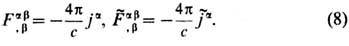
Т. о., электрич. и магн. 4-плотности тока являются локальными источниками полей. Поле, порождённое движущимися зарядами, согласно (8), распространяется в свободное от них пространство независимо от источников с одной и той же скоростью с (рис. 1). Она не зависит также от выбора инерциальной системы отсчёта ввиду явной ковариантности (8). Тем самым Э. предоставляет фактич. основу для второго постулата спец. теории относительности, требующего существования инвариантной скорости распространения сигналов.

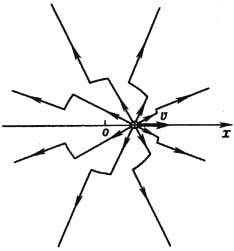
Рис. 1. Силовые линии электрического поля Е заряда q, начавшего двигаться из точки о со скоростью u.

Источники. Вместе с тем скорость u движения зарядов как источников поля в ур-ниях Максвелла формально может быть любой, в частности превышающей скорость света в вакууме [О. Хевисайд (О. Heaviside), 1889; У. Том-сон (W. Thomson), 1901; А. Зоммерфельд (A. Sommerfeld), 1904]. Последняя возможность может быть обеспечена (даже если не иметь в виду гипотетич. тахионы )совокупным движением реальных зарядов под действием разл. "зайчиков", напр. плоских импульсов фотонов, электронов или др. частиц, наклонно падающих на плоский экран, либо под действием "ножниц", где роль "зайчика" играет точка пересечения образующих "ножницы" двух лезвий. В силу неравенства u>c создаваемое "зайчиком" пятно зарядов с плотностью r может отвечать сколь угодно большой плотности тока j = ru.

В подобных и др. случаях, когда движение определённых зарядов допустимо считать заранее известным, в правых частях ур-ний (8) или (6), (7) аддитивно выделяют т. н. сторонние источники j^a _ст= (cr _ст, j _ст) и 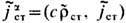-- заданные в пространстве-времени - 4-плотности тока, для к-рых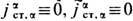

Ограничения. Границы применимости Э. в зависимости от анализируемых реальных ситуаций и преследуемых целей могут определяться самыми различными причинами. Ниже указаны лишь наиболее типичные из них.

Важнейшим свойством ур-ний Максвелла является их линейность: поля, созданные двумя независимыми системами источников j^a_1ст,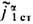и j^a_2cт,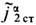, подчиняются суперпозиции принципу, т. е. сумма этих полей является решением ур-ний при совместном действии источников: j^a _ст=j^a_1ст+j^a_2ст, 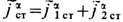. Нарушение принципа суперпозиции полей происходит за счёт нелинейного возбуждения новых токов j^a, 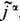, индуцируемых j^a _ст, 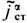при достаточно сильных полях в среде (либо в вакууме из-за квантовых эффектов рождения и уничтожения частиц, прежде всего электрон-позитронных пар, в полях |F_ab| 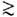Е _с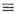 В _с = т² _е с³/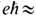4,4^.10¹³ Гс). Согласно квантовой электродинамике, вследствие рождения пар частица-античастица в достаточно сильных полях и при локализации заряж. частиц (массой т )в области с размерами порядка комптоновской длины волны 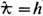/g тс возникает ограничение и на их макс. плотность тока 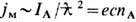Здесь I _А =g тс³/е- т . н. ток Аль-вена, отвечающий макс. концентрации 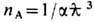частиц с зарядом е, движущихся прямолинейно друг за другом на расстоянии своего эл.-магн. классич. радиуса e²/gmc²=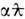. со скоростью u~c в трубке с поперечным размером ~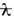; g=1/ 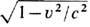, a= е ²/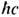. Для электронов

I_A/g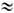17 кА.

В соответствии с неопределённостей соотношениями существуют также мин. среднеквадратичные значения полей, к-рые зависят от их частоты со и в свободном пространстве отвечают следующей спектр. плотности энергии нулевых колебаний эл.-магн. поля: [ Е²(w) + B²(w)]/8p~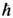(2/l)³, где l= 2p с/w. При измерении состояния полей E(ct, r), B(ct, r )как ф-ций r и t в области пространства L³ и времени Dt,aтакже при измерении их пространственно-временного среднего по этой области вследствие квантовых эффектов, обусловленных неустранимым обратным влиянием измерит. аппаратуры на поле, возникают абс. ограничения точности DE _мин = D В _мин = 2 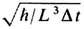[Л. Д. Ландау, Р. Пайерлс (R. Peierls), 1931] (см. также Квантовые неразрушающие измерения).

Симметрия. При локальных (точечных) преобразованиях координат и времени максимальную Ли группу симметрии, не меняющую вид ур-ний Максвелла с токами (8), составляют наряду с линейными 6-параметрич. преобразованиями Лоренца х^a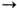x'^a =L'_b^ax^b не только очевидные 4-параметрич. преобразования сдвига х^a х'^a = х^a + а^a (см. Пуанкаре группа )и 1-параметрич. масштабные преобразования x^a х'^a = bх^a, но и нелинейные 4-параметрич. конформные преобразования (Н. Bateman, E. Cuningham, 1909)

Сопровождающие (9) конформные преобразования полей Е, В и токов j^a,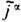. являются линейными, но явно зависят от х^a; они используются при построении нелинейных версий ур-ний Э. и нахождении их точных решений. Ур-ния Максвелла (8) не изменяются также при локальных внутренних, т. е. не затрагивающих пространственно-временные координаты, д у а л ь н ы х п р е о б р а з о в а н и я х:

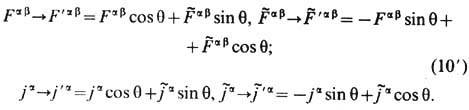
Для свободных полей они известны как 1-параметрич. п р е о б р а з о в а н и я Л а р м о р а-Р а й н и ч а

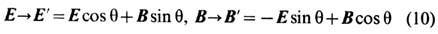
и связаны с поляризац. вырождением эл.-магн. волн. Однако преобразования (10'), как и (9), не сохраняют вид ур-ний движения (1) электрич. (или магн.) зарядов.

Магнитный заряд. Явное согласование дуальной симметрии ур-ний Максвелла и ур-ний движения имеет место только в случае дуально заряженных частиц, несущих одновременно электрич. q_n и магн. 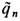заряды. Последние преобразуются в соответствии с (10') по правилу

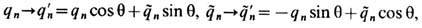
не изменяющему полную силу Лоренца, действующую на n -ю заряж. частицу:

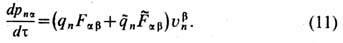
Если отношение 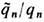равно одной и той же (любой) величине для всех частиц, то дуальный поворот на угол 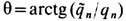приводит ур-ния Э. (8), (11) к обычной форме без магн. монополей (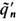=0) с наблюдаемыми эфф. электрич. зарядами частиц q'_n=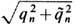и наблюдаемыми полями E', В' из (10) [Л. Пёйдж (L. Page), H. Адам (N. Adam), 1940]. Универсальность отношения 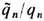для известных частиц экспериментально подтверждается с большой относит. точностью (напр., для электронов и протонов относит. погрешность не превышает ~10^-26). Это обстоятельство, позволяя исключить дуально заряженные частицы и, в частности, "чистый" магн. монополь (для к-рого отношение 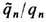по величине и по знаку должно быть обратно таковому для "чистого" электрич. заряда), скрывает дуальную симметрию однозарядовой Э. Тем не менее и в ней наиб. фундаментальными естественно считать те наблюдаемые, к-рые инвариантны относительно дуальных преобразований (а не сами электрич. и магн. поля), напр. дуально симметричную силу Лоренца (11), эфф. заряд q'_n и компоненты T^mv тензора плотности энергии-импульса эл.-магн. поля (А. Зоммерфельд, 1928):

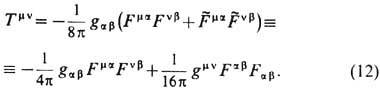
Даже в отсутствие "чистых" магн. монополей в Э. допустимы высшие магн. мультиполи, начиная с диполя, образованные магнитно нейтральной совокупностью монополей (ср. двухкварковую структуру мезонов и трёхквар-ковую структуру барионов). Однако эксперименты фактически исключают эту возможность, показывая, что все магн. мультиполи образованы электрич. токами. Так, в 1951 в экспериментах по рассеянию нейтронов в неоднородном магн. поле В= В (х) у⁰ (рис. 2) было показано

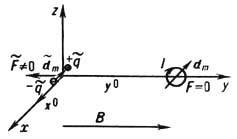
Рис. 2. Силы, действующие на "токовый" d_m и "моно польный" 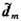магнитные диполи, ориентированные против оси х° и находящиеся в неоднородном магнит ном поле В=В(х)у°.

[К. Г. Шал (С. G. Shull) и др.], что их магн. дипольный момент d_m имеет токовую [Ю. Швингер (J. Schwinger), 1937], а не монопольную [Ф. Блох (F. Bloch), 1936] природу: нейтроны движутся под действием силы F=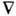(d_mB), характерной для рамки с электрич. током I=cd_m/pr₀². (радиуса r₀), но не силы 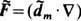В, характерной для двух . разноимённых монополей b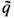= + 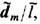расположенных на расстоянии l. При 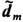=d_m различие указанных сил F-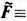.[d_mrotB]обусловлено различным взаимодействием диполей со сторонними токами j=(c/4p)rot В, создающими неоднородное магн. поле В(r).

Электромагнитная асимметрия. Т. о., вещество устроено дуально несимметрично, из одних лишь электрич. зарядов. Впрочем, по крайней мере в макроскопич. Э., это не исключает ситуации, когда в неподвижной системе проводников отлична от нуля только плотность тока (и соответствующие магн. и тороидные мультипольные моменты), тогда как плотность электрич. заряда тождественно равна нулю. Создаваемое такой системой электрич. поле Е отлично от нуля, только если токи нестационарны. При движении относительно этой системы наряду с плотностью тока в ней будут наблюдаться плотность заряда и соответствующие электрич. мультипольные моменты; однако не существует системы отсчёта, из к-рой наблюдалась бы одна только плотность заряда и не наблюдалась бы плотность тока, а следовательно, всюду отсутствовало бы магн. поле.

В общем случае, согласно (7), ввиду отсутствия магн. зарядов и независимо от движения электрич. зарядов

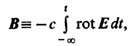
т. е. магн. поле выступает как вспомогательное, характеризующее историю эволюции основного электрич. поля. Несмотря на это, введение самостоят. магн. поля необходимо, если последовательно придерживаться идеи близ-кодействия зарядов, т. е. описывать их взаимодействие только посредством локально (а не интегрально) измеримых полевых величин.

Экстремальные принципы. В отличие от дуально симметричной Э. (8), (11), в однозарядовой Э. не возникает проблем с получением совместной системы ур-ний (1), (8) 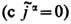для движения отд. электрич. зарядов q_n и поля в вакууме из вариац. принципа (см. Вариационное исчисление). Для удобства вводятся новые полевые переменные - скалярный j( сt, r) и векторный A(ct, r) потенциалы электромагнитного поля:

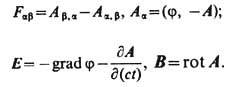(13)

Тогда второе ур-ние из (8), принимающее вид F_ab,v + F_va,b+ +F_bv,_a = 0, и, следовательно, ур-ния (7) с 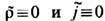удовлетворяются тождественно. Первое же ур-ние из (8) и ур-ние (1') с учётом (4') [или ур-ния (6) и ур-ние (1) с учётом (4)] есть в точности Эйлера - Лагранжа уравнения с лагранжианом

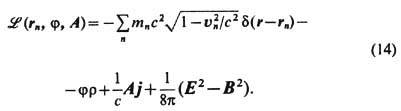
При этом, правда, в последнем слагаемом необходимо исключить бесконечную энергию собственного (кулонов-ского) поля точечных зарядов, а в слагаемом взаимодействия A_aj^a/c- самовоздействие зарядов. Поскольку наблюдаемая масса заряж. частиц т _n конечна, компенсацию их бесконечной эл.-магн. массы следует обеспечить введением бесконечной отрицат. массы неэлектромагн. происхождения ("перенормировка" массы). Эта непоследовательность, связанная с идеализацией точечных элементарных частиц, в релятивистской классич. физике, не включающей описание детальной внутр. структуры заряж. частиц, напр. как полевых образований, неизбежна в силу невозможности существования абсолютно недеформируемых протяжённых тел.

Калибровочная инвариантность. Если отказаться от то-чечности и учесть неэлектромагн. взаимодействие частиц, то, описывая частицы нек-рым классич. полем y, первое слагаемое в (14) следует заменить на более общий лагранжиан частиц 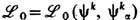, зависящий от к.-л. многокомпонентных комплексных ф-ций yk(x^a), k=1, 2, ... , и их производных y^k_,a. С учётом вещественности 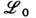требование инвариантности полного лагранжиана относительно локальных фазовых преобразований

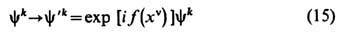
( калибровочные преобразования; 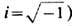обнаруживает за-мечат. факт, известный как эвристич. принцип калибровочной инвариантности и перенесённый из Э. на всю теорию поля [Ч. Янг (Ch. Yang), P. Миллс (R. Mills), 1953; M. Гелл-Ман (М. Gell-Mann), 1956]. Согласно этому принципу, инвариантность исходного лагранжиана 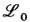восстанавливается удлинением производных

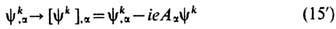
за счёт введения компенсирующего поля A_a( х^b), преобразующегося одновременно с (15) по т. н. калибровочному закону

не меняющему наблюдаемые компоненты поля (13) F_ab. [В (15') величина заряда электрона е выступает как константа введённого таким образом взаимодействия - мин. эл.-магн. взаимодействия,- давая ещё одно неявное определение электрич. заряда.] Если для определённости ограничиться линейной зависимостью 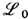от производных y^k_,a, характерной для спинорных полей вещества, то в полном лагранжиане

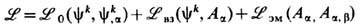
непосредственно возникает необходимый лагранжиан взаимодействия 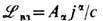вместе с новым определением 4-плотности тока 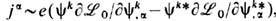, не связанным с точечностью зарядов [ср. (4), (14)].

Собственный лагранжиан компенсирующего (здесь - эл.-магнитного) поля выбирается в простейшем виде 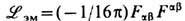[см. (3), (13)], обеспечивающем его инвариантность при калибровочном преобразовании (15 ") в отсутствие вещества. Этим, в частности, исключается слагаемое вида 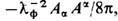а следовательно, возможность ненулевой массы фотона 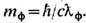Наличие ненулевой массы фотона кардинально меняло бы законы Э. на расстояниях 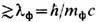[Л. де Бройль (L. de Broglie), 1924]; однако земные эксперименты, в частности по проверке закона Кулона и независимости скорости эл.-магн. волн в вакууме от их частоты, допускают такую возможность только на расстояниях 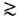10¹⁰ см, а наблюдения стабильных конфигураций газа и магн. полей галактик - на расстояниях 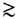10²² см. В принципе было бы возможно также несохранение электрич. заряда, напр. распад электрона на нейтральные частицы или осцилляции электрон <-> позитрон, хотя подобные процессы и подавлены неизбежным участием большого кол-ва (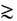10¹³ -10²¹) сверхмягких продольных фотонов (Я. Б. Зельдович, Л. Б. Окунь, М. Б. Волошин, 1978); однако лабораторные эксперименты и глобальные геоэлектрич. оценки показывают, что время жизни электрич. заряда превышает 10³⁰ с.

Внутренние противоречия (неклассические проблемы)

Нелинейность. Включение в лагранжиан эл.-магн. поля неквадратичных по E и В слагаемых ведёт к нелинейной теории. Наиб. известное нелинейное обобщение Э. развито В. Гейзенбергом (W. Heisenberg), Г. Эйлером (Н. Euler), В. Вайскопфом (V. Weisskopf) (1936) и Ю. Швингером (1951) на основе квантово-электродинамич. вычисления поляризации электрон-позитронного вакуума, создаваемой достаточно плавными в пространстве-времени полями, для к-рых удаётся использовать точное решение Дирака уравнения. Соответствующий лагранжиан, для простоты выписываемый в естеств. единицах (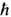=с= 1),

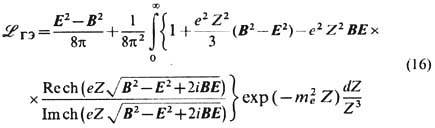
описывает только эл.-магн. поле, причём плавно неоднородное, в пренебрежении производными от инвариантов (3). Он не претендует на самосогласованное "эл.-магн." описание источников поля - электронов и позитронов с зарядами + е и конечной классич. массой т _е, как это предполагалось в нек-рых моделях, напр. М. Борном (М. Born) и Л. Инфельдом (L. Infeld) (1934), выбиравшими лагранжиан в виде

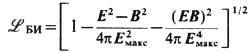
(впрочем, более реалистичном с точки зрения совр. струн теории; Е. С. Фрадкин, А. А. Цейтлин, 1985). Здесь E _макс -нек-рое макс. поле. Мнимая часть (16) характеризует неустойчивость вакуума, точнее, вероятность рождения электрон-позитронных пар в единичном объёме за единицу времени, значительную при 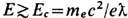и убывающую по закону ехр(-p Е _с/Е )в полях Е<<Е _c. Вещественная часть (16) отвечает за собственную нелинейность "классич." электрон-позитронного вакуума-в отсутствие др. частиц и др. взаимодействий, к-рые, конечно, кардинально меняют ситуацию, скрадывая чисто эл.-магн. взаимодействие, начиная с расстояний ~10^-13 см (сильное) и особенно ~ 10^-16 см (электрослабое).

Если, несмотря на сказанное, обратиться, напр., к модификации закона Кулона, т. е. к сферич. симметрич. решению D = q/r² соответствующих (16) электростатич. ур-ний Максвелла div D =0 (при r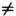0), 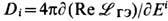, с сингулярностью (точечным зарядом q )в начале координат r = 0, то обнаружится принципиальная роль нелинейности вакуума:

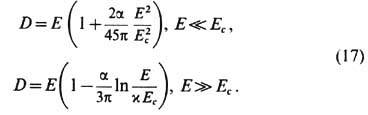
Здесь число 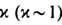учитывает все члены первого порядка по постоянной тонкой структуры 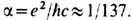Согласно (17), на больших расстояниях поле Е ослабляется по сравнению с g/r²: D/E >1, т. е. поляризов. вакуум экранирует "голый" заряд q. Однако на малых расстояниях эта экранировка уменьшается, и поляризация вакуума меняет знак при 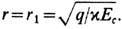На меньших расстояниях возникает антиэкранировка, причём отношение D/E принимает мин. значение a/3pпри

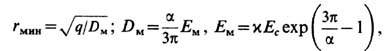
когда ф-ция D(E )достигает максимума и обнаруживающаяся двузначность ф-ции Е(r )делает физически бессмысленным анализ области r<r _мин. Хотя сама квантовая Э. как асимптотическая по a теория вряд ли верна на расстояниях r<<r _мин, апри r~r _мин указанное решение ввиду пространственной неоднородности заведомо выходит за квантово-электродинамич. рамки применимости лагранжиана (16), утверждение о том, что в нелинейной Э. (даже без учёта рождения реальных электрон-позитронных пар) должны существовать макс. электростатич. поле Е _м и аналогичное макс. магнитостатич. поле В _м = В _с ехр (3p/a - 1), представляется неизбежным, поскольку остаётся справедливым и для пространственно однородного поля, напр. в плоском конденсаторе или в соленоиде [М. Гринман (М. Greenman), Ф. Рорлих (F. Rohrlich), 1973; Д. А. Киржниц, А. Д. Линде, 1978]. Это ещё раз показывает, что наивные представления о точечности заряда, напр. электрона, отвечающие неограниченному при r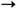0 кулоновскому полю е/r², противоречивы, причём не только в Э., но и в квантовой Э. (Л. Д. Ландау, И. Я. По-меранчук, Е. С. Фрадкин, 1955). Наблюдаемая величина (и масса) заряда так или иначе должна определяться самосогласованными свойствами поляризов. вакуума с учётом неэлектромагн. взаимодействий, "размазывающих" точечный заряд.

Классический размер частиц. При этом в любой, в т. ч. квантовой, теории, отвлекающейся от неэлектромагн. структуры заряда, введение представлений о нелокальном взаимодействии поля с протяжённой заряж. частицей как единым целым наталкивается на значит. трудности, прежде всего причинного характера. В Э., пусть линейной (14), подобные попытки, несмотря на содержательность, также оказываются ограниченными. Среди них наиб. популярно представление о распределении заряда электрона по области размером ~r _е = е ²/т _е с²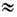3^.10^-13 см ( классический радиус электрона), что соответствует приписыванию, хотя бы частичному, энергии покоя электрона т _е с². его кулоновскому полю. Это представление, конечно, предполагает наличие к.-л. неэлектромагн., упругих сил (т. н. н а т я ж ен и й П у а н к а р е), к-рые препятствуют кулоновскому расталкиванию "частей" электрона и обеспечивают релятивистскую ковариантность его полного 4-импульса, складывающегося из нековариантных 4-импульсов поля "электрич. начинки" и натяжений "упругого теста". Анализ устройства натяжений Пуанкаре выходит за рамки Э. не только из-за неизбежности квантового подхода, но даже потому, что внутри такого электрона они благодаря классич. эффектам гравитации, по-видимому, обусловливают наличие отрицат. плотности массы покоя [В. Боннор (W. Bonnor) и др., 1989].

Строго говоря, вследствие эффекта рождения электрон-позитронных пар применимость Э., по крайней мере без учёта сильных флуктуации заряда и эл.-магн. поля, проблематична уже на расстояниях меньше комптоновской длины волны электрона 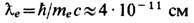(П. Дирак, 1928). Вместе с тем эксперименты с электронами и мю-онами высоких энергий показывают, что при разл. взаимодействиях с др. частицами они ведут себя как точечные вплоть до расстояний ~10^-16 см.

Реакция излучения (радиационное трение). Принимая тем не менее к.-л. распределение заряда, напр. равномерное внутри шара радиуса r _е, на основе Э. можно ответить на важнейший вопрос о результате эл.-магн. воздействия разл. "частей" электрона друг на друга. Оказывается, несмотря на то, что эл.-магн. масса зависит от выбранного распределения, от него не зависит самовоздействие электрона, т. е. полная сила реакции излучения [X. Лоренц (Н. Lorentz), 1892; М. Абрагам (М. Abragam), 1904]

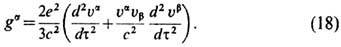
Она получается после перенормировки массы в первом порядке разложения по малому отношению r _е к характерному масштабу неоднородности поля (или малому параметру запаздывания e²/m_ec³t). Независимость (18) от r _е обеспечивает корректность учёта самовоздействия в пределе точечного заряда r _е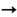0. При этом обычно требуется условие малости силы g^a по сравнению с силой Лоренца (1') со стороны внеш. поля. Оказывается, что последнее условие достаточно выполнить в системе отсчёта, где электрон покоится и сила реакции излучения на него равна g=(gⁱ/c) =(2e²/3c³)d²u/dt². Для гармонич. полей Е, В с частотой w оно даёт ограничения (условия внутр. непротиворечивости Э.)

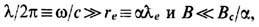
к-рые в a^-1 = 137 раз слабее, чем-приведённые выше квантово-электродинамич. ограничения. Второй закон Ньютона для изменения 4-импульса тсu^a точечного заряда, находящегося под действием "обычной" внешней силы (1') и "необычной" силы Лоренца-Абрагама (18), к-рая сама определяется кинематикой заряж. частицы, можно представить в более традиционной форме

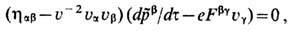
если ввести понятие "эл.-магн." комплекса с эфф. 4-им-пульсом

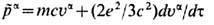
[К. Тейтелбойм (С. Teitelboim), 1970]. Последний указывает на неразделимость заряда и его собственного ближнего поля (эл.-магн. шубы). Это "связанное" поле автоматически учитывается в локальном балансе 4-импульсов, следующем из приведённого второго закона Ньютона: приращение 4-импульса комплекса и создание 4-импульса "свободного" поля излучения происходят за счёт поглощения 4-импульса внешнего поля.

Непротиворечивое введение самовоздействия путём добавления силы (18) к силе Лоренца (I) для каждого точечного ускоренно движущегося заряда q_n в рамках Э. предполагает дополнит, условие отсутствия ускорений в областях вне поля, E=B=0. в (1). Иначе в получающихся ур-ниях движения, содержащих теперь третьи производные координат частиц r_n по времени, могли бы появиться неприемлемые решения, отвечающие неогранич. самоускорению заряда за счёт бесконечной энергии собственного поля. Разумеется, упомянутый выше "одетый" эл.-магн. комплекс вообще не испытывает самоускорения, поскольку в любой мгновенно сопутствующей системе отсчёта для перенормированного импульса 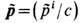справедливо ур-ние (1). Автоматич. отбор физически приемлемых решений ур-ний движения "голой" заряженной частицы, независимо от соотношения между силой реакции излучения и силой Лоренца, возможен также при их формулировке в эквивалентном интегральном виде, включающем начальные и конечные условия (Ф. Рорлих, 1961), Так, рассматривая (для простоты) нерелятивистский случай [Д. Д. Ива-ненко, А. А. Соколов, 1948; Р. Хааг (R. Haag), 1955], при конечном условии du/dt=0 (при 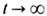) имеем

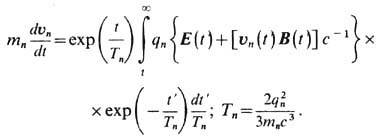
Здесь налицо формальное нарушение причинности, поскольку ускорение выражается не через прошлое, а через будущее движение частицы, т. е. определяется полями, до к-рых частица ещё не дошла, на временном интервале ~ Т _n. Однако для всех заряж. частиц (тел) времена Т _n =2r _п/3 с<= Т _е=2 е²/(3 т _е с³)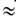6^.10^-24 с и, следовательно, все соответствующие проблемы непричинности и нелокальности эл.-магн. взаимодействия оказываются за пределами применимости Э. А именно, принципиальным становится учёт квантовых флуктуации движения электрона (или любой заряж. частицы), для к-рых характерный временной, 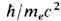, и пространственный, 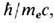масштабы в 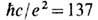раз больше соответственно временного, Т _е, и пространственного, сТ _е, масштабов самоускоряющихся решений. Эти проблемы корректно разрешаются при кван-тово-электродинамич. анализе самовоздействия [Е. Мо-ниц, Д. Шарп (Е. Moniz, D. Sharp), 1977; В. К. Кривицкий, В. Н. Цытович, 1991 ]. Оказывается, что при достаточно длительном действии сила реакции излучения действительно проявляется на классич. уровне, напр., она обусловливает спиральное (скручивающееся) движение электронов в однородном магн. поле, отличающееся от винтового движения с постоянным радиусом благодаря трению о собственное синхротронное излучение.

Запаздывание. Причинности принцип играет в Э. важнейшую роль, поскольку, согласно условиям излучения (при постановке нач. задачи в ограниченной области пространства), он требует ограничиться только запаздывающими решениями ур-ний Максвелла, нарушая их обратимость во времени (при замене j 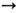-j,rr, В- В, Е-> Е Если для определённости выбрать условие калибровки Лоренца A^a_,a= 0, то вынужденное решение соответствующего (8) волнового ур-ния А^a,b_,b = 4pj^a/ с для системы точечных зарядов можно записать в виде

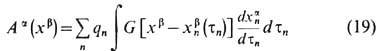
( Льенара - Вихерта потенциалы). Здесь интегрирование ведётся по собств. времени т„ каждой из заряж. частиц и использована запаздывающая Грина функция G(х^m )отличная от нуля только в световом конусе будущего ( х⁰>0) и равная там 2d (- х_m х^m )(для свободного пространства). Из решения (19) вытекают, по существу, все результаты Э. об излучении и взаимодействии зарядов; для пространственно ограниченных задач в нём необходимо лишь соответствующим образом изменить ф-цию Грина.

Дальнодействие. Можно совсем не вводить распределённое в пространстве поле, а подставить его явные значения в точках нахождения зарядов в ур-ния их движения. Тогда Э. примет вид теории прямого межчастичного взаимодействия с ф-цией Лагранжа, зависящей только от координат и скоростей зарядов [X. Тетроде (Н. Tetrode), 1922; А. Фок-кер (A. Fokker), 1929]. Для такой переформулировки Э. в решении (19) удобнее использовать непричинную ф-цию Грина, всюду определяемую полуразностью запаздывающего и опережающего потенциалов:

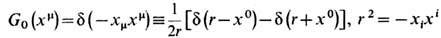
(для свободного пространства). В полевой трактовке этим учитывалось бы "свободное" поле излучения и снималась бы проблема самовоздействия и перенормировки массы в пределе точечных зарядов (П. Дирак, 1938). Вместе с тем добавлением к получающейся ф-ции Лагранжа полных производных по времени удаётся придать новой теории явно причинную форму, причём симметричную по перестановкам частиц [Р. Муре (R. Moore), Т. Скотт (Т. Scott), М. Монахан (М. Monahan), 1988]. В частности, для заряда q_k, взаимодействующего со всеми остальными зарядами Вселенной, ф-ция Лагранжа принимает вид:

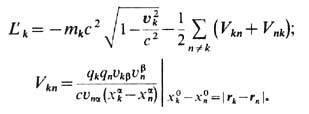
Поправка на силу реакции излучения (в нерелятивистском случае)

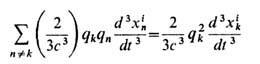
к запаздывающей силе Лоренца, 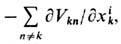обусловлена одними и теми же (остальными, п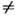k )зарядами Вселенной и возникает в уравнении движения 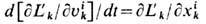естеств. образом из требования самосогласованности движения всех заряж. частиц при условии квазинейтральности Вселенной и отсутствия элек-трич. поляризации при усреднении по всем рассматриваемым зарядам, 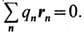Здесь проблема самоускорения

заряда не возникает, поскольку отсутствует внутренний бесконечный источник энергии (собственное кулоновское поле), и без силы Лоренца невозможно появление "силы реакции излучения", автоматически низведённой на роль поправки.

Что касается свойств необратимости во времени и выделения обычных запаздывающих решений, то они связываются со свойствами эволюционирующей материи и всей Вселенной и ввиду наличия неэлектромагн. сил выходят за рамки Э., требуя включения дополнит. физ. постулатов [Дж. Уилер (J. Wheeler), P. Фейнман (R. Feynman), 1945; Д. Пегг (D. Pegg), 1975]. В целом исследования Э. как теории прямого межчастичного взаимодействия направлены на то, чтобы преодолеть внутр. противоречия полевой Э., связанные с точечностью зарядов, перенормировкой их массы, нарушением причинности при самовоздействии, ограничением макс. потенциалов и мин. расстояний взаимодействия зарядов и пр. Однако, поскольку эти противоречия затрагивают лишь область квантовых явлений, применение в области классич. физики переформулированной, неполевой Э. оказывается несколько искусственным и непопулярным, особенно вследствие её усложнённости. Последнее гл. обр. обусловлено необходимостью выделения запаздывающих координат частиц, накладывающего сложные условия связи на вариац. ур-ния теории.

Законы сохранения и ненаблюдаемость потенциалов

В полевой формулировке Э. этих сложностей нет, и в анализе взаимодействия зарядов на первый план выступает динамика самого создаваемого ими поля. Существенно, что благодаря калибровочной инвариантности в Э. нельзя непосредственно наблюдать потенциалы А^a этого поля. Такая возможность имеется только в квантовой физике и обнаруживается, напр., в интерференц. эффектах вследствие изменения фазы волновых ф-ций заряж. частиц под действием потенциалов А^a( х^b) даже в тех пространственно-временных областях, где в силу особенностей топологии отсутствуют напряжённости поля, F_ab = 0 (см. Ааронова - Бома эффект). Наблюдение потенциалов j, А было бы возможно в калибровочно неинвариантной Э. с ненулевой массой фотона, где при условии калибровки Лоренца волновое ур-ние для них имеет вид Прока уравнения А^a,b_,b -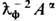=4pj^a/c ссохраняющимся 4-током (j^a_,a = 0), первое и второе ур-ния Максвелла (6) содержат в правых частях слагаемые соответственно 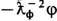и 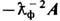, а плотности энергии эл.-магн. поля и её потока (Пойнтинга вектор )равны:

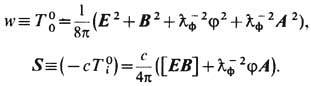
Несмотря на ненаблюдаемость при m _ф = 0, потенциалы часто используются для описания различных (калибровочно инвариантных и неинвариантных) характеристик эл.-магн. поля.

Момент импульса, спин и "масса" поля. Важные примеры первых и последних - тензоры плотности импульсного, M^v_ab = ( х_aT ^v_b -x_bT^v_a)/ с [см. (12)], и спинового, S^v_ab=(A_aF^v_b-A_bF^v_a)/4p с, моментов, определения к-рых диктуются Нётер теоремой. Им соответствуют векторы плотности момента импульса (А. И. Садовский, 1897) и спина [Ч. Г. Дарвин (Ch. G. Darwin), 1932]:

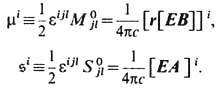
Первый лишь неявно зависит от поляризации поля, а второй непосредственно связан с ней. Их разность m-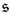, обычно заменяемая на вектор l=[r([E][ 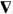А]+( Е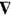) А)]/4p с, характеризует "орбитальную" часть момента импульса, к-рая, как и спиновая, зависит от калибровки. Для свободного поля здесь удобна кулоновская калибровка div A=0, позволяющая считать j=0. Тогда, поскольку T^v_a,v = 0 и F^v_a,v=0, для любой замкнутой конфигурации поля излучения, наряду с 4-импульсом Р_a=(W,- Р )и полным моментом импульса М, сохраняются во времени также спин 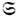и "орбитальный" момент импульса L = М-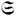. Эти величины определяются пространственными интегралами соответственно от T⁰_a = (w, - S/c),m, 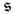и l по всей области 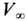, занятой полем. Ковариантность сохраняющегося 4-вектора энергии-импульса поля Р_a позволяет говорить о скорости центра "масс" поля и ⁱ = сР ⁱ/Р₀, где Р₀=W/c. Его "массу" (покоя) m₀, в общем случае переменную во времени, можно ввести ф-лой

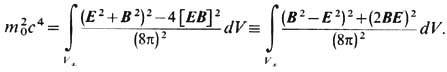
Последнее тождество в соответствии с (3) показывает релятивистскую инвариантность данного определения, причём в качестве квадрата плотности "массы" под знаком интеграла стоит квадрат L² любого из четырёх собств. значений (совпадающих по величине) тензора плотности энергии-импульса поля, T^v_aa^a_k =L_k а ^v_k. Т. о., даже при нулевой массе фотона, m _ф = 0, поле излучения может обладать "массой", m₀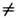0, наличие к-рой отвечает (частичной) локализации эл.-магн. энергии благодаря (частичной) параллельности векторов Е и В либо благодаря (частичному) уничтожению потока энергии при усреднении вектора Пойнтинга с [ ЕВ]/4p из-за переменности его направления в пространстве, напр. для стоячей волны.

Законы сохранения. Если с полем взаимодействует ограниченная система заряж. частиц (тел), то во времени будут сохраняться их совместные энергия-импульс и момент импульса (см. Мультиполъное излучение). Поскольку описание частиц полевым образом через y-функции выходит за рамки Э. точечных зарядов, то в ней не используется и возможность равноправного с орбитальным моментом введения спина заряж. частиц [Ф. Белинфанте (F. Belinfante), 1939], а также соответствующего магн. момента как циркулирующего течения заряда в поле y-волны [В. Гордон (W. Gordon), 1928]. Более того, утрируя ситуацию, согласно ур-нию Дирака, в Э. элементарный заряд, скажем, электрона, нельзя рассматривать иначе как точечный квант заряда е, непредсказуемо движущийся со скоростью света с (нем. Zitterbewegung - дрожание) внутри комптоновского объёма 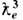так, что ср. поступат. скорость электрона совпадает с его классич. скоростью u. Аналогично в итоге усреднения возникают его спин 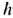/2, равный произведению ср. радиуса 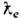/2 на импульс т _е с, и магн. дипольный момент е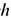/(2 т _е с), равный произведению ср. тока 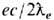на площадь 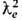и фактор с^-1 [К. Хуанг (К. Huang), 1952]. Отвлекаясь от подобных наглядных представлений, в совр. версиях Э. точечные заряж. частицы просто наделяют определёнными магнито- и электроди-польными (и высшими мультипольными) моментами и так или иначе постулируют законы их взаимодействия с эл.-магн. полем.

Игнорируя указанные мультипольные эффекты, к-рые для элементарных зарядов обычно малы по сравнению с исходными монопольными эффектами, и вводя для сиc-темы точечных зарядов тензоры

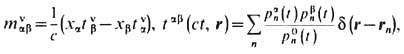
можно прийти к ур-ниям непрерывности

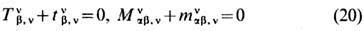
суммарных тензоров плотности энергии-импульса и момента импульса. Отсюда после интегрирования T⁰_b +t⁰_b и mⁱ + (l/2)e^ijlm_jl⁰; по всей области 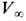, занятой полем и частицами, следуют законы сохранения их полных 4-импульса P_a + P_0a и момента импульса М+М₀. Механич. взаимодействие зарядов с полем описывается 3-плотностью 4-силы Лоренца:

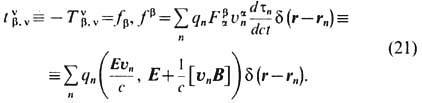
При переходе к непрерывному распределению заряда в среде рассматривают сгусток зарядов dq_n, движущихся в физ. бесконечно малом объёме dV по мировой линии x^a_n(t) = (ct, r_n(t)), и вводят плотность силы Лоренца f_n =r_nE+c^-1.[j_n В]. Изменение механич. энергии зарядов

,

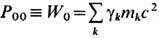находящихся внутри к.-л. области V(t), совершается работой только электрич. поля: 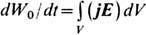. Она определяется распределением полной плотности тока 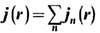по элементам объёма dV, но из теоремы Пойнтинга jE=-dw/dt - divS может быть выражена через изменение энергии эл.-магн. поля W внутри объёма V(t) и её поток через границу S (t) этого объёма, элементы к-рой da имеют локальную скорость u':

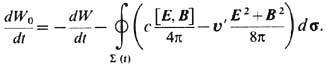
Классическая электродинамика в искривлённом пространстве-времени

До сих пор речь шла о плоском пространстве-времени (и декартовых координатах в нём). Будучи искривлённым, оно изменяет характер взаимодействия между эл.-магн. полем и заряж. частицами; такова ситуация, напр., в окрестностях вращающихся нейтронных звёзд и чёрных дыр. Нарушаются также законы Э. о сохранении полных 4-импульса Р_a + Р_0a и момента импульса М+ М₀. благодаря их передаче гравитац. полю. В частности, возможны прямая трансформация эл.-магн. волн в гравитационные и непосредств. гравитац. излучение заряж. частиц, движущихся под действием эл.-магн. поля, напр., в плазме. Считая гравитац. фон g_ab(ct, r )внешним, заданным независимо от перераспределения энергии-импульса эл.-магн. поля и зарядов, законы Э. как системы дифференц. ур-ний первого порядка можно однозначно установить из принципа общей ковариантности. Согласно этому принципу, в искривлённом пространстве-времени (или в любых криволинейных координатах) следует заменить частную производную (запятую) любого тензора, напр. 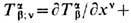T^a_b,v в (20), на ковари-антную производную (точку с запятой) 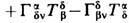, добавляя на каждый контравариантный индекс а член + 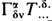, а на каждый ковариантный индекс Р член 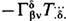, где 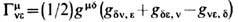-Кристоффеля символы.

В результате ур-ния Э. (Г), (8) (без магн. зарядов) суть

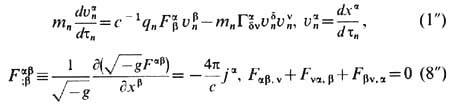
(g = det g_ab), причём последнее ур-ние не меняет свой вид и удовлетворяется введением прежних потенциалов (13). Вектор 4-тока

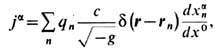
или для непрерывного распределения зарядов 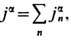где 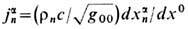[в окрестности мировой линии х _n(t)], а плотность зарядов 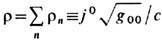. Ур-ние непрерывности T^v_b;v=-f_b для плотности энергии-импульса эл.-магн. поля (12) (и аналогично - зарядов) принимает вид

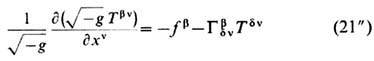
и содержит, наряду с силой Лоренца f^b [ср. (21)], силу тяготения. Последняя имеется также в ур-нии движения зарядов (1 "), куда, кроме того, нужно в качестве поправки ввести силу реакции излучения. Она включает дополнительные к (18) слагаемые, связанные с ускоренным движением заряда в гравитац. поле, в т. ч. создаваемом 4-им-пульсом эл.-магн. поля - внешнего и собственного.

Поле тяжести как среда. Электрическое Е и магнитное В поля, определяемые компонентами 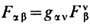, по-прежнему находятся, согласно (1 "), непосредственными измерениями ускорений пробных заряж. частиц, движущихся с определённой скоростью u^a_n в локально инерциальной (свободно падающей) системе отсчёта, где Г ^a_dv = 0 (см.

Геодезическая линия). Для записи ур-ний поля (8 ") в 3-мерной форме удобно ввести вектор G_i= -g_0i/g₀₀, 3-мерный метрич. тензор 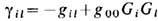, его определитель Г = det g_il и новые, отличные от E_i = F_0i и В ⁱ = =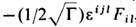, поля

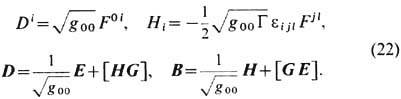
Тогда ур-ния Максвелла в гравитац. поле для произвольных локальных координат r и локального времени t принимают вид

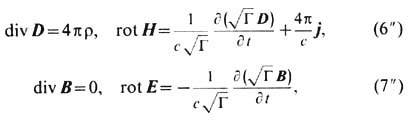
формально аналогичный ур-ниям в среде. В частности, статич. гравитац. поле играет роль среды с электрич. и магн. проницаемостями 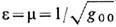, причём в слабом поле тяжести всё определяется скалярным гравитац. потенциалом j _г, поскольку 1-g₀₀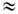2j _г/ с². Другие, иногда более удобные, формы ур-ниям (8 ") можно придать, производя "3 +1"-расщепление пространства-времени и переходя к "абсолютному" пространству и единому "глобальному" времени, но используя для измерения физ. величин F_ab и j^a систему отсчёта к.-л. локальных наблюдателей, напр. локально невращающихся [К. Торн (К. Thorne), Д. Макдональд (D. Macdonald), 1982]. Обобщая конформные преобразования (9), сохраняющие ур-ния светового конуса х_a х^a =0, можно утверждать, что ур-ния Максвелла (6 ") - (8 ") ковариантны по отношению к общему растяжению всех длин согласно замене:

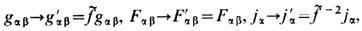
где 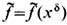-произвольная ф-ция координат.

Оптика и термодинамика излучения в гравитац. поле.

В отсутствие источников ур-ния (6 ") - (8 ") имеют наиб. простое решение для полей, длина волны к-рых мала по сравнению с характерным радиусом кривизны пространства-времени и масштабом изменения амплитуды, поляризации и длины волны этих полей. В таком приближении справедливы законы геом. оптики: световые лучи являются нулевыми геодезическими, удовлетворяющими ур-ниям g_abdx^adx^b =0; вектор поляризации поля перпендикулярен лучам и переносится параллельно вдоль них; амплитуда поля определяется законом сохранения эл.-магн. энергии в соответствии с адиабатич. постоянным числом фотонов в каждой лучевой трубке. В результате свет и радиоволны, напр. от звёзд или квазаров, проходя вблизи массивных тел, напр. галактик или чёрных дыр, испытывают угл. отклонение (рефракцию) и временное запаздывание. Эти эффекты, независимые от поляризации, впервые наблюдались в поле тяжести Солнца соответственно путём оптич. наблюдений затменных звёзд в 1919 [А. Эддингтон (A. Eddington)] и путём радиолокации Меркурия в 1968 И. Шапиро (I. Shapiro); в 1979-80 Д. Уолш (D. Walsh), Р. Вейман (R. Weymann) и др. обнаружили также двойные изображения квазаров, обусловленные эффектом гравитац. линзы (см. Гравитационная фокусировка). Кроме того, имеется изменение локально измеряемых поляризации и длины волны l излучения. Последнее в статич. поле тяжести подчиняется закону 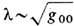и в земных условиях впервые измерено в 1960 для у-лучей с использованием Мёссбауэра эффекта[Р. Паунд (R. Pound), Дж. Ребка младший (G. Rebka Jr.)]. Вследствие расширения Вселенной существует ещё космологич. красное смещение, благодаря к-рому сдвигаются наблюдаемые спектры далёких галактик и квазаров и происходит остывание реликтового излучения.

В общем случае в соответствии с принципами термодинамики хаотич. эл.-магн. поле в вакууме, находящееся в тепловом равновесии с окружающими телами, обладающими определённой темп-рой Т, или изолированное после такого равновесного контакта, полностью характеризуется этой темп-рой и занимаемым им объёмом. Спектральная интенсивность такого равновесного, черно-тельного излучения подчиняется Планка закону излучения и в отсутствие поля тяжести не зависит от координат. В искривлённом пространстве-времени его интенсивность изменяется, становится неоднородной. Более того, как показал В. Унру [(W. Unruh), 1976], рассматривая для простоты однородное поле тяжести (или, что эквивалентно, равномерно ускоренную систему отсчёта, движущуюся с ускорением а относительно инерциальной системы), наинизшее энергетич. состояние (нулевые колебания) эл.-магн. поля там обладает ненулевой темп-рой Т _а=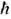a/(2pck )(в земном поле тяжести Т _а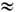4^.10^-20 К). Такую же мин. темп-ру Т _а приобретает любое пробное тело, приведённое в тепловой контакт с излучением вакуума. С указанными тепловыми свойствами вакуума в ускоренной системе отсчёта связан, напр., известный эффект деполяризации электронного пучка в магн. поле накопительного кольца [Дж. Белл (J. Bell), Дж. Лейнаас (J. Leinaas), 1983 ], описанный ранее А. А. Соколовым и И. М. Терновым (1963) в инерциальной системе отсчёта. При испарении чёрной дыры с массой M₀ и поверхностной "напряжённостью" гравитационного поля a₀ = GM₀/r _чд = c⁴/4GM₀. соответствующая чернотельная темп-pa, измеряемая наблюдателем на бесконечности, T _чд=c³/(8pGkM₀ )и по Вина закону смещения отвечает характерной длине волны l порядка гравитационного радиуса r _чд = 2GМ₀/ с² [С. Хокинг (S. Hawking), 1974]. Квантовые свойства эл.-магн. излучения в его собств. гравитац. поле ставят также абс. предел и максимально достижимой темп-ры T* = m*c²/k~10³² К, отвечающей характерной длине волны l*~L*=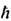/т*с, 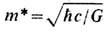где -планковская масса (А. Д. Сахаров, 1966).

Электрон-позитронный вакуум. В классич. гравитац. поле, как и во внеш. эл.-магн. поле, эл.-магн. взаимодействие меняется также вследствие неустранимой поляризации электрон-позитронных пар физ. вакуума. Последняя возникает за счёт приливного эффекта, т. е. разности сил тяжести, растягивающей электрон и позитрон в парах, имеющих виртуальный размер порядка комптоновского 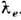. Это явление, квантовое в своей основе, видоизменяет ур-ния Э. (6 ")-(8 "). Для перем. гравитац. полей с характерной частотой 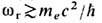и масштабом 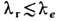оно может приводить к эфф. рождению пар реальных зарядов (электронов и позитронов) и поглощению эл.-магн. волн, напр. в ранней Вселенной или в окрестности чёрных мини-дыр. Для более плавных в пространстве-времени гравитац. полей с характерным масштабом 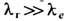поляризация пар в осн. является виртуальной, но она вполне классич. образом влияет на эл.-магн. волны [И. Драммонд (1. Drumraond), С. Хатрел (S. Hathrell), 1980]. Именно, при неизменном втором ур-нии в (8 ") первое ур-ние приобретает дополнит. слагаемые, пропорциональные производным от разл. произведений нормированного тензора кривизны 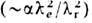на тензор эл.-магн. поля (F^ab). Для эл.-магн. волн с длинами l в интервале 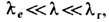не испытывающих поглощения в вакууме, но допускающих применение геом. оптики, обнаруживается, что в зависимости от поляризации и направления распространения их скорость (фазовая и групповая) может быть как меньше, так и больше "обычной скорости света" с на величину 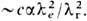Классич. принцип причинности и второй постулат спец. теории относительности этим не нарушаются ввиду неоднородности и анизотропии самого вакуума, обусловливающего взаимную неинерциальность соседствующих наблюдателей.

Согласно (16), вследствие поляризации вакуума в квазиоднородных эл.-магн. полях Е, В<< Е _c = В _c смасштабами l~ с/w>>m _е с²/е(Е+В), векторы индукции D и В в (22)

приобретают ещё дополнит. слагаемые электрич. поляризации Р и намагниченности М:

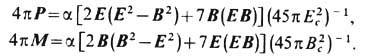
Поэтому даже в плоском пространстве-времени распространение света с волновым вектором k под углом q к однородному магн. полю В₀ сопровождается двойным лучепреломлением- фазовая скорость волн u ^ф = w/k зависит от их поляризации (направления Е):

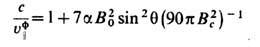
[ Е параллельно плоскости (k, B₀)];

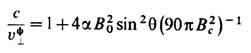
[ Е перпендикулярно плоскости (k, B₀)], если

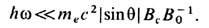
В таком намагниченном вакууме происходят параметрич. взаимодействие и распад волн (фотонов), образование гармоник, простых и ударных волн [С. Адлер (S. Adler), 1970; В. В. Железняков, А. Л. Фабрикант, 1982], а при движении зарядов наряду с магнитотормозным излучением возникают Черенкова - Вавилова излучение и переходное излучение[Т. Эрбер (Т. Erber), 1976; В. Л. Гинзбург, В. Н. Цытович, 1978]. При наличии реальной среды, напр. плазмы, многообразие явлений генерации излучения, пространственно-временной дисперсии и нелинейности волн значительно возрастает. Отметим, что многие имеющиеся здесь теоре-тич. предсказания Э. (особенно в задачах астрофизики), напр. коллективная аннигиляция сгустков электрон-пози-тронной плазмы с образованием когерентного g-излуче-ния, пока являются весьма экзотическими с точки зрения их наблюдательной проверки.

Макроскопическая электродинамика

С общих позиций Э. случай электрон-позитронного вакуума и даже плазмы во внеш. полях является не более чем характерным примером среды. В общем случае при наличии большого числа заряж. частиц (связанных или нет), возможность описания движения каждой из к-рых ограничена, хотя бы в силу квантово-статистич. законов, ур-ния Максвелла представляются стохастическими, описывающими эл.-магн. поля как случайные ф-ции координат и времени. Стохастическими являются и ур-ния движения вещества (зарядов среды), в частности материальные соотношения, характеризующие отклик на эл.-магн. поле, т. е. представляющие плотность тока как функционал поля: 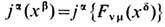. Последний может быть нелинейным и нелокальным (интегродифференциальным) и, вообще говоря, определяется независимыми от Э. закономерностями устройства среды.

Макроскопические уравнения. Флуктуации обычно отходят на второй план при наличии достаточно большого кол-ва однотипных частиц на масштабе изменения поля. Тогда без существенных потерь информации об эл.-магн. процессах можно провести квантово-статистич. усреднение ур-ний (6), (7) (без магн. зарядов) и материальных соотношений, записав их как ур-ния макроскопич. электродинамики Для средних полей и токов:

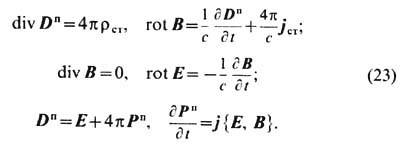
На резких границах раздела в среде необходимы граничные условия для нормальных (n) и тангенциальных (t) компонент полей

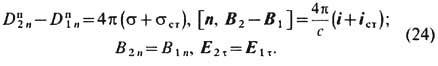
Они вместе с выражениями для поверхностных плотности заряда а и тока i через j получаются из (23) предельным переходом (n -нормаль к границе раздела, направленная из первой во вторую часть среды). Здесь для определённости пространство-время предполагается плоским, а вакуум- однородным и изотропным, используется инерци-альная система отсчёта, к.-л. образом связанная со средой в целом. Все свойства среды, за исключением сторонних зарядов r _ст и токов j _ст, включены в новое поле электрич. индукции D ^п(t, r)[или полной электрич. поляризации P ^п(t, r)] и задаются функционалом j { Е, В}. В линейной Э. соответствующее материальное ур-ние имеет вид

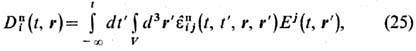
учитывающий временную (частотную) и пространственную дисперсии, т. е. запаздывание и нелокальность эл.-магн. отклика среды (см. Диспергирующая среда). Эти явления обязаны, напр., собственным молекулярным колебаниям и конечности межатомных расстояний в твёрдом теле или длины свободного пробега ионов и электронов в плазме. Система (23)-(25) обладает полнотой, позволяя однозначно определить поля в любой области среды V, если для них заданы необходимые начальные и граничные условия; для учёта влияния среды вне рассматриваемой области V на процессы внутри неё на её границе 2 требуется ставить нелокальные, интегральные условия.

При таком подходе макроскопич. поля и движение отд. частиц среды выпадают из рассмотрения. Так, в отсутствие дисперсии, согласно Ома закону jⁱ =s^ilE_l , плотность тока в проводнике при учёте только свободных зарядов полностью определяется тензором его проводимости s^il и средним электрич. полем E_l . В соответствии с этим иногда делают дополнит. приближения. Скажем, в электростатике поле внутри проводника считается равным нулю, а свободные заряды - сосредоточенными только на его поверхности, хотя в действительности они отличны от нуля, по крайней мере в тонком поверхностном слое. Аналогично в магнитостатике сверхпроводников 1-го рода вследствие Мепснера эффекта предполагается невозможным существование объёмных внутренних плотностей тока и магн. поля, хотя они заведомо имеются в поверхностном слое конечной толщины (см. также Скин-эффект, Леонтовича граничное условие). Подобные дополнит. приближения не обязательны, поскольку ур-ния (23) позволяют учесть сколь угодно резкие изменения полей в пространстве и во времени, если в них не проведено усреднение по физически бесконечно малым объёму и интервалу времени. Последняя операция, часто используемая со времён Лоренца (1902), ведёт к более грубому пренебрежению флуктуаци-ями, чем статистич. усреднение, и может ограничивать возможности анализа пространственной и частотной дисперсии сред, напр. динамики поверхностных поляритонов. Что касается возможного отличия действующего на заряды поля Е_g от среднего Е (т. н. поправки Лоренца, равной, напр., Е_g - Е=4p Р ^п/3в кубич. кристалле или в газе нейтральных молекул), то в обоих способах усреднения оно предполагается принятым во внимание при микроскопия, выводе материальных соотношений благодаря учёту корреляций взаимного расположения частиц и их взаимной непроницаемости.

Дисперсионные и энергетические соотношения. В стационарной однородной среде удобно перейти к фурье-образам полей, получая, в частности, из (25)

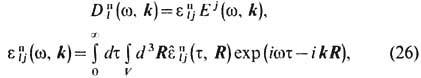
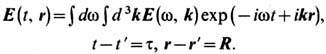
Полный тензор диэлектрической проницаемостиe ^п_lj учитывает не только электрич., но и магн. свойства среды, т. е. влияние индукции В на D ^п. Он обладает определ. свойствами симметрии (см., напр., Анизотропная среда, Гиpo-тропная среда), а также аналитичности - как комплексная ф-ция своих комплексных аргументов w и k. Напр., согласно принципу причинности в устойчивой, в частности равновесной, среде при k0 тензор e ^п_lj(w, k0) не имеет полюсов в верх. полуплоскости lmw>=0 для диэлектриков, имеет простой полюс 1/w для проводников и полюс второго порядка 1/w² для сверхпроводников. При k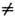0 сказанное заведомо справедливо лишь в отношении обратного тензора (e ^п_lj)^-1 (w, k), связывающего поле Е с вызывающей его индукцией D ^п, к-рой можно независимо, в отличие от Е, управлять путём изменения внеш. зарядов r _ст(t, r) (Д. А. Киржниц, 1976). Отсюда можно прийти к дисперсионным соотношениям, связывающим вещественную и мнимую части e ^п_lj(w, k0) [или (e ^п_lj)^-1(w, k)]. Существуют и др. феноменологич. соотношения и ограничения на возможный вид тензора проницаемости. Так, поскольку для монохроматич. волны E=Re [ Е₀ ехр (- iwt + ikr)]. свещественными w и k тепловая энергия, выделяющаяся в единице объёма за единицу времени ( джоулееы потери), равна Q ^п = (w/8p) [Ime ^п_lj(w, k)]^.E ^j₀E*^l₀, то в равновесной среде в соответствии с принципом возрастания энтропии должно быть Q ^п>0 (при w>>0) для любого комплексного Е₀,

Справедливость указанного определения Q ^п в условиях изменения общей энергии среды и поля за счёт работы сторонних источников становится ясной, если усреднить по достаточно большим объёмам и интервалам времени вытекающее из (23) соотношение Пойнтинга:

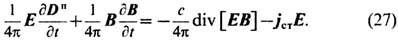
Без микроскопич. анализа энергетич. смысл членов в (27) для диссипативной среды является, вообще говоря, неоднозначным. Лишь в прозрачной среде для квазимоно-хроматич. пакета однородных волн можно заранее указать ср. плотность энергии и её поток, а также групповую скорость волн u _гp = S/w[Л. Бриллюэн (L. Brillouin), 1921; М. Е. Герценштейн, 1954]

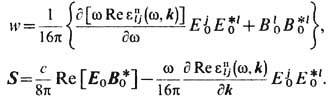
При этом даже в однородной изотропной немагнитной среде без пространственной дисперсии, когда D ^п₀ = e ^п(w)E₀, на единицу объёма среды действуют не только сила Лоренца со стороны внеш. зарядов и токов и по-ндеромоторная сила, связанная с пространственной неоднородностью полей, но ещё и т. н. сила Абрагама (см. также Максвелла тензор натяжений), обусловленная нестационарностью полей,

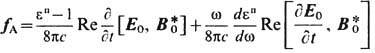
(X. Вашини, В. И. Карпман, 1976).

Поляритоны (светоэкситоны). При учёте пространственной дисперсии в ур-ниях Максвелла для фурье-образов полей при замене (25) на (26) необходимо указать ещё дополнит. граничные условия, обусловливаемые физ. свойствами поверхности среды (С. И. Пекар, 1957; В. Л. Гинзбург, 1958) (см. Кристаллооптика). Эти условия определяют, в частности, эффективность возбуждения в ней разл. нормальных волн (поляритонов), в т. ч. поперечных (E | k )и продольных (E||k, D = B =0)(см. Плазмон). Дисперсия k _а = k_a(w) или w_a= w_a(k), а также поляризация E_a(k )и групповая скорость u _гр=dw_aldk всех этих волн ( а=1, 2, 3, ...), согласно (23), находятся из однородной системы алгебраических ур-ний [w² с~²e ^п_lj(w, k) - -k²d_ij + k_ik_j]E ^j(w,k) =0. Для решения разл. задач, напр. об излучении сторонних источников или о развитии неустойчивости волн в неравновесной среде, широко применяется т. н. гамильтонов метод анализа поля излучения, основанный на его разложении по нормальным волнам (В. Л. Гинзбург, 1940).

Без учёта пространственной дисперсии, т. е. зависимости e ^п_lj от волнового вектора k, при решении граничной задачи остаются, как и в вакууме, только две, различающиеся поляризациями Е_{0, е} , обыкновенная ( а = о )и необыкновенная ( а = е )волны k_{0, e}(w) (см. Френеля уравнение), а также продольные колебания на дискретных частотах, для к-рых dete ^п_lj(w_||)=0. При решении начальной задачи имеющаяся частотная дисперсия e ^п_lj(w) сказывается более явно и поэтому даже в изотропной среде благодаря поляризац. вырождению k₀(w) = k_e(w)может быть неск. дисперсионных кривых w _а(k )-в соответствии с числом разл. свободных самосогласованных колебаний зарядов среды и поля с заданными волновым k и поляризационным Е векторами. На рис. 3 приведён схематич. вид спектра нормальных волн в случае материального соотношения

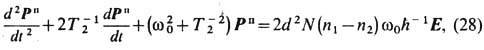
отвечающего модели изотропной среды практически неподвижных молекул с двумя энергетич. состояниями 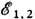, , 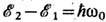их населённостями п₁ и n₂, концентрацией N, электрич. дипольным моментом перехода d с временем некогерентной релаксации Т₂. Модель (28) лежит в основе квантовой электроники: при инверсии населённостей (n₁ <п₂ )активных энергетич. уровней молекул образца среды в зависимости от скоростей релаксации поляризации Р ^п и поля Е возникает неустойчивость одной из двух волн w_1,2(k), ведущая к мазерной генерации (Imw₁>0; см. Лазер )либо к сверхизлучению Дикке (R. Dicke) (Im w₂>0).

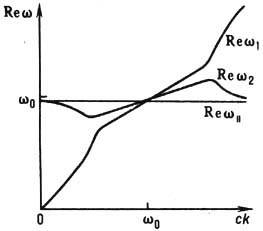
Рис. 3. Качественный вид дисперсионных кривых нормальных волн в среде, состоящей из двухуровневых молекул - осцилляторов.

Магнитная и электрическая восприимчивости. В Э. сплошных сред часто используется отличная от (23), более симметричная форма ур-ний. Она основана на выделении тока проводимости "свободных" зарядов j₀ (посредством введения к.-л. тензора проводимости) и намагниченности М', позволяющей ввести новый вектор напряжённости магн. поля H(t, r) = В-4p М' и новые тензоры магнитной проницаемости 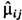(t, t', r, r' )и m_ij(w, k), играющие в ф-лах вида (25), (26) роль, аналогичную вектору Е и переопределённым тензорам 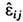и e_ij соответственно. В результате полная плотность тока разлагается на 3 части: j{E,B}=j₀ + crotM' + д P'/дt, а индукция магн. поля В становится аналогичной вновь переопределённой индукции электрич. поля D=E+4pP', выражающейся через "оставшуюся" поляризацию Р' (электрич. дипольный момент единицы объёма).

В условиях пространственной дисперсии среды, не говоря уже об её нелинейности, макроскопич. процедура выделения j₀, М', Р' и введения новых 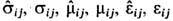по старым 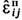, e ^п_ij неоднозначна. Это обстоятельство обуслов-лено невозможностью строго разделить замкнутые и незамкнутые токи или токи "свободных" и "связанных" зарядов, особенно для эл.-магн. полей с характерными масштабами, к-рые не могут считаться большими по сравнению с размерами области локализации "связанных" зарядов, напр. электронов в молекулах. Причиной неоднозначности может служить релятивистская взаимосвязь Р' с М' или Р' с j₀, скажем, в многокомпонентной среде при наличии неск. потоков зарядов в каждом элементарном объёме dV. Даже в простейшем случае непроводящей изотропной (негиротропной и немагнитоактивной) линейной однородной стационарной среды, где общее выражение для полной проницаемости суть

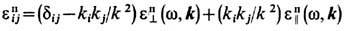
(e_| и e_|| -диэлектрич. проницаемости среды соответственно в случаях, когда Е перпендикулярно и параллельно k), связь прежних фурье-образов D ^п_i =e ^п_ijE ^j можно заменить, напр., на две эквивалентные пары новых связей (А. М. Игнатов, А. А. Рухадзе, 1981):

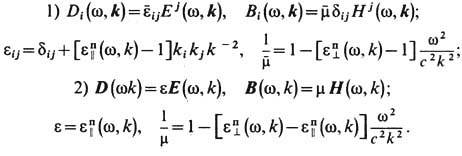
Тем не менее в известных приближениях определённое разделение удаётся провести либо из микроскопич. соображений, либо за счёт дополнит. условий в к.-л. частных случаях.

Движущиеся среды. Для указанного разложения j {E, В} ур-ния (23) принимают вид

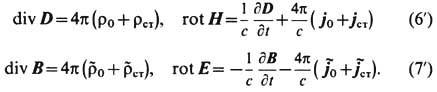
В ( Т )включены ещё эфф. магн. заряды и токи, иногда используемые, напр., для удовлетворения определ. граничным условиям при описании свойств неоднородных сред или при переходе во вращающуюся систему отсчёта с целью отыскания решений граничных задач путём применения двойственности перестановочной принципа (преобразований дуальности Лармора - Пистолькорса), обобщающего (10) на случай макроскопич. Э. Ур-ния (6'), (7') сохраняют свой вид при переходе в произвольную инерци-альную систему отсчёта (относительно к-рой среда равномерно движется с локальной скоростью и), если учесть релятивистские преобразования токов j^a₀, j^a _ст,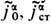и полей (2). Поля D и Н преобразуются аналогично полям Е и В соответственно и образуют тензор индукции Н_ab, аналогичный F_ab (Г). Поэтому ур-ниям (6'), (7') можно придать релятивистски ковариантную форму:

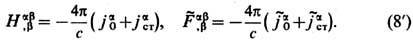
Однако в общем случае, в отличие от силы Лоренца в вакууме (1') или (11), заменяющие её материальные соотношения не обладают релятивистской ковариантностью, поскольку явно выделена локально инерциальная система отсчёта, связанная со средой. Ситуация упрощается в среде без пространственно-временной дисперсии, имеющей вещественные проницаемости и проводимости, для простоты предполагающиеся изотропными в этой системе отсчёта:

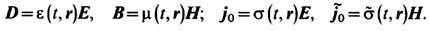
В произвольной системе отсчёта эти материальные соотношения принимают вид [Г. Минковский (G. Minkowski), 1908]

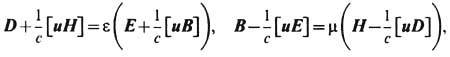
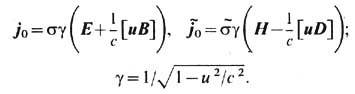
Их явная ковариантность устанавливается эквивалентной формой записи (И. Е. Тамм, 1924; М. И. Рязанов, 1957; Б. М. Болотовский, С. Н. Столяров, 1977)

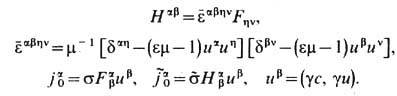
Соответствующим образом меняются и граничные условия (24). Напр., в отсутствие поверхностных зарядов и токов на границе раздела сред, движущейся с локальной скоростью u', наряду с нормальными компонентами индукций D, В должны быть непрерывны тангенциальные компоненты векторов

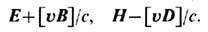
Электромагнитные взаимодействия в среде. Неоднородное движение среды или движение одних элементов среды относительно других нарушает её изотропию и равновесность, делает возможными неустойчивость и усиление эл.-магн. волн за счёт кинетич. энергии вещества (см., напр., Неустойчивости плазмы), видоизменяет потенциалы Лье-нара - Вихерта, в частности кулоновское поле покоящегося заряда, а при наличии временной дисперсии частично переводит её в пространственную (и наоборот). Уже в покоящейся среде собственное поле и поле излучения к.-л. источников, напр. движущихся заряж. частиц, могут качественно отличаться от поля в вакууме, даже если отвлечься от их непосредств. столкновений с частицами среды, вызывающих искривление траекторий, ионизац. потери и др. Дело в том, что наряду с колебаниями эл.-магн. поля неизбежно должны возбуждаться самосогласованные колебания зарядов в среде; в частности, излучаться могут только нормальные волны. Так, на тормозное излучение, эл.-магн. массу, эфф. заряд и радиац. трение быстрой частицы принципиально влияет вызываемая её движением переполяризация среды (Э. Ферми, 1940). Эти явления наблюдаются, напр., при каналировании заряженных частиц в кристаллах или в газах. Обнаруживаются возможности Черенкова - Вавилова излучения, переходного излучения и ондуляторного излучения, аномального Доплера эффекта и др. особенности излучения монопольных, дипольных и мультипольных конфигураций зарядов. Изменяется характер распространения излучения, в т. ч. геом. оптика и дифракция, особенно в нестационарной и неоднородной среде. В результате меняется эффективность взаимодействия зарядов.

Ситуация может усложняться нелинейными свойствами эл.-магн. волн и их взаимодействий с частицами, а также разл. процессами рассеяния на упругих, тепловых и др. неэлектромагн. возбуждениях среды. Скажем, возможно нелинейное черепковское излучение под действием короткого импульса сильного эл.-магн. поля, возбуждающего на своём пути нелинейную поляризацию среды в отсутствие к.-л. сторонних зарядов и токов (см. также Электродинамика движущихся сред).

Лит.: Ландау Л. Д., Лифшиц Е. М., Теоретическая физика, т. 2, 4, 8, М., 1980-89; Джексон Дж., Классическая электродинамика, пер. с англ., М., 1965; Агранович В. М., Гинзбург В. Л., Кристаллооптика с учетом пространственной дисперсии и теория экситонов, 2 изд., М., 1979; Вейнберг С., Гравитация и космология, пер. с англ., М., 1975; Стражев В. И., Томиль-чик Л. М., Электродинамика с магнитным зарядом, Минск, 1975; Гинзбург В. Л., Теоретическая физика и астрофизика, 3 изд., М., 1987; Гроот С. Р. де, Сатторп Л. Г., Электродинамика, пер. с англ., М., 1982; Туров Е. А., Материальные уравнения электродинамики, М., 1983; Железняков В. В., Кочаровский В. В., Кочаровский Вл. В., Волны поляризации и сверхизлучение в активных средах, "УФН", 1989, т. 159, с. 193.

В. В. Кочаровский, Вл. В. Кочаровский.